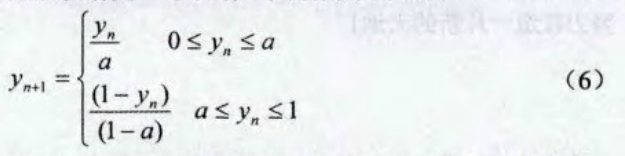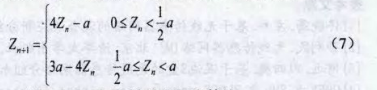近几年混沌理论越来越多的应用于加密领域,其本身的特性更适合资源受限的无线传感器网络.本文提出了一种基于Kent映射和Logistic映射的混合混沌系统,并采用适合无线传感器网络的基于Feistel网络结构的分组加密算法。
一、混沌加密理论
1、logistic映射及其整型数值研究
Logistic映射是一维离散动态系统,其动力学方程为:
其中,Xn+l是第n+l次的迭代值,μ是系统参数,X0是第n次的迭代值。
Logistic映射在值域上是连续的,并不适用于WSN。
对上式存在一种等价的方式:
其中,xn∈[-i,l],入∈[O,2],将式(2)两边同时乘上a2 (a≠0),得到:
令zn=axn+a,则:
取入=2,化简即得:
Xn∈[-1,1[,zn∈[o,2a],a=2L-l,L为机器字长。
2、Kent映射及其整型化数值研究
Kent映射是一维映射,其动力学方程为:
式中,yn∈[0,I]是序列值:a∈(0,1)是分叉参数,当a=0.4997时,Kent映射呈现最佳状态。整数化后如下:
二、基于Feistel网络的分组加密算法
1、Feistel函数的内部结构
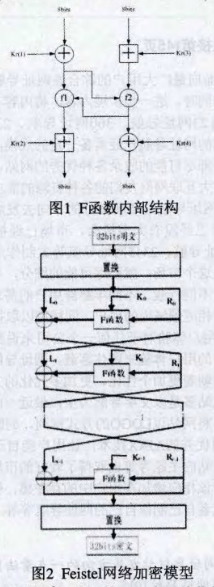
在Feistel网络结构中,F函数是其最核心的部件,它越复杂加密性越好。
图l中的⊕表示模28加法运算,⊕表示按位异或,函数fl,f2分别表示整型数值化的Kent映射方程式和logistic映射方程式,Kr (t)代表第r轮加密子密钥分量。
2、加解密过程
设一个Feistel网络结构加密算法,轮函数作用R次,分组长度为2n,那么每轮的操作可定义为:
Roundi: LiiIRi-RiIIF (Ki,Ri)⊕Li,其中i=O,1,2,…,r,Li和Ri为分组长度相等的左右两个部分,Ki为“1轮使用的加密子密钥。
图2为32bit分组加密过程。在明文分组进入Feistel加密网络之前,先对数据进行P置换,再将明文分组分为Li和Ri,迭代后得到32bit输出再逆P置换作为加密结果。其加密与解密过程结构相同。
3、安全性能分析
设计分组密码体系要遵循混淆和扩散两个基本原则。混合混沌映射能得到良好的扩散和混淆特性,相较于S盒的混沌加密算法,既提高了加密速度,又节省了存储空间。此外,混合后的混沌映射能够抵抗差分分析攻击,运行效率也得到提高。
小知识之Feistel
在密码学研究中,Feistel 密码结构是用于分组密码中的一种对称结构。