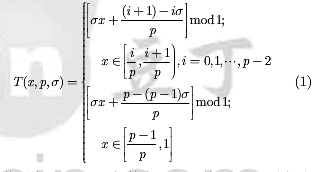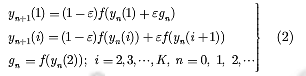图像加密算法之Markov分割 - 夏冰加密软件技术博客

为了设计复杂度高、安全性好而计算代价小的图像密码算法，我们从一类新的具有Markov分割性质的混沌系统出发构造了此算法。

一、混沌系统构造

1、可Markov分割的混沌系统的特性

本文使用一种可Markov分割的混沌系，简单描述如下：选取参数p（p≥7）是素数，将[0，1]区间p等分，构造映射T(x，p，σ)如式(1)，其中σ∈Z+且2<σ≤p -1。

其平均Lyapunov指数为In（σ），其Markov分割为i1,i2，...，I，其中Ik=[(k - 1)/p,k/p]，σ=l,2，…，p。

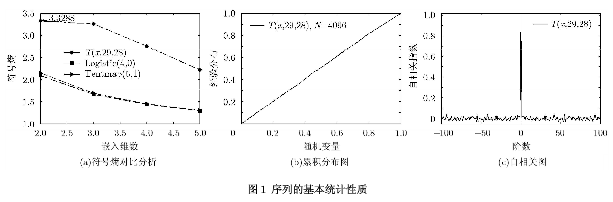
此系统产生的序列有着比较好的统计性质：其极限分布为均匀分布，自相关函数近似为6函数，为一个理想的均匀伪随机序列。而通过对其复杂度分析可知，通过参数调整它具有比Logistic映射和帐篷映射高得多的复杂度，其符号熵对比分析结果如图1(a)所示。

2、随机选取初始点(xo =1/23)迭代4096次实验，其均匀性和相关性如图1(b)和图1(c)所示。从图1(b)可知，其累计分布函数类似一条直线，这意味着其概率密度函数近似于常数，即为均匀分布。通过Kolmogorov-Smirnov统计检验得p值为pl_KS=0.9590，通过Chi-square拟合优度检验得p值为p1_CHI2=0.9597，可以认为此系统产生的序列服从均匀分布。而对序列的相关分析如图3(c)所示，其接近于一个6函数，为一个理想的伪随机序列。

2、改进时空混沌系统

低维的混沌系统因密钥空间限制和相空间结构简单而可能产生安全漏洞，这可以利用时空混沌系统来解决，其中最常用的是耦合格子映射。一个K阶的单向发展的耦合格子映射如式(2)，可掩盖系统的相空间结构，其常用于密码系统的设计，其结构表示如式(2)。

边缘条件满足yn(K+1)=yn(1)，gn表示耦合格子映射的输出，K表示系统耦合的阶数，g表示为耦合轨道分配的权重函数，为基本的混沌系统，因其产生的序列非均匀分布，用于密码设计不够理想这里用上述的混沌系统T(x，p，σ)来代替。(yo(1)，y0(2)，…，y0(K))表示耦合格子系统的初始值，可用做混沌密码系统的初始密钥。

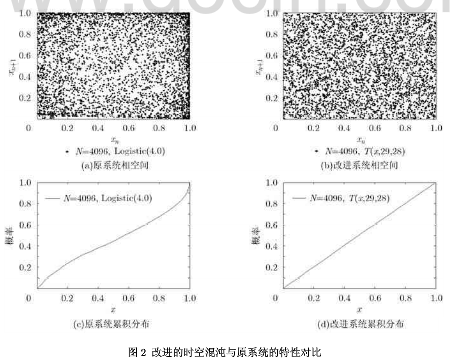
选取系统参数为k=6，权重ε=0.99初始值为(0.9/6, 1.9/6, 2.9/6, 3.9/6, 4.9/6, 5.9/6),迭代4096次后测试结果如图2所示。通过耦合格子映射变换后的混沌系统的相空间如图2(a)和图2(b)所示已无规律可循，由图中可以看出，原系统的相空间分布在边缘位置较稠密而中间偏稀疏，而改进后的系统其分布明显好于原系统。然后，对改进的系统测试其累积分布，与原系统的对比如图2(c)和图2(d)所示，可见改进系统其累积分布更接近均匀分布，因而更适合用于密码算法的设计。

二、图像加密算法构造

1、加密算法框架

1、算法框架

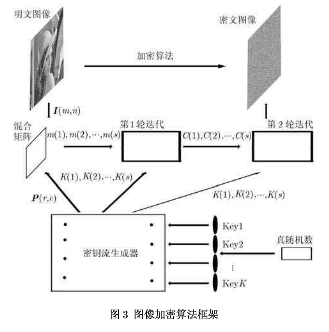
分析了上述加耦合格子映射的混沌系统性质后，利用其产生的序列生成密钥流，根据密钥流生成动态置乱矩阵，对图像像素位置进行置乱，然后利用迭代加密模块对像素数值进行替换。该图像密码算法分为3个部分：密钥生成算法，加密算法和解密算法。其加密过程如图3所示。

2、密钥流生成算法

步骤1 选择混沌系统参数p（为素数）和σ(sigma)，耦合格子系统阶数K(dim)和耦合轨道分配的权重e。

步骤2 根据耦合格子系统阶数K选择迭代系统初始值为(XI，X2，xk)，密钥为(xl，X2，…，Xk)，此处xt(t=1，…，K)仅表示与Xt(t=1，m，K)区别，无特殊意义。然后通过[0，1]上均匀分布的真随机数RND(其生成方式已有不少扰动密钥，生成迭代初始值X=xi+RND(i=L 2，…，K)。引入真随机数可达到一次一密的效果。迭代过程中产生的密钥流需要量化为字节流kn= floor(gL×256)。

步骤3根据输入的明文图像尺寸S(M×N)生成密钥流的长度/-2×M×Ⅳ，记为向，砭，…，kL。其中KLi =(ki,k2，…，kLi(Pi,p：，…，p/i)(/i=M×Ⅳ-1)用于消除系统初始迭代时的震荡和构造置换矩阵，舍弃前16个数值，然后依次产生M个和N个不同的整数序列构成两个置换PM和PN广将生成的置换矩阵记为P他(，)= PMoPN(J)。后半部分密钥记为Kj:2 =(kLi+I，kLi+2，…，kL)=(kl，k2，…，kn)，直接用于加密图像的迭代操作。

3、加密步骤

步骤1初始明文图像记为J= (Iij)MxN，置换操作后的图像为P= (Pij)M×Ⅳ=P(J)。将置换后的图像记为数据流的形式即为(mi，7712，…，mt，…，m。)，其中mt=Pij，t=（i-1）×M+n，1<t<s。

步骤2将生成的数据流依次输入两轮迭代系统表示如式(3)和式(4)，经过此两轮操作后产生的密文为(Di，D2，…，Dt，…，Ds)。这里的CO为迭代系统的启动参数，它作为密钥由密钥文件提供。

4、解密步骤

该图像密码算法为对称密码算法，所用解密密钥同加密密钥一致，密钥生成算法同上，此处真随机数与加密过程所用保持一致。

5、密钥文件

上述算法所用的密钥文件如表所示，主要有4个部分构成，混沌系统参数、耦合格子映射参数，加密系统启动参数和真随机数。其中参数(p，sigma，dim，e)这4个参数变动范围比较小，密钥空间的大小主要靠(XI，X2，…，Xdim)和RND来提高，以dim-6为例，在32位系统中，密钥长度即可达到192 bit，再加上产生的真随机数C也是32 bit，系统的密钥长度可达224 bit。该图像加密算法对密钥的变化非常敏感，这可由后文的密钥敏感性测试看出。系统密钥文件的参数和功能如表1所示。