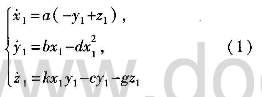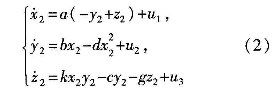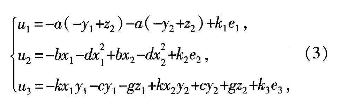混沌反控制为混沌控制的一个研究方向,已成为人们研究的热点。为此,我们今天就来探讨一下图像文件加密中混沌反控制的应用。
一、混沌与混沌反控制概念
混沌是非线性系统中的非线性运动,它的运动轨迹类似于随机运动,但又不完全随机,混沌对系统初始条件及系统参考极其敏感,混沌运动的相空间轨道有界,有正的李雅普诺夫指数,有限的kolmogorov-Si-nai嫡,类连续的功率谱,伴有分叉和分形现象等。
最开始人们认为混沌是有害的,如混沌会对机电系统或电路系统产生不规则的震荡,需要消除或者削弱混沌现象,于是提出了很多混沌控制的概念和理论,这种控制称之为混沌控制,即混沌正向控制,简称为混沌控制。但是后来人们发现,混沌并不只是有害的,比如在保密通信系统等应用领域中混沌是有益的,于是人们希望产生混沌,或者将混沌进行强化,即混沌的反向控制(简称为混沌反控制),于是混沌反控制成为了人们研究的热点。
二、混沌反控制常用的方法
对于任意的一个系统,可以是混沌的,也可以是稳定的,可以是线性的,也可以是非线性的,可是时为的,也可是时不变的,混沌反控制的目标是设计一控制器将系统产生混沌或者强化一个混沌系统的已有混沌运动。在对混沌反控制的研究与探索过程中,很多专家学者提出了很多混沌反控制的研究方法。可归纳总结为:利用混沌系统本身的特性、改变已有混沌系统混沌吸引子的方法、采用线性或非线性的外力作用、使用跟踪系统状态的方法来实现混沌反控制,实现混沌反控制的具体方法如下。
1、将线性或非线性作用施加到受控系统
混沌是非线性系统中的一种非线性运动,对非线性系统施加线性的或非线性的状态反馈作用,使原有的非线性系统混沌化或者原有的非线性系统混沌信号加强,这是目前应用最广泛的一种强化混沌的混沌反控制方法。
2、设置李雅普诺夫指数大于0
非线性系统的李雅普诺夫指数大于0时,系统呈混沌状态。因而将离散非线性系统的李雅普诺夫指数配置大于O时,系统会混沌化,李雅普诺夫指数即适合高阶系统,又适合低价系统,但是李雅普诺夫指数的求取非常困难,尤其是在外界干扰和系统结果及参数不完全清楚时,更加难以计算,因此通过设置李雅普诺夫指数大于O使系统混沌化实现混沌反控制的方法应用范围小。
3、附加时滞反馈控制
含时滞的动力学系统属于无穷维系统,能产生复杂的动力学行为,通过对受控连续系统进行参数扰动和对受控系统引入状态时滞反馈输入,对稳定的线性方程实现时滞反馈混沌反控制.这种反控制方法所引入的外加扰动很小,因而此类方法应用较广。
另外,对已有混沌系统的混沌吸引子进行变异,通过受控系统状态对已知混沌系统状态跟踪等混沌反控制研究方法也获得了较好的研究成果。
三、线性混沌反控制系统
1、非线性系统模型
有资料提出了如式(1)所示的非线性混沌系统模型:
在上式中,(X1,y2,Z1)T∈R3是该系统的状态变量,其中a,b,c,d,g,k为系统的参数,当参数取值为:a=8,b=40,c= 10/3,d=3,k=1,g=4时,式(1)为混沌系统。
2、混沌反控制方法
现假设式(1)为驱动系统,构造一个响应系统如式(2)所示:
式(2)中UI,U2,U3为所需设计的控制器,本方案中设计如下式(3)所示的控制器函数:
式(3)中,ei =xi +X2,e2 =Yi +y2,e3=Z1+22,在式(3)的作用下,当![]()
,式(1)和式( 2)两个系统实现了全局同步,即实现了混沌反控制。
四、混沌反控制系统在图像加密中的应用
假若明文图像为I,I的大小为MxN,加密后的图像,I'为了验证受控系统式(2)在控制器式(3)作用下的混沌性能,本文设计了如下的图像加密算法。
骤a:给定系统(1)和系统(2)的初值及参数值,生成长度为4000+MxN的混沌序列{ X2},{y2},{z2};
步骤b:任意选定{X2},{y2},{z2}三个序列中的一个序列并舍弃前面的4000个值,生成混沌序列{W2};
步骤c:将{W2}序列中的各个值取小数点后第9,10,11连续三位组成正整数序列,并将每个值取256的余,组成新的序列{W2‘};
步骤d:选择图像,中的第一个像素点与{W2‘}序列中的第一个值进行异合得到加密后的像素值,依此类推,直到图像I中的每个像素都进行了加密,得到图文图像I’。图像的解密过程与加密过程的逆过程。
小知识之李雅普诺夫指数
李雅普诺夫指数又叫Lyapunov指数,是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。对于系统是否存在动力学混沌, 可以从最大Lyapunov指数是否大于零非常直观的判断出来: 一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。