图像加密算法之六态量子密钥 - 夏冰加密软件技术博客

鉴于现有图像加密技术的局限性以及量子密钥分配方案的高度安全性，我们提出一种基于六态量子密钥的图像加密算法。在四态方案(BB84协议)两组共轭基的基础上，引入l对旋转测量基构成六态方案基矢空间；由六态方案产生随机的二进制密钥串，将密钥串与图像数据进行异或运算，对图像数据置换，实现图像的加密。

一、量子密钥分配协议

量子密钥分配(QKD)协议指利用量子互补、量子不可克隆和不可擦除原理，通信双方或多方在通信中将信息编码为比特，建立共享密钥的协议。密钥信息编码在单光子的偏振态上进行传输。

1、BB84方案

方案采用非正交的2对基矢，分别为光子偏振的水平垂直基“十”和对角基“x”。水平垂直基“+”中，水平偏振(0。)记作I—+>．垂直偏振(90。)记作It>;对角斜基“x”中4S。偏振记作l 7>．1350偏振记作I＼>。用0和l对两组基编码。测量基有x2种，对于对角偏振光子用“x”可得确定测量结果，对水平倔振光予用“+”基的测量结果是确定的。为了传输信息．BB84方案制备好量子态，并约定对应的编码信息，用量子信道来传输量子态。

BB84方案中，作为量子密钥的只有500/的光子。为了确保传输的安全性，检测过程中超过50%的光子将被丢弃，导致方案的量子资源利用辜较低。此外．BB84方案用4个量子态来编码“O”和“l”，编码容量较低；BB84协议受到简单个体攻击时，由于通信双方只保留基相同的信息，导致最终的误码率为25%。

2、六态QKD方案

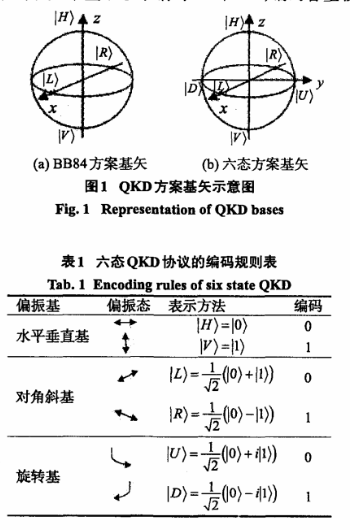
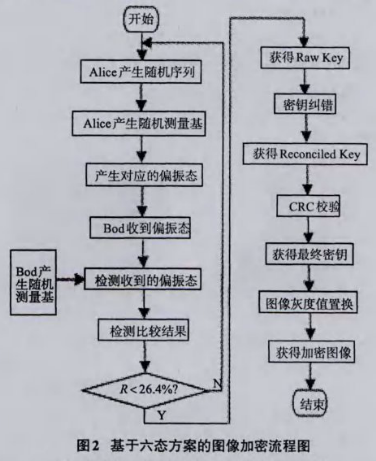
六态方案在BB84四态方案的基础上，添加一组与四态相垂直的偏正态，即选取光子6个方向的偏振态，分属3组（其中每组2个）构成基矢空间（见图1），将光子制备在偏振态上，并约定量子态代表的编码信息，从而实现量子比特的制备。图1(a)显示的是BB84方案2组基矢和4个偏振态，图l(b)为六态方案3组基矢和6个偏振态。6个偏振态分别对应于Bloch球中x，y，z方向上的6个自旋为1/2的态，每个偏振态对应的编码信息如表1。

六态方案中使用3组测量基，使得编码容量增大。设定信息发送方为Alice，接收方为Bob，Eve为窃听者。该方案的特点是Eve对同一光子选择与Alice相同测量基的几率只有1/3。由于Eve的窃听会对Bob的测量结果引入2/3 xl/2=33.3%的错误率，大于BB84方案中的25%，从而Evc的窃听行为更容易被检测。因此，相比于BB84方案，六态方案安全性进一步提高。

二、图像加密算法及其实现

1、六态QKD协议

六态QKD协议包括单向量子信道通信和双向经典信道通信，其中Alice向Bob发送初始密钥串在单向量子信道进行，密钥的校验则是在双向经典信道上进行，具体如下：

1)Alice随机产生一个二进制quantum序列（待传输），再产生一个由(O，1,2)随机组合而成的序列作为测量基矢量。产生对应的偏振态序列Bit，利用3个变量pl，p2，p3组合而成的6个序列分别表示测量基所对应的6个偏振态。其中：0对应偏振态001，010;1对应偏振态011，100；2对应偏振态101，110；

2)当Evc不存在时，Alice将编码后的光子发送给Bob，Bob产生一个由{0，1，2）组合而成的随机序列作为测量基，然后将Alice和Bob产生的测量基序列按位比较，剔除双方不一致的数据，得到Raw Key;

3)有Eve的情况下，Eve产生一个由{0，1，2）组合而成的随机序列，当Bob选择的测量基与Eve一致时，将Eve比特值赋给Bob，否则Bob接收到的为随机数；

4) Alicc与Bob从Raw Kcy中随机挑选一部分数据，进行比较，并验证是否一致，得误码率Ro如果R<26.4%(预先设定的误码率上限)，进行下一步骤；否则，回到步骤1）；

5)通过奇偶校验法和二分查找法进行密钥纠错，得到Reconciled Key;

6)通过CRC校验法对Reconciled Kcy进行校验，得到最终密钥。

2、基于六态QKD协议的图像加密

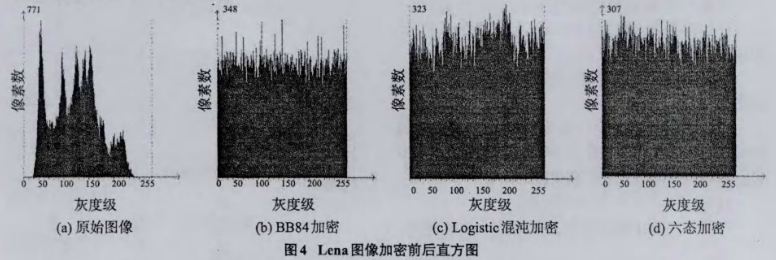
设原始图像大小为MxN，加密算法流程如图2，描述如下：

1)设定Alice端发送的量子比特数。当不存在窃听者Eve时，获得量子密钥串Q；当存在窃听时，通过误码率判断、奇偶校验法、二分查找法、CRC校验法得到最终密钥串Q；

2)读取待加密图像，并将灰度值转化为二迸制序列U；

3)当Q的长度小于U的长度时，循环使用Q直到长度相等；当Q的长度大于U的长度时，截取U长度的序列。通过此过程获得序列C；

4)对序列C和U作异或运算；

5)将结果转化成十进制，完成图像的加密过程。

三、实验结果与性能分析

实验采用VC6．O编程实现，对8位Lena灰度图像测试，并与四态、Logistic混沌加密方案等进行比较，结果见图3。其中图3(b)为基于BB84方案加密后的图像，图3(c)为基于Logistic混沌方法加密后的图像，图3(d)为基于六态量子密钥分配方案加密后的图像。

1、密钥空间分析

密钥空间是指密码系统可使用的不同密码总数。本方案将六态QKD协议产生的随机序列作为密钥的初始参数值，由于六态方案每次执行，Alice产生的二进制序列是随机的，Bob和Alice选用的测量基是随机的，得到的Raw Key也是随机的；密码系统随着执行次数的增加，可使用的密码总数随之增加，没有上限，可使密钥空间足够大，足以抵抗穷举攻击。

2、统计特性分析

（1）像素值分布特性

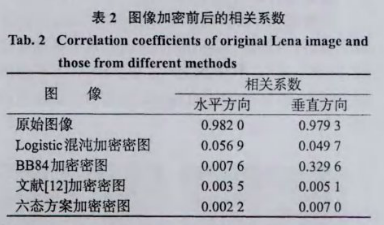
图像的像素值分布规律可由直方图反应。图4为Lena原图及由BB84(四态)、六态及Logistic混沌法加密后图像所对应的直方图。比较图嘶砂俩可以看出，像素直方图在图像加密前后有显著改变，加密后的直方图呈均匀分布，原图像中像素分布规律被掩盖。较之图4(b)、(c)，图4(d)分布更为均匀，表明基于六态方案的图像加密算法能够更好地掩盖原图像的像素分布规律，抵抗统计分析攻击能力提高。

（2）像素间相关性分析

相邻像素间相关性的大小可用相关系数rxy来度量:

其中：

x1和yl是2个相邻像素的灰度值；三是像素总数。

分别计算从加密后图中选择的水平和垂直方向相邻像素之间的相关系数，结果见表2。分析表2数据可看出，加密前图像中像素间具有强相关性，加密后像素之间相关系数很小，相关性被破坏，其中采用基于六态方案的加密方法所得的加密后图像像素相关度系数最小。由此表明，栩较于BB84方法、Logistic混沌加密方法，六态加密方法能够较好地掩盖原图像的像素规律，抵抗统计攻击能力增强。

（3）灰度变化平均值分析

图像加密后，大部分像素的灰度值会发生变化。当图像加密前后的灰度值均匀变化时，加密图像的安全性较高。灰度变化平均值ga可通过下式计算。

其中g4t,SU分别表示原始图像和加密后图像的像素值。理想的情况是灰度变化平均值等于K/2 (K为灰度图像的灰度级数)o对于灰度级为256的Lena图像，六态方案加密后图像(图3(d))的灰度变化平均值为78.159。BB84方案加密后图像(图3(b))灰度变化平均值为75.268．Logistic混沌加密后图像(图3(c))灰度变化平均值为77.235，相较于BB84方案和Logistic方案，基于六态密钥分配的图像加密方法的灰度变化平均值更接近理想情况，表明采用六态方案加密后安全性更高。

3、密钥敏感性分析

保持其它参数不变。Alice产生2个不同的二进制随机序列．Bob和Alice所选用的随机测量基序列也不同，加密后的图像亦不同。为分析加密方案对初始密钥的敏感程度，引入密文变化率Ct。

设定不同密钥对同一幅图像加密得到的加密图像为Cl，Cz，如果cI，C2对应的像素值q(i，j)=Cz(i，j)，那么D(i．j)=0，否则D(i，j)=l。

密文变化率如表3所示。由表3可看出，采用六态方案加密后产生的密文变化率大于BB84方案和文献中算法的密文变化率，表明六态方案对密钥敏感性更强。

4、抗噪声性能分析

为检测算法的抗噪声攻击性能，对加密后的图像分别加入椒盐噪声和高斯噪声，然后对其解密，结果如图5。其中图5(b)，(d)是分别对Lcna加密图像加入椒盐噪声和高斯噪声后的结果，图5(c)，(e)分别是对椒盐噪声和高斯噪声干扰后的密图进行解密后的图像。可以看出解密后的图像较好地复原出原图像信息，表明本文算法具有一定的抗噪攻击能力。

5、实时性分析

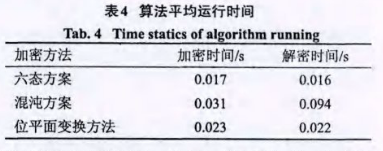
算法运行的时间是评价其性能的重要指标之一。在Intel (R) Pentium (R) Dual E2160@1.80 GHz，内存1.99 GB配置的计算机上，对256x256的Lena图像，利用基于六态方案的图像加密算法，对其进行加解密操作，获得算法的平均运行时间，并与基于混沌数列变换的加密算法和基于位平面变换的加密算法进行比较，结果见表40从表4可以看出，基于六态方案的图像加密算法加解密费时较少，实时性较高。