二叉树加密算法

二叉树加密算法是一种利用加密二叉树的树形对明文信息进行加密处理，同时还可以实现密钥的多方保存。

一、加密算法与构造二叉树

在运用基于二叉树的加密算法时，信息的管理者首先构造用于加密的二叉树，然后利用二叉树的树形对信息加密，将明文信息转化为密文信息。加密之后，信息的管理者将二叉树的前序遍历序列和中序遍历序列交给不同信息保存者，实现密钥的多方保存。

基于二叉树的加密算法就是利用二叉树来对二进制信息进行编码。我们定义用于加密的二叉树为加密二叉树Encryption_ Binary_ Tree=((To，Ti)l i=l，2，3，…，n，n>0），加密二叉树的任意一个结点用唯一的序号t来表示，加密二叉树是一棵树形不确定的任意二叉树，如图1所示D并且约定二叉树的左分支表示字符“O’’，右分支表示字符“1"。

首先，将需要加密的明文信息转化为二进制字符串，则加密过程是分解明文中的字符串，从根结点出发，按字符“0’’或“1"确定查找该结点的左孩子或右孩子，直至叶结点或者只有一个孩子的树结点，便得到了该子串相对应的结点序号。将结点序号按照明文的顺序排列在一起，即得到基于二叉树加密算法的密文，加密算法的密钥即是二叉树的前序（后序）和中序遍历序列。

假设需要加密的明文为：

00101101001001101000

则经过加密之后的密文为：

T3 T5 T6 T7 T7 T8 T5 T3

对密文的解密之后的明文为：

00101 101001001 101000

密文的形成是由二叉树的树形决定的，也就是说二叉树的树形对于算法的安全性有着极其重要的影响。下面我们来讨论构造二叉树的树形时应该注意的问题。

使用算法对明文进行加密前，首先构造一棵完全二叉树，然后随机对二叉树多次进行易位和剪枝两种处理，由此形成加密二叉树。

对结点TiI进行易位处理是指：交换二叉树中分别以t和Tj两个结点为根的子树的位置。

对结点tk点进行剪枝处理是指：将以tk为根的子树任意插入到一个孩子数小于2的结点之下，作为左孩子或右孩子。

虽然加密二叉树的构造是任意的、随机的，但是有些树形是不允许的。如只存在左枝或右枝的二叉树，这种二叉树在编码时，可以编码的信息有限，编码中包含许多连续的1，特征明显，容易被破解。完全二叉树也不允许，因为编码所用的二叉树是在完全二叉树的基础上变化而来的，破解者可能首先会尝试用完全二叉树来破解。

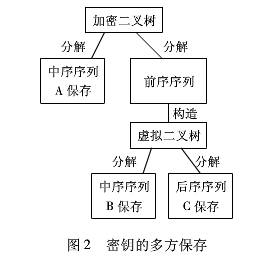
管理者在进行密钥的多方保存时，并不是只能将树形分给两个信息保存者，可以根据需要，将密钥分为任意多份。比如：需要将信息交给A、B、C三者保存，我们首先将加密二叉树的中序遍历序列交给A保存。我们利用前序遍历序列任意构造一棵二叉树，我们称这棵二叉树为虚拟二叉树，虚拟二叉树的树形与加密二叉树是不同的，但虚拟二叉树的前序遍历序列与加密二叉树的前序序列是相同的。将虚拟二叉树的中序序列和后序遍历序列分别交给B和C，如图2所示。这样便可以将密钥分为三份，需要分解为多份时，采用类似的方法利用虚拟二叉树的后序序列继续构造虚拟二叉树，提供虚拟二叉树的前序、中序序列继续分割。将密钥分为任意多份时，需要同时利用二叉树的前、中、后序序列，但只能利用二叉树的前序、中序序列构造虚拟二叉树，不能利用二叉树的中序序列构造虚拟二叉树，否则密钥无法继续分割。将信息保管者所保存的信息组合在一起构造密钥的过程，是密钥分解的逆过程。比如将A、B、C三者的二叉树遍历序列组合在一起，构造加密二叉树的树形时，先将B、C的序列组合构造虚拟二叉树气．并得到虚拟二叉树的前序序列，将虚拟二叉树的前序序列与A所保存的中序序列组合在一起，可以得到加密二叉树的树形，即密钥。

二、基于二叉树的解密算法

1、解密算法

对密文进行解密之前，首先需要将各个信息保存者所保存的二叉树遍历序列组合在一起，构成二叉树，然后对密文解密。

基于二叉树的解密算法是加密算法的逆过程。密文中的每一个字符对应二叉树的一个结点，在已知树形的情况下，从根结点出发到密文表示的相应结点的路径上，分支字符组成的字符串作为该密文字符所对应的明文段。将所有密文字符所对应的明文组合在一起，即是明文信息。加密算法的密钥就是二叉树的树形。

在实际应用中，明文的信息量是很大的，二叉树的结点数非常多，先构造二叉树，再进行解密的方法需要消耗大量的存储空间。解密的过程主要是在二叉树中搜索密文字符的过程，我们可以利用前序序列和中序序列所提供的信息，计算相应结点的左右孩子，在搜索序列的过程中，直接对密文解码。从二叉树的根结点出发，检查根结点或子树的根结点：如果该结点不是需要查找的密文字符，则搜索该结点的左子树，如果左子树中存在密文字符，则字符串增加一位O；以根结点的左孩子为根结点继续搜索，如果左子树中不存在，那么密文字符位于右子树当中，字符串增加一位1；以根结点的右孩子为根结点继续搜索，直到搜索到密文字符，此时就完成了对密文字符的解密工作。

我们用数组Preorder表示加密二叉树的先序遍历序列，数组Inorder表示加密二叉树的中序遍历序列，code表示密文对应的二进制字符串。具体算法如下：

Node_Code( Preorder[],Inorder[],SearchNode)

{

Preld=1；//指示根结点在先序序列中的位置。

Inld=1；//指示根结点在中序序列中的位置。

id =1；

n=l；

flag=0//标志位，指示根结点的左子树中是否

//存在需要查找的密文字符的标志位。

code[ n]；//记录密文所对应的明文信息。

while( Preorder[ Preld]! =SearchNode)

{/SearchNode为需要解密的密文字符；root=Preorder[Preld];While( Inorder[ Inid]!=root}

Gd++；//确定根结点的左子树的结点数目；

i(inorder[id]! =SearchNode) then flag=1;

//判断左子树中是否存在搜索的解密字符。

}

if flag=1

then{//搜索左子树

Preld++；

root = Preord[ Preld];

code[ n] =0

}

else{//搜索右子树

Preld = Preld + id;

root = Preord[Preld];

Inid =Inid +id -i

code[n] =1

}

id = 1;

flag =O;

n+ +;

}

}

用二叉树的先序序列和中序序列解密，在解密过程中，不再需要存储整个二叉树，只需要存储二叉树的前序序列和中序序列，大大降低了解密程序的空间复杂度。

2、加密算法的复杂度分析

我们首先分析解密算法的空间复杂度。加密二叉树的结点非常的多，假设为Ⅳ个，采用4个字节来记录结点信息，那么存储二叉树的先序和中序序列，总共需要个8Ⅳ字节的存储空间，这也就是解密算法所需要的存储空间。采用孩子表示法来存储一棵二叉树，一每个结点有三个域，其中的两个域，分别记录指向该结点左孩子和右孩子的指针，还有一个域用来记录结点的信息。在C语言中，一个指针需要占用4个字节的存储空间，那么存储一棵二叉树需要占用12N个字节的存储空间，加上本来就需要存储的先序和中序序列，那么不采用解密算法，总共需要20N个字节的空间。解密算法可以节约60%的存储空间。因此采用解密算法可以大大降低程序的空间复杂度。

再来分析解密算法的时间复杂度。解密的过程也就是从根节点出发，逐层向下搜索密文结点的过程。查找密文结点的次数，是由密文结点的所有祖先结点的左子树的结点数决定的。在加密二叉树与完全二叉树层数相同的情况下，完全二叉树的结点数多于加密二叉树，因此可以用完全二叉树来评估解密算法最坏情况下的时间复杂度。但是完全二叉树是不能用来作为加密二叉树的，它会降低算法的安全性。

假设完全二叉树一共有Ⅳ个结点，M层，由二叉树的知识可知M =lb(Ⅳ+1)，密文字符位于第K层。密文字符的祖先结点分别位于1，2，一”，K-1层，第i层祖先结点的左子树的层数为M-i;左子树也是完全二叉树，‘结点数为2Mi -1;'所以为了查找密文字符需要查找的次数为2M-K，当密文字符出现在二叉树底层最右边的结点时，算法的效率最低，需要查找-1次即N次，这相当于搜索了整个二叉树。因此解密算法最坏情况下的时间复杂度为O(Ⅳ)，但是正如上文所说的，完全二叉树不能作为加密二叉树，因此最坏的情况不会出现，解密时，搜索次数会大幅减少。

三、加密算法方案评价

基于二叉树的加密算法可以很好地实现对信息的加密，将二进制的明文信息对应于加密二叉树的结点，加密二叉树的树形不确定，无法对密文进行解密。为了进一步增强密码的安全性，我们提出对密钥实现多方保存，只有当所有的密钥的保存者都将自己的密钥提供出来时，才有可能对密文解密。解密算法利用二叉树遍历序列的性质，在不构造二叉树的情况下，直接利用二叉树的中序序列和前序序列对密文实现解密，降低了算法的空间复杂度。

加密二叉树的构造对密文的安全性有重要的影响，我们提出在完全二叉树的基础上随机修改，构造加密二叉树，但我们并没有给出具体的标准用来判断该二叉树是否可以用于加密操作，这是该算法需要进一步改进的方面。

admin普通用户

海报分享