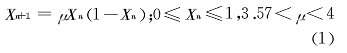为了降低图像存储的数据量,提高在现有通信信道容量下的信息传输效率,需要对图像进行数据压缩,因此,对压缩图像的加密显得尤为重要。为此我们提出了一种基于DCT量化系数重组的JPEG图像加密算法。
一、混沌系统
加密过程中需要用两类遍历矩阵对图像进行置乱加密,一类用来对明文图像进行以8×8图像块为单位的统一置乱;另一类用来对图像DCT变换量化后的系数重新组合后的8×8系数块内的系数进行置乱加密。利用混沌系统产生随即序列,然后对这该序列按大小进行排序,根据排序的序号可以产生所需要的遍历矩阵。
利用Logistic混沌映射生成第一类遍历矩阵Sa,用来对明文图像以8×8图像块为单位进行置乱,Losigstic函数如式(1):
利用Chen's系统构造第二类类遍历矩阵,Chen's系统描述如式(2):
式中,a、b、c为系统常参数,若它们取下列值:a=35,b=3,20 低频系数置乱;生成遍历矩阵Sb2用来对重组后的低频系数置乱。
二、加密算法
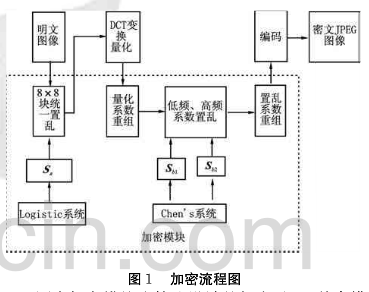
变换域中不同系数值代表着原始图像中不同频率的信息,每一个系数值的变化都会对整个图像产生影响,通过对变换域量化后的系数进行置乱,可以快速地改变图像的视觉效果,把图像变得杂乱无章、无法理解。置乱加密包括原始图像数据的基于8×8图像块的统一图像置乱加密和量化后系数的低频、高频系数分别置乱加密两个过程。具体的加密流程如图1所示,解密为它的逆过程。
图中加密模块为算法设计的加密过程,其余模块为JPEG压缩编码的标准过程。假设原始图像大小为M×N,其中,M表示图像的高度,N表示图像的宽度,由Logistic系统产生的随机序列{X(n)),生成一个大小为M/8×N/8的遍历矩阵Sa,再由Chen,s系统产生三个随机序列{x(t)}、{y(t)}和{z(t)},选取任意两个随机序列产生8×8大小的遍历矩阵Sbl、Sb2原始图像的DCT变换和编码是以8×8图像块为基本单位,因此对原始明文图像进行8×8块的统一置乱不会改变8×8图像块内部的像素之间的空间相关性,能够保持后续编码的结构不变性,不会增加加密后压缩图像的数据,而且可以使得图像在视觉上看起来杂乱无章.量化后的DCT系数低频部分一般非零值较多,而高频部分为非零值较少,按照zig-zag扫描进行游程编码,高频部分的零值系数对压缩率贡献较大.如果将两个8×8块DCT变换后的低频系数重新组合放在一起进行置乱,高频系数重新组合放在一起进行置乱,然后再将置乱后的高低频系数组合回8×8系数块,那么对游程编码的影响会较直接对8×8DCT量化后系数块置乱的影响小,对加密压缩后JPEG图像数据量改变不大。
1、量化系数重组
DCT变换和量化后的8×8系数块中左上角第一个系数称为零频分量,越往右下角频率越高,右下角最后一个系数称为最高频,用对角线将左上角和右下角进行平均划分,定义左上角的从左到右,从上到下的32个系数分量为图像的低频分量,右下角的32个系数分量为高频分量,如图2所示。
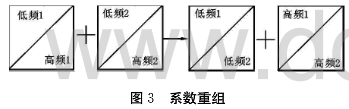
在进行系数重组时,相邻两个8×8系数块的低频分量组成一个新的8×8系数块,高频分量组成一个8×8系数块,如图3所示。
当8X8块内部的置乱加密结束后,再进行反向的系数块重组。
2、加密步骤
假设待加密原始图像为mXn,其中,图像高度为m,宽度为n,置乱加密算法如下:
(1)设定Logistic系统的参数:0≤Xn≤1,3.57<μ<4,为了保持序列的随机性,舍去序列开始部分,分别从序列的第ki (ki>400)个值开始,连续顺序取m/8×n/8个元素组成子序列sa;设定Chen's混沌系统的系统参数值:a=35,b=3,20400)、k3 (k3>400)个值开始,分别顺序选mXn/2、mXn/2个元素组成两个子序列S2、S3。
(2)将子序列Si按照从上到下,从左到右的顺序重排生成矩阵Mi;将子序列S2、S3分别分割成大小为64的子段S2j和S3j Q—o,每个子段按照从上到下,从左到右的顺序重排生成大小为8×8的矩阵MJ和M3j;
(3)用置乱矩阵固对原始图像mXn以8×8图像块为基本单位进行统一置乱,得到置乱后的图像。
(4)图像mXn进行DCT变换和量化,从图像左上角开始,按照从左到右,从上到下的顺序,首先对第0个和第1个8×8量化系数块进行系数块重组,组成低频系数块L和高频系数块日,利用置乱矩阵膨。和M30分别对其进行置乱加密,置乱后再将低频系数块L和高频系数块日进行反向系数重组。
(5)对第2j和2j+l量化系数块利用M2J和M3j分别进行步骤(4)的操作,直到所有系数块都加密完成得到加密图像mXn。
三、实验结果分析
在CPU为Intel双核3.3 GHz,内存为2.0 GHz的笔记本计算机上,利用Visual Studi0 2005 C++平台,取lena .bmp作为明文图像进行实验。Logistic系统参数取值为:Xo=0.901,μ=3.89,取随机序列的第一个值位置为ki一500;Chen's系统的参数取值为:a=35,b—3,c= 21.6,x0=0.15,y0=1.26,Z0=0.75,任取两个随机序列各取第一个值的位置k2=510,k3=520,系统时间参数t取值范围为t∈[0,150],采用步长为0.OOI的四阶五级Runge-Kutta算法求解混沌系统。
1、视觉效果分析
图4(a)为原始图像,图4(b)所示为加密后图像,图像大小为256×256,从加密后图像可以看到,加密后图像在视觉上已经无法看到原始图像的信息,达到了视觉上杂乱无章的目的。
2、安全性分析
(1)密钥空间
本文的密钥包括Xo,x0,y0,xo,y0,Z0,μ,k,k3,在window s平台32位机上,利用Visual studio2005 C++进行加密时,Xo,μ,c,xo,y0,Zo,ki,k2,k3这9个参数均取值为DWORD类型,取值空间大小均为232,那么密钥空间为232X9—2288,密钥长度远大于256比特,故加密系统能够有效抵御穷举攻击。
(2)密钥敏感性
解密时所用的Logistic混沌系统和Che‘s系统参数Xo,xo,yo,Z0,μ,任意一个与加密时的取值相差10 -12,而其他条件相同,都无法得到正确的解密图像。图5(a)所示为舶时得到的错误解密图像,正确输入密钥时解密得到图5(b)。可见算法具有很强的密钥敏感性。
3、对压缩影响分析
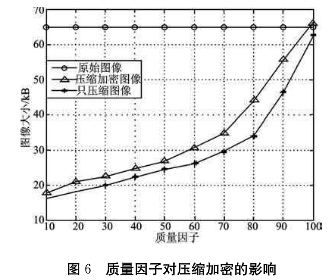
JPEG图像压缩主要是利用DCT变换量化后零值系数较多,而且zig-zag扫描时零游程较长的特点,非零值分布在低频系数区域,高频区域零值系数居多。将相邻两个DCT系数块的低频系数组合在一起置乱,而将高频系数组合在一起置乱,可以尽量较少的破坏零游程的结构,减少对图像压缩的影响,实验中压缩加密图像大小随质量因子的变化情况用matlab画图展示如图6所示(本例中使用原始图像大小为65.O kB)。
4、加密速度分析
使用置乱加密算法对DCT变化量化系数进行位置置乱,只是改变了图像的频率成分,在具体的加密计算中做了数据的位置变换,没有改变DCT量化系数值,较少使用乘除运算,因此加密速度比较快,可以满足实时性的要求,对不同大小的lenabmp图片进行压缩加密所使用的时间长度如表1所示。
小知识之DCT
离散余弦变换(DCT)是N.Ahmed等人在1974年提出的正交变换方法。它常被认为是对语音和图像信号进行变换的最佳方法。为了工程上实现的需要,国内外许多学者花费了很大精力去寻找或改进离散余弦变换的快速算法。由于近年来数字信号处理芯片(DSP)的发展,加上专用集成电路设计上的优势,这就牢固地确立离散余弦变换(DCT)在目前图像编码中的重要地位,成为H.261、JPEG、MPEG等国际上公用的编码标准的重要环节。