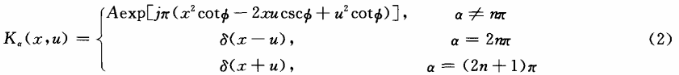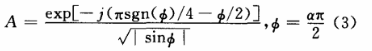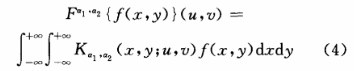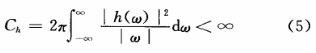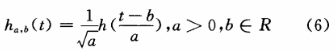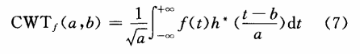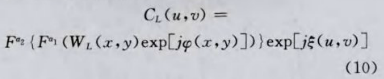为了提高图像加密的效率和实现分级加密,提出一种基于分数傅里叶变换和小波分解的彩色图像分级加密方案。通过对图像矩阵和颜色索引表分别进行加密来实现彩色图像的分级加密。
一、分数傅里叶变换
分数傅里叶变换是传统傅里叶变换在分数级次上的延伸。对输入函数f(x)的a阶次FrFT定义为:
其中Ka(x,u)为FrFT的核函数
二维的FrFT为:
其中a1和a2分别为傅里叶变换在x轴和y轴方向的阶次。由于FrFT的阶次可以作为密钥,将FrFT应用于图像加密可以进一步增强系统的安全性。
二、小波分解
小波变换是一种介于纯时域和纯频域分析之间的一种时频分析方法,可以表示为一个信号与某个核函数的修正形式乘积的积分运算,该核函数称为小波或小波基。用作小波基的函数必须是可允许的,即满足:
其中,h(w)为h(t)的傅里叶变换,h(t)称为一个基小波或小波母函数,式(5)称为允许条件。将h(t)进行伸缩和平移,设其尺度因子为a,平移因子为b。平移伸缩后的函数为:
hab(t)称为小波基函数,它们是由同一个母函数h(t)经过平移和伸缩得到的一组函数集合。信号f(t)的连续小波变换定义为:
在图像处理中利用二维离散小波变换可以将图像进行分解,得到图像的低频近似分量和水平细节分量、垂直细节分量以及对角细节分量。在得到各分量的情况下,可以利用小波逆变换重构图像。
三、加密算法
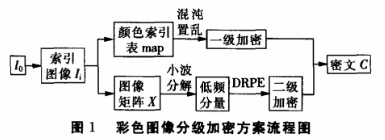
基于FrFT和小波分解的彩色图像分级加密算法流程如图1所示。
设待加密的原始彩色图像为RGB格式,记为I0,本加密方案的实现步骤如下:
(1)将输入的原始彩色图像I0转换为索引图像I0,索引图像可以表示为:
其中X为图像矩阵,map为颜色映射表。
(2)对颜色映射表map进行Logistic置乱,Logistic映射定义为:
其中,O≤μ≤4称为分叉参数,xn∈(0,1)为序列值。当3. 569 945 6≤μ≤4时,Logistic映射呈混沌态。Logistic产生的混沌序列具有很好的随机性,可以应用于序列的置乱。置乱过程如下:
(2a)按照Logistic混沌系统,选取合适的参数z.和弘进行迭代,如果置乱的序列大小为M×N,则n取M和N中较大的值,生成混沌序列S。
(2b)将生成的混沌序列S按照从小到大的顺序进行重新排列得到序列Q,找出序列Q中的元素在序列S中的位置,并生成位置序列L。
(2c)把颜色索引表的第i行整行移到第Li(i=l,2,…,M)行,L代表位置序列的第f个位置的值。移动完行后,再对列做类似的移动,即把第i列整列移到第Li(i=1,2,…,N)列。变换后的颜色索引表
达到了置乱的目的,与原图像矩阵结合得到一级加密图像。
(3)对图像矩阵X进行单层小波分解,单层小波分解后得到四个子分量,提取出低频分量WL作为后续加密的输入图像。
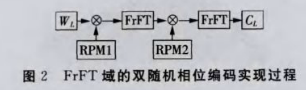
(4)对WL进行FrFT域的双随机相位编码(DRPE),得到二级加密图像。
其中,P表示阶次为a的FrFT。ψ(x,y)和ξ(u,v)为空间域和变换域的随机相位模板,相位值均匀分布在[O,2兀]。编码过程如图2所示,其中RPM1和RPM2分别代表随机相位模板。
(5)将加密的低频分量和水平细节分量、垂直细节分缝以及对角细节分屡进行小波逆变换合成图像矩阵的密文Xe。
(6)置乱的颜色索引表和加密的图像矩阵结合生成密文C。
本方案的主要密钥是:颜色索引表混沌置乱时的混沌序列初值XI和分叉参数μ,对图像矩阵进行双随机相位编码时使用的两个随机相位函数ψ(x,y)和ξ(u,v),两次FrFT的阶次Pi和P2,可见本方案有足够大的密钥空间保证图像加密的安全,可以抵御穷举法攻击。
解密过程为加密的逆过程。先对密文的图像矩阵进行小波逆变换,提取低频分量进行双随机相位的解码,然后与其他分量结合进行小波变换得到第一级解密图像,再对颜色索引表进行解密得到原始图像。只有当所有密钥均正确时,用户才能同时解密出图像矩阵和颜色索引表,获得正确的原索引图像。
本方案在加密过程中,由于引入了小波分解,只对图像矩阵经小波变换之后的低频分量进行加密,减小了计算复杂度,显著提高了加密速度。
本方案的特点是利用小波分解和分数傅里叶变换实现了彩色图像的分级加密。韩琦等提出的分级加密方案仅对图像矩阵进行了置乱,并没有改变图像矩阵的灰度值,安全性较低。在本文方案中,对图像矩阵进行了加密,提高了系统的安全性。在对图像矩阵经小波变换后的低频分量加密时采用了基于分数傅里叶变换的双随机相位编码,使方案既可以光学实现也可以计算机实现,加密方式更加灵活,如果使用光学系统实现加磷方案还可以进一步提高加密速度。
四、仿真结果
用一幅彩色图像Lena作为例子,在MatlabR2010a平台上进行仿真。图3(a)为待加密的真彩色图像Lena。图3(b)为索引图像的图像矩阵,图3(c)为第一级加密图像,图3(d)为图像小波分解之后各个分量的图像,图3(e)为选取的低频分量,图3(f)为加密图像,图3(g)为经过解密得到的一级解密图像,图3(h)为经过解密得到的二级解密图像。
为了测试密钥的敏感性,在对图像解密时,两次分数傅里叶变换的阶次误差分别为0. 05时的解密图像如图4(a)和(b)所示;随机相位函数错误时的解密图像如图4(c)和(d)所示;错误的混沌序列初值x1=0.5得到的解密图像如图5(a)所示,错误分叉参数μ=2.5时的解密图像如图5(b)所示。从解密图像中可以看出,此方案密钥空间大,密钥敏感性高,具有较高的安全性。
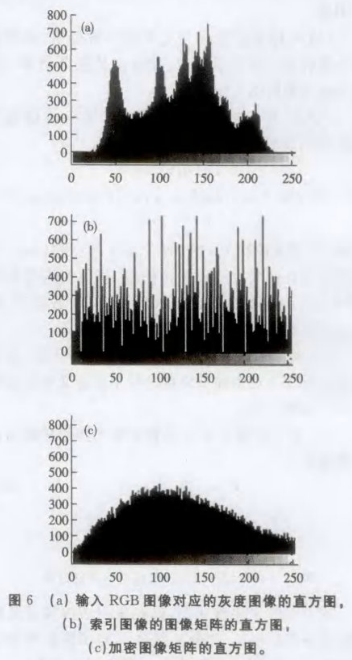
图像加密的目的就是使加密图像的直方图特征难以提取以保证图像的安全。图6显示了加密前后图像的直方图分布,图6 (a)为输入原始图像的直方图。显然,原始图像的直方图特征较为明显,安全性较低,不利于网络传输。通过分数傅里叶变换加密图像矩阵获得的第二级加密图的直方图如图6(c)所示,直方图改变很大,攻击者很难从统计特性中获得有用的信息。
小知识之小波分解
[c,l] = wavedec(s,3,'db1');
l是length的意思,记录的是由高到低各级的长度。
s代表进行分解的变量;
3代表分解层数
对1张图象进行小波分解,可以在MATLAB中实现。在COMMAND WINDOWS窗口中直接输入wavedemo进入说明,wavemenu进使用程序,也可以直接编程。程序在wavedemo里面自带。