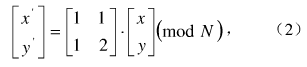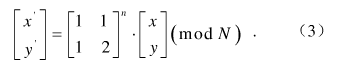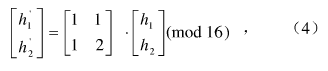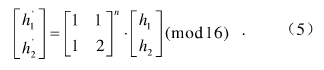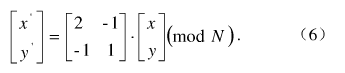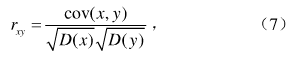为提升图像的置乱效果和置乱性能,提出了一种基于Arnold变换的双置乱图像加密算法。
一、Arnold变换
1、Arnold像素位置变换
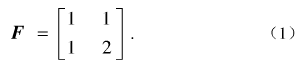
Arnold变换矩阵为:
二维Arnold位置变换表达式为:
式中,x,y,x’y’∈{1,2,…,N-1},N为图像矩阵阶数,x,y)为原始图像像素位置,x’,y’)为置乱后图像像素位置,在数字图像中,Arnold变换是将原来点(x,y)处像素值移动到变换之后的(x’,y’)点位置,通过变换图像会由清晰变模糊,当遍历了原始图像的所有点后,便产生了一幅相对原始图像混乱的新图。
对图像进行一次Arnold变换,相当于对该图进行一次置乱,通常这个变换过程需要反复进行多次才能达到满意效果,则对图像做n次Arnold位置变换的表达式为:
利用Arnold变换对原始图像置乱,使其变成像白噪声一样的毫无意义图像,实现了图像信息的隐藏,置乱次数可以做为密钥,从而增强了系统的保密性与安全性。
2、Arnold像素值变换
用办表示任意像素值十六进制形式,对其进行一次变换的表达式为:
式中,h=(h1,h2,)H,h’=(hi’,h2’)H是像素值h置乱后得至0的值,hl,h2,hi’,h2’∈(1,2,…,n)。
同样,为了达到满意的置乱效果,也需要迭代多次Arnold像素值变换,则对像素值h进行n次变换的表达式为:
3、Arnold逆变换
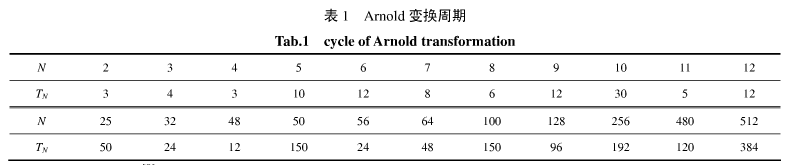
通常,求解Arnold反变换是通过计算其周期,表1给出了不同阶数N下数字图像的Arnold变换周期TN。
现有研究表明:若对一幅进行过n次Arnold变换的Ⅳ×Ⅳ数字图像(n>1)进行恢复,需要对其继续进行(TN-n mod TN)次Arnold变换即可得到原图像,这种恢复图像的方法要先检测图像大小和置乱周期,在处理较大图像时会花费较长时间,而在实际中应尽量减少其时间和空间复杂度。给出并证明了一种改进的Arnold反变换,无须计算图像周期,在置乱状态下迭代相J司步数即可恢复原图,节省了开销,称其为Arnold逆变换,即:
式(2)与式(6)有相同的周期.当一幅原图经过n步Amold变换得到置乱图像时,可以对置乱图像进行n步Arnold逆变换后恢复出原图,从而不必计算图像大小和变换周期,在本文算法中对密文图像解密时采用的就是Arnold逆变换。
二、双置乱加密算法
1、图像分块算法
图像置乱是为了降低图像邻域像素相关性,使图像的像素由最大确定性变为不确定性。为达到理想的置乱效果,可以采用的图像均匀分块算法,对于一幅原始图像,假设将其分成nxn个图像块,每块中有mxm个像素点,则置乱后的图像应分成mxm个图像块,其中每块中含有nxn个像素点,并且将原始图像每个图像块的mxm个像素点均匀分到置乱后图像的mxm个图像块中,保证每块图像中各含一个像素点,实现均匀置乱。
2、加密解密过程
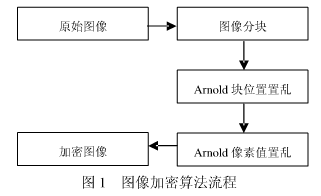
Arnold双置乱图像加密过程见图1。
先采用均匀分块算法对原始图像进行分块操作,然后分别对置乱后的每个图像块按式(3)做Arnold位置置乱,最后再按式(5)对合并后的图像做像素值置乱,从而得到杂乱无章的加密图像。
图像解密过程是图像加密的逆过程,首先,利用已知密钥(变换次数)对加密图像做Arnold逆变换,对图像像素值置乱进行恢复,然后执行图像分块算法,最后对图像块做Arnold逆变换恢复图像像素位置,从而还原出原始图像。
三、加密算法性能分析
下面通过实验对本文算法的性能进行验证。
1、加密效果
从图2可以看出,传统Amold置乱算法是对图像整体进行位置置乱,需要置乱多次才能达到理想的加密效果(见图2(b)),而且当迭代到一定步数时会恢复原图,加密系统安全性较低;而采用本文的双置乱加密算法时只要在较少的置乱次数下就能够达到理想的加密效果,而且采用双密钥决定置乱次数也提高了加密系统的安全性。
2、邻域像素相关性
通常一幅图像的相邻像素之间具有很大相关性,统计攻击方法常利用该性质来分析图像加密算法。置乱后图像相关性越小说明图像加密效果越好,用相关系数来衡量加密算法对邻域像素相关性的破坏能力。本文对图2 (a)图像进行测试,分别随机选取1 000对相邻像素点(水平方向、垂直方向、对角方向),记为(xi,Yi) (i=l,2,3,…,N),利用式(7)计算相关系数,
式中:
和D(x)分别是xi的离散化均值和方差。
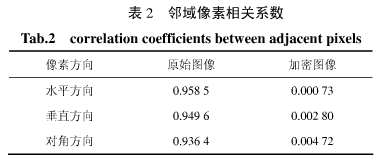
图像加密前后邻域像素相关系数见表2。从表2可以看出,原始图像在水平、垂直和对角3个方向的像素相关性都非常高,而加密图像的相关性非常小(接近于0),故本文算法具有很强的抗统计分析攻击能力。
3、抗剪切性能
利用Adobe photoshop软件对已加密图像图2(d)进行裁剪,裁剪方案见图3(a),然后对裁剪后的加密图像进行恢复,恢复效果见图3 (b)。
由实验结果得知,对裁剪图像进行恢复后会存在一定程度失真,但还是会很容易辨认出图像所表达的信息.本文算法由于采用了均匀分块和图像块置乱思想,使得每块图像中的像素都能够均匀分布到其他各个图像块中,削弱了图像邻域像素相关性,从而能够有效地抵抗局部随机裁剪攻击。
小知识之Arnold变换
Arnold变换是一种常用的图像置乱技术,Arnold变换的定义如下:
对任意N*N矩阵(所有元素都相同的矩阵除外),设i,j为矩阵元素原始下标,经过Arnold变换后新下标为i',j',且满足下式:
i'=(i+j)mod N
j'=(i+2j)mod N
i,j:0,1,.........N-1
Arnold变换具有周期性,即经过若干次变换后,矩阵回到最初状态,且周期T与N的大小有关。理论基础没找到,但可以用程序来进行计算,可以设i,j从一个点出发,不断使用以上变换,再次回到这个起点时,经历的变换次数就是周期。