三维arnold变换图像加密算法
目前我们常用的图像置乱加密基本上都是基于二维变换的,要达到较好的置乱效果,往往需要进行多次操作,置乱效率不高。为达到较高的置乱效率,提出了一种新的三维Arnold变换和混沌序列相结合的图像加密算法。
一、三维Arnold变换
假设某一图像像素的坐标位置为xy∈{1,2,…,N},则二维Arnold变换可以定义为:
其中x’,y’表示经过Amold变换后的图像像素的坐标位置,此变换称为二维Arnold变换。可将二维Arnold变换扩展成三维Arnold变换,其形式如下:
三维Arnold逆变换为:
其中矩阵c是矩阵A的逆矩阵,
则对应的矩阵A的逆矩阵为:
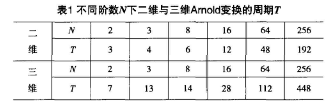
三维Arnold变换与二维Arnold变换一样,也具有周期性,即经过若干次变换后,图像又变换为原始图像。表1列出了不同阶数Ⅳ下二维与三维Arnold变换的周期丁。从表中可以看出,相同阶数N的情况下,三维Arnold变换的周期总体上要大于二维Arnold变换的周期。
二、Logistic混沌映射
Logistic映射是由数学生态学家May于1976年提出的,其表达式为:
当3.56994< &L≤4时,Logistic映射将处于混沌状态。 三、图像加解密算法 本文利用三维Arnold变换和Logistic混沌序列分别对图像进行置乱和异或操作,从而得到加密图像,解密与加密过程相反口具体的加解密步骤如下: (1)选取一幅mxn的灰度图像作为待加密图像,获得其二维矩阵数据P,并对图像进行如下转换:找到一数值N,使得mXn=N3或mXn≈N3。若mXn的值不等于任何数值的三次方,则取最小N值,使得N3>mxn,然后按矩阵的行(列)顺序读取尸的元素并依次放至三维零矩阵B中,矩阵B的大小为N×N×N;
(2)将处理后的三维矩阵B的像素位置坐标(x,y,z)代人方程(2)中,其中x,y,z∈(1,2,…,N),做若干次三维Arnold变换得到置乱后的三维图像信息矩阵Pl;
(3)选取合适的μ,x0代人方程(7)中,迭代次得到一组混沌序列xi,其中k>N3,i=l,2,…,k;
(4)从步骤(3)中获得的混沌序列yj中随机从某一值开始依次取像素组成混沌序列j=l,2,…N3并对Yj作相应处理,具体处理如式(8)所示:
(5)将步骤(4)中得到的混沌序列Yi的元素顺次放入三维矩阵D中,D的大小为NxNxN,然后将D与步骤(3)中得到的置乱后的图像信息矩阵P1进行逐位异或运算操作,得到加密后的图像信息矩阵P2;
(6)将步骤(5)中得到的加密图像矩阵P2中的元素依次放入二维零矩阵P3中,P3的大小为mxnl,其中mXn1≈N3。若没有这样的整数nl,使得mXn1=N3,则取最小的值nl,使得mXn1>N3,而二维矩阵P3中仍
有mXn1=N3个零元素,本算法中取数值为0~255的整数混沌序列进行填充,再将信息矩阵按照图像标准格式保存,得到最终的加密图像;
解密算法就是加密算法的逆运算。
四、仿真分析
1、实验结果
为验证本算法,本文选取p=3.767835609687648,x0-0.565786987640228作为Logistic映射的加密密钥,对图像进行三维Amold变换的次数为4次,按照加密步骤对图1所示图像“stone’’进行加密,图像大小为492 x 738,重构后的三维图像矩阵大小为72×72 x72,加密后的图像大小为492×7590其中图l为原始图像,图2为加密图像,图3为解密图像。
由图1和图3中可以看出解密图像与原始图像一致,说明解密无误,而通过图2则说明了最终加密后的图像很好地隐藏了原始图像中的数据,说明加密成功。
2、置乱度分析
图像的置乱程度可从主观和客观两个方面进行分析。主观方面,一般认为置乱程度比较好的图像是通过人眼不能观察到原图像所包含的信息,下面运用二维Arnold变换和本算法中的三维Arnold变换对图像“grass”进行不同次数的置乱并进行对比,图像大小为216×216,“grass”原始图像如图4所示,实验结果如图5所示。
由图5可以看出,二维Arnold变换要想达到较好的置乱效果,需进行多次反复置乱操作,而本算法中运用的三维Arnold变换经过一次置乱就达到了较好的置乱效果,置乱效率较高。
3、统计直方图
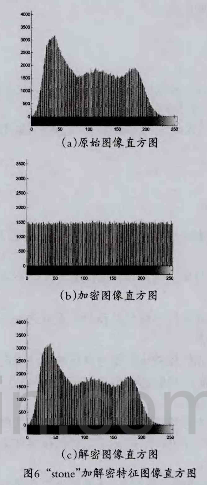
图6(a)显示的是图l所示原始图像“stone”对应的直方图,图6(b)所示为图2所示最终加密图像的直方图,图6(c)所示为图3所示解密图像的直方图,由图6(b)可以看出,加密后的图像直方图分布均匀,将原始图像信息特征完全隐藏起来,说明加密性能良好,而原始图像和解密图像的直方图完全一致,说明解密成功。
4、像素相关性分析
经实验测试,图1所示原始图像“stone”和其加密图像(图2)的各方向相邻像素间的相关系数如表2所示,由表2可知,加密后的图像相邻像素的相关性大大降低,可有效抵抗攻击者的统计分析。
小知识之Arnold变换
Arnold变换是一种常用的图像置乱技术,Arnold变换的定义如下:
对任意N*N矩阵(所有元素都相同的矩阵除外),设i,j为矩阵元素原始下标,经过Arnold变换后新下标为i',j',且满足下式:
i'=(i+j)mod N
j'=(i+2j)mod N
i,j:0,1,.........N-1
Arnold变换具有周期性,即经过若干次变换后,矩阵回到最初状态,且周期T与N的大小有关。理论基础没找到,但可以用程序来进行计算,可以设i,j从一个点出发,不断使用以上变换,再次回到这个起点时,经历的变换次数就是周期。