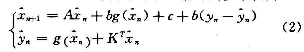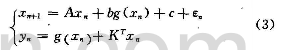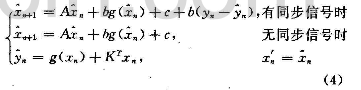利用混沌同步进行加密是当前信息安全的一个热门研究领域,它不但具有良好的实时性,而且可以有效地避免混沌密钥序列的周期性,其主要难题是如何传输混沌同步信号。
数字音频加密
1、数字音频加密方案
整个加密系统的原理如图l所示。加密时,对混沌系统引入随机微扰。,破坏由有限字长所造成的数值迭代的周期性,从而使混沌系统的状态变量,具有更高的随机性。首先,分析音频序列{s),找出冗余信息的位置。然后,对于冗余的位置,将同步信号y.以加密算法R进行加密,得到加密的同步信号{kn);对于非冗余的音频信息,用z一以算法K生成密钥序列{kn),并利用该序列以加密算法C对这些音频加密,得到加密的音频。直接合并即为最终的加密音频。解密过程刚好相反。
从上述的加密和解密过程可以看出,该方案密钥除了可来自混沌系统的参数之外,还可以来自加密过程K,C和R,所以本方法拥有广阔的密钥空间。另外,C和R还可以采用现有的数字加密算法。每一个环节在解密时都必须正确无误,所以本方案具有很强的抗破解能力。
本加密方案中,有三个关键问题需要解决:
(l)采用何种混沌同步方法,使在传输尽可能少的同步信号的情况下,得到.更小误差范围内的近似同步;
(2)如何确定冗余信息的位置,从而在保证能够实现混沌近似同步的情况下,尽可能缩小恢复音频与原始音频之间的差别;
(3)如何从(S:)中区分出同步信号来。:这三个问题直接决定了通信的质量。
下面以二维超混沌映射为例来进行详细说明。
2、一类二维超混沌映射的近似同步
现在,以一类二维超混沌映射的某组参数为例来进行讨论。该类超混沌系统方程为:
其中yn是标量输出,g:R2一R是非线型函数,A∈R2X2,6,c,K∈R2为参数。表1为一些超混沌参数和系统的Lyapunov指数。
根据Dead - Beat同步方法,它的同步系统为:
则其同步误差显然,若r6AbA2b ”一 A-lb]满秩,A一bKT的所有特征值可以通过K任意配置。即存在一个K使A -bKr的所有特征值都为0,经砚步迭代,e(k)=O,达到完全同步。
在本加密方案中,对式(1)引入随机微扰:
同步系统为:
如果£充分小,有同步信号时,经Z.步达到误差接近的近似同步;没有同步信号时,经l2步这个误差会慢慢放大至恢复密钥序列所容许的误差范围的边界附近。对于这类二维超混沌系统而言,约为2或3,而Z:远大于Z。这样一来,只要每间隔不超过如步,发送3步混沌同步信号就能准确恢复密钥序列实现解密。
3、音频样点是否冗余的自适应判别方法
若相邻三样点sn,sn+l,sn+2冗余,则取其前后各2个样点组成四个采样点,用三次多项式插值恢复出的三个样点信息为:
定义误差距离为:
判别相邻的三个样点是否为可替换成同步信号的冗余音频,其自适应算法如下;
(1)信号开头的三个样点可直接替换成同步信号
(2)计算dr+12/2+3~d卧f:+3,找到其最小值di。为冗余音频样点,可替换成混沌同步信息。重复该步直到音频信号结束。
4、同步信号的自动判别算法
在解密时,首先要从接收到的加密信号S:中分离 出混沌同步信号,并进行混沌同步。其算法如下:
(l)令混沌同步标志T-O。
(2)若信号结束,算法完成。
(3)说明假设不成立,令n- n+l,返回(2),否则进入(4)。
(4)若T—O,令y—-2也为同步信号,代入式(4)迭代一步。
小知识之同步信号
同步信号是指在同一载体内同时发出的多个信号源,使接收者能收到更多或更好的信息。同步信号应包含行同步信号、场同步信号和色同步信号(彩色负载波)三种。