全同态加密算法

为确保云计算环境下用户数据的安全性，利用同态加密算法对数据和加密函敦的隐私保护功能，设计一种基于整数多项式环的全同态加密算法。该算法包括同态算法和重加密算法，前者针对明文数据进行加密，后者针对密文数据进行二次加密。

一、基于整数环的全同态加密算法

1、全同态加密算法发展现状及数据保护特点

全同态加密算法颠覆了传统意义下的加密模式（图1、图2），它是一种可以对密文进行操作但仍可以恢复明文的加密算法。算法设计的目的是：解决云环境下数据上传服务器端，Sever不可信，用户把私有数据加密上传服务器端。全同态加密算法最终实现：

这样用户可以把私有信息经过加密上传服务器端，享受云服务，但是服务器端并不能获得用户数据。因此全同态加密算法可针对用户的需求满足对加密信息和加密函数的保护，使得在整个传递过程当中始终保持加密状态。

加密信息的处理如图3所示，主要是对私有信息进行保护。Alice有私有的函数fA和私有的信息XA，Bob把私有信息yB用私有公钥pkB加密得到E(y)发送给Alice，Alice用自己的私有函数fA加密私有信息XA和E(yB)，由于同态性质，函数fA被隐藏，而Bob获得E(fA (XA，yB)）。Bob通过私有的私钥加密D(E(fA (XA，yB)））=fA (XA，yB)。

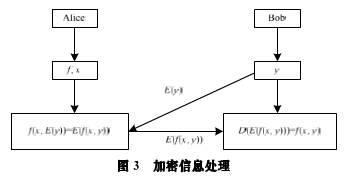
加密函数的处理如图4所示，主要是对私有的操作函数进行保护。Alice有私有的函数以，并用私有公钥pkA加密函数fA发送给Bob，Bob根据私有信息XB计算E(fA )(XB)，由于同态性质，因此隐藏了Bob的信息XB，得到E(fa(b))，并发送给Alice，Alice用私钥解密获得fA(XB)。

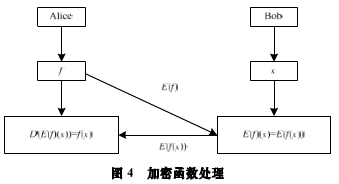
2、整数环全同态加密算法分析

由于理想格全同态加密算法复杂度高，且密文数据扩张不能得到解决，因此实用性不强。根据已有的理想格和整数全同态加密算法，设计基于Fp[x]的全同态加密算法。

同态算法具体如下：

KeyGen：对f(x)∈Fp[x]，选择随机的整数ai，ri∈Z，因此公钥pk=，对每个b，满足bi =aif(x)+ri，b最大。

Encryption：随机选择一个整数子集S∈{1，2，…，，z}，m∈{O，1}，随机选择r∈(_22p，22p)，密文ci= [m+2r+2∑i∈sbi]modbo。

Decryption：m=[cmodx]mod2

同态性性质：

(l)加法：给定公钥pk，密文Cl、C2，则：

(2)乘法：给定公钥pk，密文cl、C2，则：

其中，Lxl表示x向下取整；rxn表示x向上取整。

加解密正确性分析：

(l)设需要加密的明文信息为m=l或m=o，选择的函数为Z (x)，选择n+l个q和n+l个l，S={1，2，…，n）。

(2)计算n+l个bi，使得bo次数最高。

(3)加密明文信息朋，得到c=[m+2r+ 2∑i∈Sb]modbo。

(4)不妨设f取得s集合中的前k个bi。

(5)密文c可以写成：

(6)c是满足多项式形式的数据，即c=g(x)x+n。

重加密算法Evaluate具体如下：

Keygen：按照上述算法选择公钥pk和私钥sk，选择k，其中，尼是满足计算安全的大素数；p是同态算法中的Fp [x]，定义xp=[2k/p-1/2]，汉明重量为θ的多项式g(x)=∑gixi，θ为2个a的最大距离，Ci∈z n[o，2k+l)，使得∑iESCi=m(mod2k+J)，Yi=ci/2k，因此可以得出∑i#sci=mod2k+1，新私钥sk'=< g1，92，…，gn>。

Encryption：

输入：密文c，新公钥pk'；

输出：新密文c’= [c. Yi]mod2 0

Decryption：

输入：新密文c’；

输出：

整个算法的设计思路是通过多项式的次数、模运算、交互运算以达到混乱明文的作用。在设计过程中主要是考虑把问题的复杂性归结到离散子集求和问题，因此，选择多项式是该算法的关键环节，多项式的选择可以根据加密方对安全的要求程度决定，例如安全程度低可以选择f(x)=x+1，如果安全程度高可以通过提升f (x)的次数来加强。同态算法的设计还是延续了理想格方法和整数方法的特点，使得循环操作环节简单，便于实际应用。

性质基于整数环Fp[x]的全同态加密算法计算量是O(Y15)。

证明：在Evaluate运算中，需要确定xp、ci、Yi、Encryption和Decryption 5个部分，输入的pk={bl，b2，…，bn）有n个，需要计算量为n；c=m+2r+∑iES bi ]mod bo，计算量为n；加密运算和解密运算需要计算量为n；每个重加密运算都需要挖次操作，所以，计算量大约为：在实际应用中，存在匿名同态协议和一种半匿名，即相邻结点间不是匿名的，非相邻结点间是匿名的。另外还存在一个乐观可信第三方(optimistic trusted third party)，用于解决当出现非法访问时去找到那个非法访问者，该TTP只有在出现问题时才存在，所以不会影响效率。同态加密技术的快速发展，在云数据检索、投票、垃圾邮件过滤、信号分析领域都有着广泛的应用。在安全协议上，同态算法都是解决一些关键问题的有效方法和手段。

三、算法性能比较

全同态加密算法的主要优势是可以针对密文进行操作，仍然可以回复明文，因此，满足用户对云服务的基本要求。本文算法与2种全同态加密算法进行比较（表1）：

(1)理想格全同态加密算法：需要进行矩阵运算和向量模运算（向量的加法和乘法），每加密一个比特都需要进行矩阵和向量运算（表示为连续性不好），公钥扩展O(n7)，每个Evaluate中计算门的计算量为O(n6)。

(2)整数全同态加密算法：需要进行整数模运算，连续性好，Evaluate算法中输入超过本身算法要求，就不会实现全同态的性质，存在攻击危险。每个Evaluate中计算门的计算量为O(y13)。

(3)整数环全同态加密算法：主要进行多项式运算，加密过程中不需要重新选择多项式（连续性好），Evaluate中计算门的计算量为O(Y5)，根据实际安全的级别进行筛选。

在算法的设计环节，虽然没有保证严格雪崩效应，但是把算法的安全性依靠在离散子集求和这个难解问题，因此安全性没有受到影响，而且有更好的实现价值。今后需要对降低基于整数多项式环的全同态加密算法的时空开支以及明密文数据的扩散问题进行研究。

admin普通用户

海报分享