为了更好地将传统的Feistel加密结构应用在图像加密中,将加密与混沌系统结合起来,在混沌图像加密的基础上,提出了一种基于超混沌序列和Feistel结构的图像加密算法。
一、加密算法原理
1、超混沌系统
超混沌系统一般具有两个或以上正的Lyapunov指数,由于其具有比普通混沌系统更大的可用密钥空间,可以提高系统的抗破译能力。也有资料给出的图像加密算法用到了Kawakami和Hyperhenon映射两个超混沌系统。
Kawakami混沌映射的定义如下:
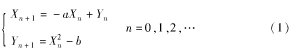
其中,a=0.1,b=1.60时,系统处于超混沌状态,Kawakami混沌映射本身是一种超混沌序列。此处取X0∈(O,l)。
Hyperhenon混沌映射的定义如下:
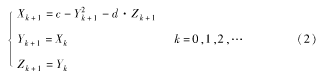
其中,c=1.76,d=0.1时,系统处于超混沌状态,Hyperhenon映射本身就是一种超混沌序列。此处取X0∈(O,l)。
本文设计的图像加密算法还将用到Logistic混沌映射,其定义如下:
![]()
其中当3.5699456--≤μ≤4,(O<xn<1)时,系统进入稳定的混沌状态。
2、图像预处理算法
为了增强加密算法的安全性,首先对待加密的图像进行预处理。本文以Kawakami超混沌映射为例,首先介绍预处理过程。设原始图像形的大小为MxN,相应的预处理算法描述如下:
a)给定Kawakami映射的初始值xo、Yo,利用式(1)通过迭代计算产生两个混沌值xl和Y1,将第x1放人数组a,Y1放人数组b,将x1、Yi再代人式(1)迭代产生X2和Yz,X2放人数组a,y2放人数组b。以此类推,直到不满足<MxN则停止。
b)分别对数组口和6中每个混沌值进行变换,取每个混沌值小数点后的第3—5位组成一个新的三位整数L,然后L对256做取模运算,将数组口中每个新得到的整数依次放人大小为MxN的矩阵A,同样将数组b中新得到的整数放人大小为MxN的矩阵B。
c)将两个矩阵A与B其中的每个值转换为二进制序列,并放回A和B矩阵。
d)将原始图像W的像素值转换为二进制序列,与步骤c)所得到的序列矩阵A与B做异或运算。
e)将异或后的结果转换为十进制放入图像矩阵W中,完成图像的预处理,得到预处理加密图像w1。
图像的预处理算法虽然只是对原始图像做简单的异或运算,但由于是基于超混沌序列的,为整个算法的安全性提供了一定的安全保证。图l给出了预处理的基本流程。
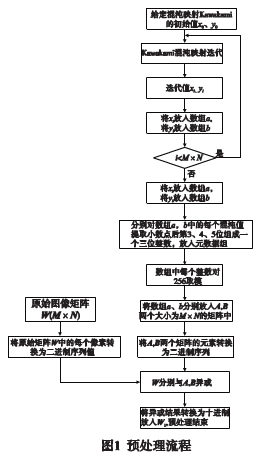
3、图像加密算法
在预处理的基础上,利用Logi8tic混沌序列生成Hyperhenon超混沌的初始值,再由Hyperhenon超混沌序列产生S盒,使用Feistel结构对图像进行加密。具体的加密过程如下:
a)将经过预处理后的图像矩阵W的每一行分为左右两部分,分别记为Li0和Ri0。
b)给定一个初始值zo,利用Logistic映射,即式(2)迭代生成48个序列值,以第j,j+16,j+32个序列值作为第j轮的子密钥,记为Kj。代入Hyperhenon混沌映射,通过迭代计算每轮生成三个混沌序列值x、y、z,通过16轮迭代计算,生成的混沌序列分别组成X、y、Z三个16×(N/2)的矩阵。
c)利用X、y、Z构造S盒,对X、y、Z每个矩阵中的每一行作升序排列,得到矩阵XL、K、zl,然后将X、y、Z在Xl、yI、Zl中的位置作为置换矩阵p、q、r。此时p、q、r矩阵的每一行就是Feistel结构中第i轮的S盒,每一轮共有三个。
d)取预处理图像的第一行Lio和Rio,将Rio经过三个S盒的置换,然后与Lio进行异或,得到的结果作为下一轮循环的Ru,而下一轮循环的Lii则等于Rio。
e)利用p、q、r三个S盒中的2—l6行重复d)。
f)合并得到的结果Ll16和Rl16放入图像矩阵中。
g)对预处理图像的每一行重复d)e),最终得到的图像就是加密后的图像W2。
加密算法的基本流程如图2所示。

本文中的加密算法是基于超混沌序列的Feistel结构加密,使得系统可以较好地抵御差分攻击。
解密过程与加密过程基本一致,只需要将子密钥逆序输入即可解密图像。
小知识之Feistel 结构
在密码学研究中,Feistel 密码结构是用于分组密码中的一种对称结构。以它的发明者 Horst Feistel 为名,而Horst Feistel 本人是一位物理学家兼密码学家,在他为 IBM 工作的时候,为Feistel 密码结构的研究奠定了基础。很多密码标准都采用了Feistel 结构,其中包括DES。Feistel 的优点在于:由于它是对称的密码结构,所以对信息的加密和解密的过程就极为相似,甚至完全一样。这就使得在实施的过程中,对编码量和线路传输的要求就减少了几乎一半。







