针对DES对称加密算法中密钥安全性保密困难且不易管理、RSA非对加密算法加密速度慢不易实现的缺点,我们在研究信息明文与随机产生的加密密钥之间的异或运算进行信息明文加密、同时将信息明文的加密密钥按RSA算法进行加密管理以安全的传输到接收方,基于此,提出了一种基于异或运算的混合加密算法。
一、DES对称加密算法
DES对称加密算法是由IBM公司在70年代初为硬件应用而设计的,之后由美国政府作为一个官方标准定义和支持的加密法。DES加密算法自公布之日起,人们就对它进行了深入的研究,它是世界上最为著名的、使用最为广泛的加密算法之一,一直应用于银行业和金融界。
DES算法加密信息的基本工作原理是:
(l)通信开始之前,收发双方共同协商约定一致的密钥Key用于信息明文的加密。
(2)通信开始后,发送方首先用密钥Key对信息明文进行16轮迭代置换运算形成加密密文,通过传输系统发送到接收方;接收方收到来自发送方发送过来的密文信息,用密钥Key对密文信息采用同样的算法进行反方向的16轮迭代置换运算还原得到信息明文!
由此可以看出,DES对称加密算法由于收发双方采用相同的密钥进行信息的加密解密,因此DES对称加密算法的优点是易于实现、速度快;但是,DES对称加密由于算法是完全公开的,它的安全性完全依赖于密钥的保安性强度,在多用户之间进行通信加密时,每一对用户需要使用一个密钥,N个用户就需要使用Ⅳ(N-1)/2个不同的密钥,这样才能保证收发双方收发密文时第三者无法了解其所使用的密钥和密文内容,当N很大时,记住如此多的密钥是不可能的,而保留起来又会引起密钥泄漏的可能性增加,另外,如何安全地将加密解密所使用的密钥传送给对方,也是一个必须考虑的问题。因此,DES对称加密算法的缺点是安全性低、密钥管理不方便。
二、RSA非对称加密算法
RSA非对称加密算法又称公钥密钥算法,采用RSA算法加密的通信系统中,收发双方都拥有一对不同的密钥,其中一个在通信系统中公开,发送方通过获取此密钥来加密信息明文,这个密钥称为公钥;另一个密钥接收方用于解密密文信息,称为私钥,且私钥和公钥是不同的、解密用的私钥不能根据加密用的公钥计算出来。公钥和私钥成对出现,而且两个密钥之间存在数学关系。这种数学关系指的是RSA算法的理论基础,初等数论中的质数分解因子。众所周知,将两个质数相乘,乘积是很容易算出的。但反过来要将这个乘积值再分解成原来的两个质数却相当困难了,因为即使是速度最快的计算机,要将一个大的乘积分解还原为得出此积的两个质数也要很长的时间。只要乘积的位数足够长,要想将乘积分解还原几乎不可能,据数学家推算,用可预测的未来计算能力分解两个250位长的质数的乘积要用几百万年。因此,RSA非对称加密算法的优点是安全性高,用户不必记忆大量的提前商定好的密钥,密钥的管理简单方便;缺点是加密速度慢,在选择密文攻击面前很脆弱。
RSA算法步骤如下:
(1)选取两个足够大素数m和n,并计算其乘积s =m*n。
(2)随机选取加密密钥e,使得e与(m-l),(n-1)互素。
(3)求解密钥d,以满足ed≡lmod(m-1).(n-1),从而求得解密密钥:
![]()
(4)公开e和s,将d保密,丢弃m和n。
(5)加密明文信息p时,首先将它分成比s小的数据组。例如,m和n为100位的素数,那么s将有200位,每个信息分组应小于200位长(如果需要加密固定的消息分组,那么可以在它的左边填充一些0并确保该数比s小)。
现假设按上述分组方法将加密信息p分成了k组P1,P2,…,pk,而加密后的密文C也将由相同长度的分组Ci(i=1-k)组成,则加密公式简化成:
![]()
(6)解密信息时,取每一个加密后的分组Ci(i=l一k)并计算。
![]()
三、基于异或运算的混合加密算法
1、加密算法思路
(1)异或运算:对于任意一个数A,随机的任意选择另一个数B,则A与B具有如下异或运算性质。
如果把A理解为信息明文,B理解为加密密钥,C理解为信息密文,则公式正好符合对称加密算法的定义。
![]()
(2)对称加密算法中,算法的安全性强度完全依赖于密钥的安全性、且密钥的管理也极不方便,RSA算法采用数学界有名的质数分解因子理论来加密信息明文,如果把对称加密算法中的密钥当成RSA算法中的信息明文进行加密,其安全陛将达到RSA算法同样的强度、密钥的管理也十分方便,且运用RSA算法对密钥这一小部分信息进行加密比对整个信息明文中的大量信息加密处理起来速度快得多。
基于以上两点思路,提出一种基于异或运算的混合加密算法(Hybrid Encryption AlgorithmBased On XOR,HEA - XOR),该算法的基本原理是:在任何通信系统中,首先,收发双方准备好一对密钥,一个作为公钥公开在通信系统中,发送方通过获取此公钥用于加密明文加密的密钥;另一个作为私钥,接收方保留用于解密明文加密密钥的密文。然后,在信息通信过程中,发送方随机产生一个数作为对信息加密的密钥,并用接收方公开的公钥对此产生的随机数密钥进行加密,最后再将信息加密之后的密文和密钥加密后的密文一起发送到接收方;接收方收到发送方发送过来的信息密文和密钥密文后,用自身保留的私钥对密钥密文进行解密,得出信息加密的密钥,再用得到的信息加密的密钥对信息密文进行解密,最后得出原始的明文信息。综上所述,运用HER - XOR算法对信息加密的思路是,基于二进制的异或运算,收发双方用相同的密钥对信息明文进行加密解密,基于RSA算法对密钥进行加密解密,以实现密钥的安全传输与管理。
2、加密算法描述
HER - XOR算法密码系统工作模式如图所示。
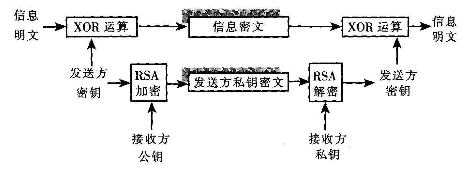
从图2可以看出,实现HER - XOR算法密码系统可按如下步骤进行。
(1)接收方根据RSA算法原理得到自己的公钥和私钥,并在整个密码系统中公开自己的公钥,并保留自己的私钥。
(2)发送方利用自己的密钥(发送密钥是随机产生的)对信息明文进行XOR运算(二进制异或运算)加密,再用获得的接收方公钥对自己的密钥进行RSA加密运算,最后将得到的信息密文和发送方私钥密文通过通信系统发送到接收方。
(3)接收方收到发送方发来的信息密文和发送方密钥密文后,首先运用自己保留的私钥,对发送方密钥密文进行RSA解密运算,得到发送方密钥,再用此发送方密钥对信息密文进行XOR运算解密,以还原初始信息明文。
小知识之异或
异或,英文为exclusive OR,或缩写成xor
异或(xor)是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”,计算机符号为“xor”。其运算法则为:
a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
异或也叫半加运算,其运算法则相当于不带进位的二进制加法:二进制下用1表示真,0表示假,则异或的运算法则为:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同为0,异为1),这些法则与加法是相同的,只是不带进位。





