21世纪是一个信息化的时代,人们之间的信息交流是越来越频繁,关于信息的安全和保密问题也就成了人们越来越关注的问题。因此,各种类型的图像加密技术也就应运而生。Fridrich最早在研究图像加密时将混沌理论应用在其中。从此以后,基于混沌的图像加密技术受到越来越多研究者的关注,它作为一种新的图像加密技术得到了飞速的发展。但是,在目前用得比较多的伪随机序列中普遍存在着周期有限长,可用的优码数量少,线性复杂度低,容易被破译等缺点。
然而,混沌具有天生的密码学特性,而且利用它产生的伪随机序列可以很好地克服上述的不足之处。同时,细胞神经网络(CNN)具有非常丰富和复杂的非线性动力学特性,利用CNN产生的伪随机序列周期很长,而且在很长一段时间内是无法预测的,具有很好的随机性。所以,将这两者结合得出的这种混沌加密算法的安全性比以往的普通序列加密算法的要高得多。一般情况下,研究者们应用混沌进行图像加密常用的思路主要有以下3种:第一种是只对图像的像素空间进行位置置乱;第二种是对图像的灰度值进行变换;第三种是将位置置乱与灰度值变换两者相结合。研究表明,任何单一的对图像像素值置乱或对图像像素位置置乱,很难达到很好的图像加密效果。本研究结合CNN和混沌映射的优点,首先提出了一种基于CNN和Chebyshev混沌系统交错产生的伪随机序列的设计方法,然后,再将这种伪随机性能很好的交错混沌序列应用在图像加密过程中。
一、CNN和Chebyshev映射
CNN的应用领域是非常广泛的。当将其应用于保密通信和物理学中时,往往需要网络具有混沌吸引子或极限环解。CNN的动态模型有3元、4元等多种形式,本文中主要研究如下4元CNN动态模型:

式(1)中:xj表示状态变量,ij表示外部输入,yj表示相应的神经元输出函数,并且它们满足如下公式:
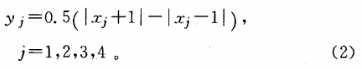
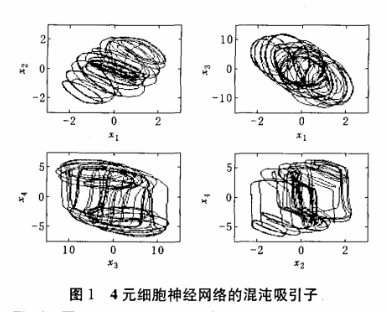
当a4=100,S11 =-1,S13=1,S14=-1,S21=1,S22 =3,S23 =O,S31=14,S32 =-14,S33 =1,S41=-99,S44=100,系统的混沌吸引子如图1所示。
Chebyshev映射是一个典型的混沌系统:
![]()
式(3)中:当-1<xn<1,w≥2时,无论我们把初始值选择得多么接近,反复多次迭代出来的序列都是互不相关的。因为,在此范围内,它是混沌和遍历的,同时具有正交性。
二、PN序列发生器设计
因为计算机自身具有有限字长效应,使得实际产生的任一序列必然具有周期性。所以,我们是无法消除周期性的,只能通过采取措施尽量延长序列的周期。基于这样一种思维和理念,我们提出了一种用CNN和Chebyshev混沌映射交错产生伪随机序列的方法,图2是产生这种混沌序列的结构图。
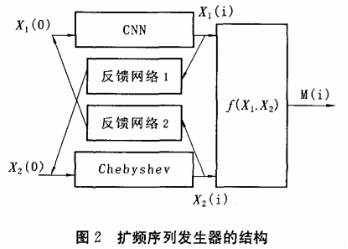
在图2的结构图中,我们对4元细胞神经网络和Chebyshev映射的输出信号进行了反馈处理,因为这两个系统的定义域和值域不一定完全相同,所以,必须通过反馈网络1和反馈网络2把它们转化到各自的定义域中。如果,不采取这样的处理方式,这两个系统的相空间是发散的,是不会收敛的,从而就不能满足系统的要求了。为了得到二值的伪随机序列,我们要对输出的模拟实值序列量化的方法是:在f1(x1,X2)中,先取出实值模拟序列X1(i)和X2(i)的小数部分x1(i)和x2(i),再把x1(i)和X2(i)转化为二进制形式的小数0.b1x1(i)b2x1(i)....bnx1(i)和0.b1x2(i) b1x2(i)…bnx1(i),其中N为二进制的位数,然后取出第j位(1≤j≤N)bjx1(i)和bjx2(i),最后通过运算bjx1(i)和bjx2(i)得到PN序列M(i)。
三、伪随机序列性能分析
下面简单地从平衡特性、自相关函数和互相关函数等方面分析这种序列的伪随机性能。
1、平衡特性
为了分析这种伪随机序列的平衡特性,随机选取了一些不同初始条件、不同长度时的序列进行分析,结果如下表1所示。从表中可以看出,序列中的1和O的数目相差不大,几乎趋于平衡。所以,基于CNN和混沌交错反馈产生的伪随机序列,在整个空问服从均匀分布,具有理想的统计特性。

2、自相关函数
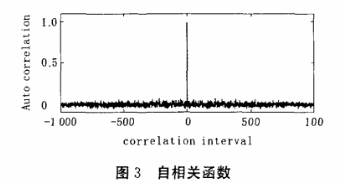
根据Golomb对伪随机序列的假设,理想的混沌序列序列的自相关函数是冲激函数。因此,在这里我们来分析该序列的自相关函数,其仿真结果如图3所示。从图表中可以得知,最大旁瓣是0. 0555,其自相关函数近似为冲激函数。所以,由CNN和Chebyshev混沌映射交错产生的伪随机序列具有理想的自相关函数。
3、互自相关函数
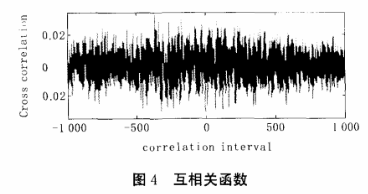
众所周知,由于计算机自身具有有限字长效应,使得实际产生的任一序列必然具有周期性,所以,任何一个混沌序列的周期也是有限的,也就是说明混沌序列的互相关函数并不是精确等于O。该序列的互相关函数如下图4所示,它的最大值为0. 0345,近似等于O。由此可见,该序列具有比较理想的随机特性。
四、图像加密算法设计
假设P代表一幅大小为MXN的明文图像,其中,M和N分别代表一幅图像的行数和列数,Px,y表示在位置(x,y)处的一个像素点的灰度值,其中,1≤x≤M,1≤y≤N,1≤Px,y≤255。为了提高此算法的安全性,同时采用了灰度置乱和位置置乱两者相结合的算法形式。
本文中采用的加密方法的基本流程图如5所示。
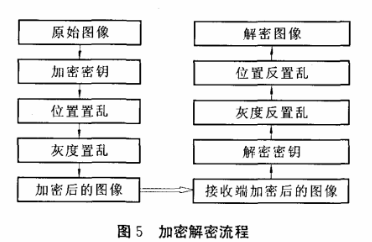
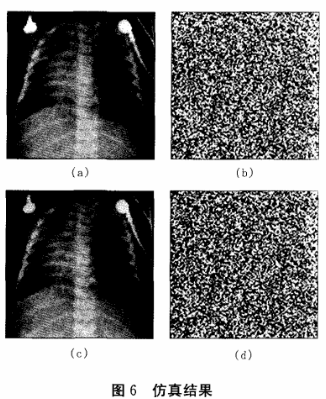
若参数w=2,初始条件X=(xo,yo}是-1~1之间的任意值,这些变量用于控制密钥的产生。选择胸透X线图片图像(400X400)作为仿真图像,利用上述的加密算法将其仿真结果如上图所示。图6(a)为原始图像,图6(b)为加密后的图像,图6(c)为密钥正确解密后的图像。通过分析发现,当其它参数都正确,只是密钥有很细微的差别时,都不能正确解密出原图像,而且看不到原图像的任何信息(如图6(d))。因此,此加密算法具有较高的保密性,同时也表示了此种新算法的可行性。
五、安全性能分析
1、直方图分析
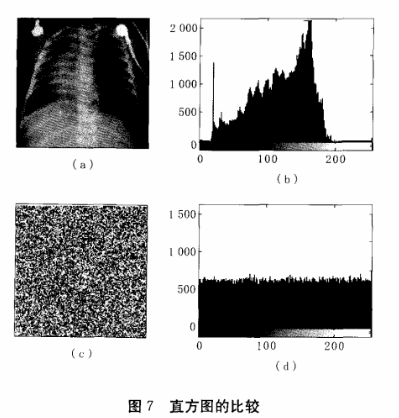
直方图是一种直观描述图像像素值的重要方式,我们通过得到了加密后图像的直方图与原始图像的直方图,如图7所示,图7(b)为原始图像的直方图,图7(d)为加密后图像的直方图。从图中我们发现加密前后直方图的变化非常大,尤其是加密后图像的像素值分布得非常均匀,这样就不能看出原始图像的分布规律了,使得破译者不能从这里找到有价值的信息,即有效地抵制了攻击者的破译。
2、信息熵
图像的信源熵与图像灰度值的分布情况有着密切的关系,即:灰度值分布得越均匀,图像的信息熵就越大;灰度值分布得越不均匀,图像的信息熵就越小。没有通过加密处理的图像,它的灰度值分布一般都是不太均匀的,所以信源熵就很小。通过分析和计算,我们发现,加密后图像的灰度值分布比加密前均匀多了,所以,加密后的图像的信源熵增大了,这就使得攻击者不能从信源熵这方面来获得有用的图像信息。所以,从信源熵攻击的角度来讲,此加密算法是安全的。
小知识之自相关函数
自相关函数(Autocorrelation Function)在不同的领域,定义不完全等效。在某些领域,自相关函数等同于自协方差(autocovariance)。











