Shannon密码理论指出,通过统计分析可以破解多种密码,但采用混乱扩散的方法可以抵抗统计攻击,Chen等将二维Arnold变换推广到三维,提出了一种3D cat映射加密算法,虽然进行多次置乱和混淆,但一旦密钥确定了,对应3D cat映射的矩,阵参数就固定不变,将混沌序列进行量化,再用量化序列进行置乱,量化过程是一个信息损失的过程,这使得解密者无法推测混沌系统的初值。而提出了一种复合混沌系统的思想,产生出4个混沌序列,经异或运算得到新的复合序列,使得解密者无法由破译的加密模板来推测混沌系统。
本文提出了一种改进的3D cat映射,使每次变换后矩阵的参数都发生变化,并综合运用Logistic映射、Chebyshev映射、Chen系统生成的符号控制序列,对图像文件进行加密。
一、混沌系统
1、Logistic和Chebyshev系统
一类非常简单而又应用广泛的混沌系统是Logistic系统:
![]()
在0.569 945 6--μ≤4时,Logistic呈混沌状态,μ∈(O,1),k∈N。另一类是Chebyshev映射:
![]()
其中Xk∈(-1,1),k∈N。
经过简单的变量代换,式(1)等价于:
![]()
其中入∈[o,2],Xk∈(-1,1),入=2时为满射。分析可知,Logistic和Chebyshev具有自噪声、对初始值敏感等特性,这对图像文件加密是有益的。
2、Chen系统
Chen系统表示为:

其中a,b,c是正实数,当a=35,b=3,c∈[20,28.4]时,系统是混沌的。
3、3D cat映射变换
经典Arnold变换是二维可逆混沌映射:
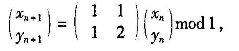
其离散形式为:

其中N为图像的大小,n为自然数。首先将二维离散Arnold映射推广为:
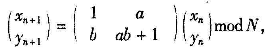
其中a,b为正整数,其中的映射矩阵也是一个保面积的可逆变换。然后通过上述二维映射来构造3个三维映射:
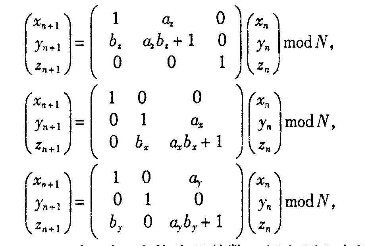
其中ax,ay,az,bx,by,bz均为正整数.记上面3个矩阵分别为A1,A2, A3,可构造A =A1xA2 xA3,则:

称上述变换为3D cat映射,由于detA=1,故3D cat映射为保面积变换。取ax=ay=az=bx=by=bz=1,则:
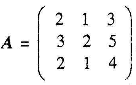
对应Lyapunov指数为σ1=--7.184 2,σ2=0.243 0,σ3=0,572 8。而Arnold变换对应LyapunoV指数为σ1=2,618 0,σ2=0.382 0。Ly8punov指数越大,对应系统的混沌性越强,故3D cat映射(6)要比Arnold映射(5)混沌性强,图1是Amold与3D cat映射对256×256的lena图像加密次数效果图。

采用向德生等计算两变换的置乱度算法,任一像素与四周相邻像素的像素值之差为:
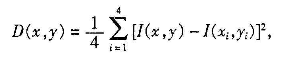
其中,I(x,y)为图像I在(x,y)处的灰度值,(xi,yi)为(x,y)上下左右4个相邻像素,除去图像边缘上的像素外,相加D(x,y)平均即得到整个图像的平均相邻灰度差为:
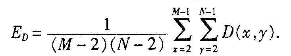
定义灰度值置乱度为:
![]()
其中M,N为图像的行、列数,ED,ED'为分别表示置乱前、后图像的平均相邻灰度差,这样,ED∈(-1,1)值范围.若置乱度小于O,表示置乱效果比原图还差;若置乱度大于0,则表示灰度置乱效果比原图要好,而且越趋近于1越好。
表1列出了两变换对不同大小图像的置乱度η(以256级灰度值,置乱一次为例),表2列出两变换对不同大小图像周期T的比较,表3列出了两变换的加密次数与时间t的关系(以cpu:1.41GHz,内存:5 12为例)。
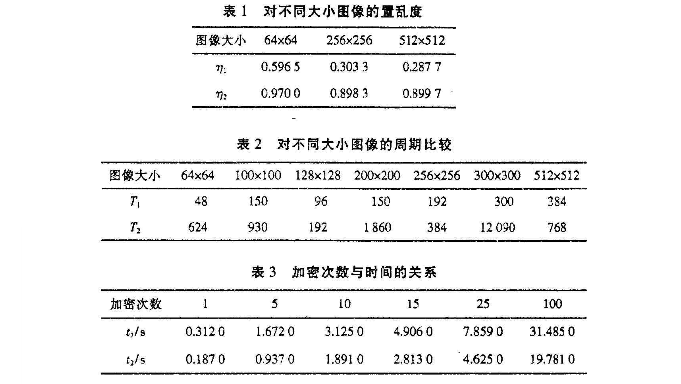
显然,从上面各种角度比较两种变换,3D cat映射比Arnold变换有更好的效果。
二、置乱算法
1、算法设计
本文密钥为x0,Yo,n,这里xo,yo为混沌系统迭代初始值,n为加密次数,首先由Chen系统(4)产生3D cat映射矩阵A的参数,用该映射对图像进行位置置乱。Chen系统的初始值为:
![]()
其中1≤i≤n为置乱次数.这样每置乱一次,对应矩阵A的参数也是变化的,与原来的3D cat映射参数固定相比,增加了矩阵的不确定性,提高了破译难度。
其次由密钥xo通过式(1)生成混沌序列,并转化为符号控制序列:
![]()
再由密钥yo通过式(2)或式(3)生成替换序列{yk},我们按以下规则生成{yk}:

由于此时{yk}并不是均匀分布的,对其作一反余弦变换,即:
![]()
则{yk'}为均匀分布的,将其转化为2k值序列,由此序列再与原图像按位异或运算,便得到加密图像。由于式(8)并非是由一个混沌系统生成,而是两个系统复合得到的,破译者很难根据混沌序列的特点来估计该系统。
2、算法步骤
加密步骤如下:
1)输入图像,记图像矩阵为I,由xo通过式(1)生成混沌,并转化为符号控制序列{xK};
2)由Y0作初值,按式(8)规则生成置乱序列,并转化为2K值序列{yk},本文取k=8;
3)由式(7)生成zo作为Chen系统(4)的初值,生成3D cat映射的矩阵系数,进而与图像作置乱,得到II;
4)由II再与{yk}进行按位异或运算得到III;
5)重复步骤3)和4)n次,得到最终加密图像。
解密过程为上述过程的逆过程,一般对于混沌序列我们不取它的初始部分,会得到更好的加密效果。
三、实验结果
采用本文方法对图像进行加密,图1是对256×256的lena灰度图像的加密结果,所取密钥为双精度xo=0.123 456 789 012 345 6,y0=0.123 456012 345 6789,n=5,加密及解密结果见图2,其中,(a)为原图,(b)为加密图,(c)为正确密钥的解密图。(d)为错误密钥的解密图,所取密钥为xo= 0.1234567890123455,yo=0.123456012345 6789,n=5。可见10-i6的差别便不能正确解密,密钥空间为:1016×1016×28=2.560 0×1034。

图3是与图2相对应图像的灰度直方图(横轴为灰度值,纵轴为像素数),加密图像和错误密钥解密图像的直方图分布均匀,与原图像没有任何相似之处,有效地防止了统计攻击。
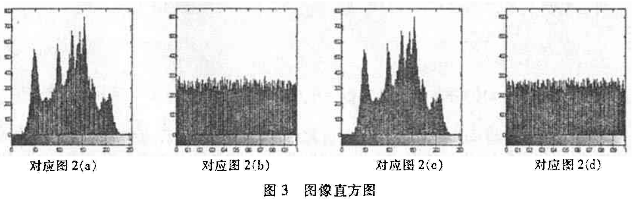
表4列出Chen等m算法与本文算法所生成加密图像与原图相关系数P1,p2的比较,其中Po为原图的自相关系数,可见本文算法更能有效地破坏图像像素间的相关性。
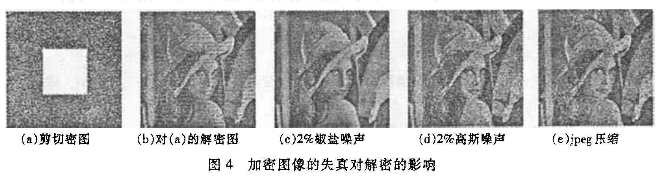
图4是对加密图像进行的攻击试验,其中(a)是剪切密图,(b)是对(a)的解密图,(c),(d)分别是对添加20%的椒盐噪声、2%的高斯噪声的解密图,(e)是对加密图进行jpeg压缩,压缩因子为50%。由图4可知,算法对有损压缩和信道噪声产生的失真具有良好的抵抗能力。
小知识之矩阵
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵,例如稀疏矩阵和准对角矩阵,有特定的快速运算算法。











