二十一世纪,我们正式进入了信息时代,绝大多数信息是由计算机和Internet进行存储和传输,这些信息包括文本、音频、视频等。但不幸的是由于计算机犯罪日益猖獗,就不得不迫使我们把计算机信息安全技术看成现代计算机科学的一个重要发展方向。在这个多媒体时代,数字图像已经渗透进人们生活的各个方面,比如私人图片、商业机密图片、各种重要军事目标的照片等等,所以保证数字图像储存和传输安全已经成为计算机信息安全的一个重要课题。
数字图像要比文本文件大得多,这就要求其加密算法既能有效地抵御各种恶意攻击,又不会有太大的计算量。
数字图像置乱变换是近年来图像加密的常用方法,其又分为图像空域置乱和变换域置乱。现在已有的图像置乱变换技术有:Anrold变换、幻方变换、FASS曲线、Gray码变换、Conway游戏、IFS模型、Tangram算法、Hibert曲线、椭圆曲线、广义Gray码变换等。但它们都有其缺点,比如说空域置乱变换Amold变换:
![]()
通过这一过程将离散化的数字图像矩阵Z中的点重新排列。由于离散数字图像是有限点集,这种反复变换的结果在开始阶段Z中像素点的位置变化会出现相当程度的混乱,但由于动力系统固有的特性,在迭代进行到一定步数时会恢复到原来的位置,即变换具有庞加莱回复性,这样,只要知道加密矩阵,按照密文空间的任意一个状态来进行迭代,都会在有限步内恢复出明文(即要传输的原图像),这种攻击对于现代的计算机来说其计算时间是很短的,因而其保密性不高。再比如一些频域置乱加密算法,虽然其加密效率高,在频域内变动很少的像素点就能达到较好的加密效果,但辩证地从另一方面看,该算法的加密复杂度就降低了,容易受到恶意攻击。
本文就针对以上算法的缺点,利用Logistic混沌序列,提出了一种新的图像置乱算法。
一、混沌系统
混沌现象是在非线性动力系统中出现的确定性、类似随机的过程,这种过程既非周期又不收敛,并且对初始值有极其敏感的依赖性。从时域上看,混沌映射得到的序列类似于随机序列,相关性较弱,具有很好的类白噪声特性,因此可以用来产生伪随机信号或伪随机码。原理上只要增加迭代次数,伪随机码的周期可以很长,产生长码十分简单。通过混沌系统对初始值和结构参数的敏感依赖性,可以提供数量众多、非相关、类随机而又确定可再生的信号。由于上述特点,混沌已广泛应用于保密通讯中,同时也可以作为加密序列。混沌加密技术已成为一种新兴的加密技术。
Logistic序列的混沌特性和统计特性:
Logistic映射是一个源于人口统计的动力学系统,其系统方程可写为如下形式:
![]()
其中Xn为映射变量,μ为系统参量,它们的取值范围分别为:-1<xn<1,0<μ<2。Logistjc映射是一个非常简单,却又具有重要意义的非线性迭代方程,它具有确定的形式,并且系统不包含任何随机因素,但系统却能产生看似完全随机的,对参量p的动态变化和初值极为敏感的现象。
证明系统产生的序列的概率分布函数为:
![]()
其中p(x)是不依赖于初始值的,它对混沌系统具有普遍适用性。人们可以利用概率分布函数来计算混沌系统的均值、自相关系数、互相关系数等统计特性。其中均值为:

自相关函数:
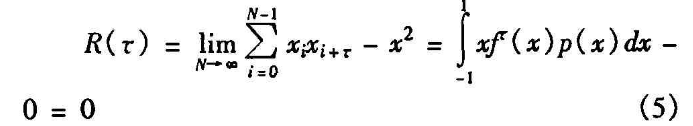
设取两个初始值x0,y0,那么序列的互相关函数为:
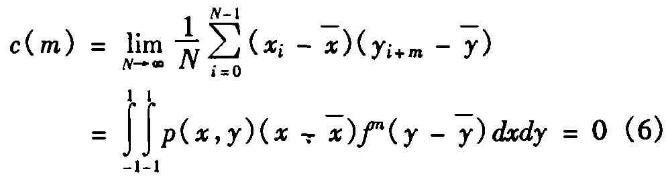
以上特性表明,尽管混沌动力学系统具有确定性,但其遍历统计特性等同于白噪声,因而可以应用于包括数字通讯和多媒体数据安全等众多应用领域的噪声调制。
二、基于Logistic混沌序列的空域加密算法
1、加密算法原理
首先根据式(2)生成一组混沌序列机(密匙为xo)。接着把生成的混沌序列xk整数化,使之生成灰度置乱矩阵G。再对混沌序列钆进行适当间隔的抽样,并整数化,得到整数序列hi,根据参数hi对图像矩阵进行行列置乱处理。
2、具体算法描述
(1)加密算法
第一步:计算图像的大小(像素点的总数),确定混沌序列xk的长度。
![]()
第二步:根据式(2)生成混沌序列Xk,令μ=2。首先,把xk整数化,生成灰度置乱矩阵G,并令其值g∈[O,255],取整算法:
![]()
接着再把xk以某种步长(跟图像大小有密切关系)进行抽样,生成混沌序列Yi(用变步长对xk进行抽样,一是为了扩大Yi之间的差异,增强对密匙x0的敏感性,二是在保证加密效果的前提下降低加密运算量),取整(其算法和每幅图像大小密切相关),生成行列置乱序列hi。
第三步:对原图像进行灰度变换处理。设原图像矩阵为Z,把Z中的每个像素的灰度值对灰度置邑乱矩阵G中相对应的g进行位的异或运算,生成加密图像M,即:
![]()
第四步:对加密图像M进行行列置乱处理。首先对M进行逐行移位,移位参数为hi(每n行具有相同的移位参数,n跟图像大小有关),接着对M进行逐列移位,移位参数为hi(每n列具有相同的移位参数,n跟图像大小有关)。即得到最终加密图像E。
(2)解密算法
首先输入正确的密匙xo,已生成相同的混沌序列xk,及gk和hi。接着进行加密第四步和第三步的逆运算即可。
(3)算法流程图
1)加密流程图如图1所示。
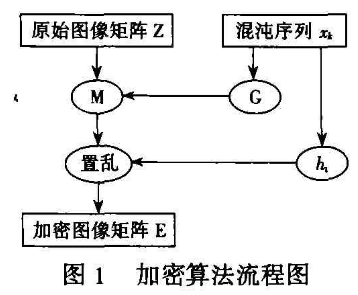
2)解密流程图
解密流程即为加密流程的逆过程。
三、实验结果
1、Logistic混沌序列对初值敏感性的验证
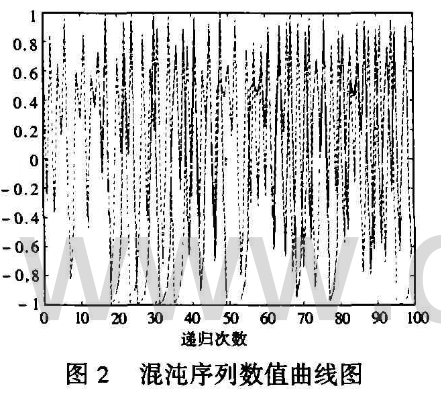
两序列初值分别为:X01=0.800616,x02=0.800617
通过图2可以说明,即使两个初始值xo相差很小(只有0.000001),但n到一定大小的时候,两个xn的起伏就有很大的差别,变得不相关。这个特性就决定了灰度置乱序列gk和行列置乱序列hi,既是随机序列,又对密匙正确与否的判断,具有极高的灵敏度。
2、该加密算法的编程实现
由以上试验可见:图像经加密后,其灰度的真实分布已完全被掩盖。也就是说,恶意攻击者无法从直方图来推测图像的大体内容。
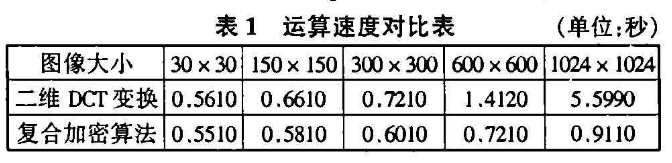
3、该加密算法运算速度的优势
该算法与频域加密算法(这里仅做二维DCT变换)处理相同大小图像的运算速度对比表。(软件环境:MATLAB 6.5 CPU:pentium3 700Mhz)
四、结论
本文提出的基于Logistic混沌序列的图像空域复合加密算法,通过大量实验得到了较为满意的效果,该算法具有以下优点:
第一,本算法是在空域内进行的,相较于其他变换域的图像加密算法,在不降低安全性的条件下能大大减少计算量。例如:wr变换,要进行N/2log2N次乘法运算,NlogN次加法运算。而快速DCT变换所需的运算次数相当于2N的FFT所以在一般分辨率的图像上(1024*104),本算法的快速性就能表现出来。
第二,以上基于Logistic混沌序列的图像空域加密复合算法能有效地克服其他空域置乱算法(诸如:Amold变换、幻方变换等)易受攻击的缺点。因为此种算法的置乱矩阵是随机的,只跟密匙有关,所以就不可能通过差分法等试出置乱矩阵的方法进行解密。此外,该加密算法对密匙正确与否的判断,灵敏度极高。就如实验所示,哪怕输入的伪密匙与正确的相差0.000001,也不能获得解密图像。
第三,因为本算法进行的是双重复合加密,所以就进一步强化了加密图像的安全性。即使破译者知道密匙和生成随机序列的算法,但由于本算法还包含其他的算法因素,就使之几乎不可能在有限长的时间内破解。那些算法因素包括:混沌序列的长度、灰度置乱矩阵的取整算法、灰度值的位运算、行列置乱参数的抽样步长、行列置乱顺序等。
假如能进一步降低运算量,则此种加密算法在视频加密中也有着非常美好的应用前景。
小知识之映射
映射是个术语,指两个元素集之间元素相互“对应”的关系。








