神经网络作为一种自适应建模的工具,具有建立任意未知系统的输入输出之间关系的能力,已经被广泛的应用于各种工程领域。图像加密技术是保证需要进行秘密传输的图像数据在通信网络中安全传输的主要手段。
目前将神经网络技术应用于图像加密主要分为基于Hopfield神经网络的图像加密、细胞神经网络的图像加密、混沌神经网络的图像加密,应用离散Hopfield神经网络生成的序列密码,对图像信号进行加解密,其主要利用网络生成的序列构造置换矩阵对图像矩阵进行位置置换。基于细胞神经网络的高度非线性动力学行为,利用四阶细胞神经网络产生的超混沌序列用于图像加密。建立了一种具有三重密钥的混沌神经网络进行图像加密。但以上IE技术都基于传统的神经网络模型,在同一隐藏层的传送函数都是一样的,常用的函数为S函数,然而这类神经网络在学习过程中存在网络易陷入局部最优,且收敛速度慢等特点。而混沌系统能够很好的应用于信息安全领域,是由于其对于初始条件和系统参数具有强的敏感性,将混沌序列作为密钥流进行图像加密,但是由于单独的混沌系统的另外一些特性如同步性、参数少等,使得安全性不能得到保障。
正交基函数神经网络由于其简单易实现,已被应用于图像处理、非线性过程控制、空气质量预测等工程领域。因此为了克服传统神经网络模型和混沌系统作为密钥的缺陷,文中首次提出基于正交基函数神经网络的图像加密算法,其思路是根据彩色图像结构信息,结合混沌系统,构造出基于Chebyshev正交多项式基函数的神经网络模型,以三个简单的混沌模型产生的混沌序列为输入(这相对于复杂的高维混沌系统而言计算复杂度较低),使用多项式神经网络来建立新的混沌序列,进而以此构建一种以异或运算为基础的像素值替代图像加解密算法。
一、混沌正交基函数神经网络模型
1、混沌模型
所构建的网络模型是需要以混沌序列作为输入的,这里首先介绍3种简单而应用广泛的混沌模型。
1) Logistic模型
Logistic方程:
![]()
其中O< μ≤4,产生的序列xn∈(O,1)。且知当3.5699456<p≤4时,序列表现出混沌特性。
2)正弦平方映射模型
迭代方程为:
![]()
若其初值满足0<x0<1,当γ>1时,其Lyapunov指数大于零,且Lyapunov指数λ=ln(γ),系统工作在混沌状态。
3)组合混沌映射
将Logistic混沌映射和无限折叠混沌映射进行组合可得到一种新的混沌映射模型,其迭代公式如下:
![]()
若取参数b=l,a>10,3. 5699456--<σs4。这样就可以产生(0,1)之间均匀分布的伪随机数。
2、正交基函数神经网络
正交基函数具有很多种,如Chebyshev正交基函数。Her-mit正交基函数等,但为了使神经网络的输出结果易与图像数据的象素值进行运算,这里使用Chebyshev正交基函数作为网络的传输函数,因为其值域在为[-1,1]。
(1)Cbebyshev正交基函数
定义1:Tn(x)=cos(nsrccosx),-1≤x≤1。称为Chebyshev多项式,它是在区间[-l,1]上关于权函数p(x)=1//1-x2的n次正交多项式。由ChebysheV多项式定义可知,应用余弦和积功是可得到Chebyshev正交多项式的递推公式如下:
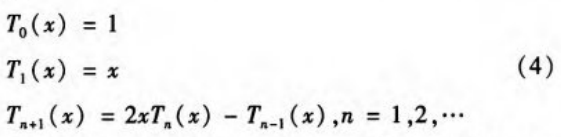
由式(4)所定义的Chebyshev多项式函数称为Cheby8hev正交基函数。根据其定义,易得知Cheby8hev多项式Tn(x)的最高幂xn项的系数为2n-1,且当x∈[-1,I]时,|tn(x)|≤1。
(2)基于Chebyshev正交基函数的神经网络建模
为了产生应用于彩色图像加密的密钥流,构建一个多输入一多输出神经网络模型。考虑到彩色图像具有R、G、B三个分量,且为了增强安全性,为此构建一个3-n-1的网络模型。可以应用其产生三组输出,作为加密各分量的密钥,而每组输出所对应的输入是由上节所提到的三种混沌模型产生的混沌序列,其网络模型如图1所示。
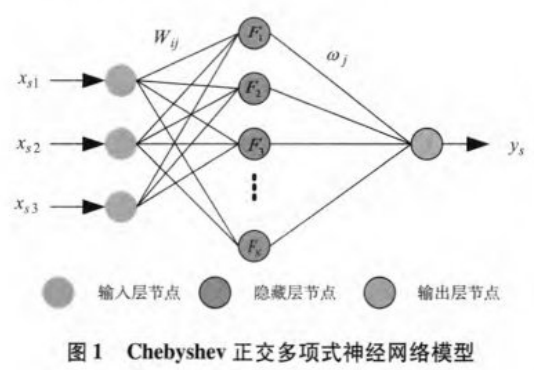
其中xs=(xs1,xs2,xs3),s=1,2,3,,..S为输入的混沌序列,S为参与训练的样本数。xs1,xs2,xs3分别是由上节三种混沌模型所产生的混沌序列值。Wi,j为输入层节点到隐藏层的权值,Wj为隐藏层到输出层的权值,输入层和输出层的神经元的激励函数均为恒等映射,所有神经元的阈值均为0。隐藏层神经元的激励函数为由式(4)所定义的一组正交基函数,记为Fj(.),j=0,1,2,...,N。
根据以上构建神经网络模型,可得到该模型中各层的具体表示如下:
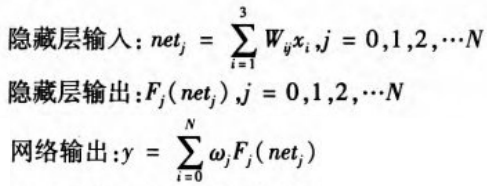
其中N为隐藏层节点个数,设在网络训练过程中所采用的样本对为(xsf(Xs)),其中xs=(xs1,xs2,xs3).s=l,2,3,...S,S为训练所使用的样本数。因为在训练阶段需要知道期望输出,在此定义期望输出为:
![]()
由此可定义输入输出误差为:es=fs(xs)-ys,网络训练的代价函数为:
![]()
根据梯度下降算法可得到网络中权值的更新迭代公式如下:
![]()
其中:
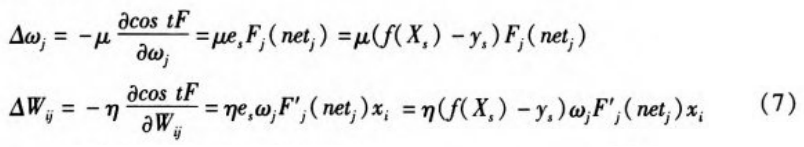
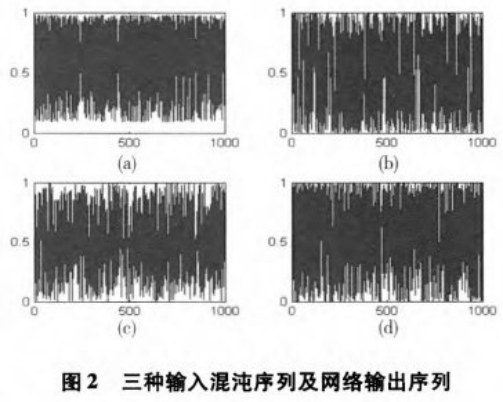
在Chebyshev神经网络模型中,由于采用了较为复杂的Chebyshev正交基函数作为非线性激励函数,因此当该网络逼近复杂非线性目标特性时,相对于传统的神经网络模型可以采用较少的隐藏层神经元。图2给出选用1000组输入混沌序列及得到的网络输出序列,其中(a)(b)(c)分别为前面所提到的三种混沌模型所产生的序列,而(d)为网络的输出序列,从图中可知网络的输出序列也具有很好地混沌特性。
二、加密解密算法
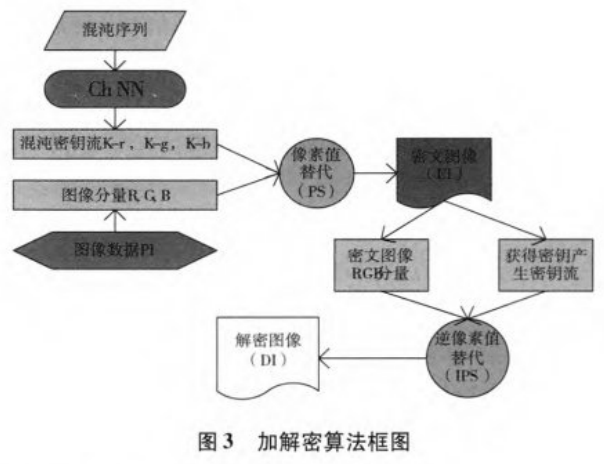
图像加密算法主要分为像素位置置乱和象素值替代,以及两者的混合方法。本文在这里结合神经网络所产生的混沌序列模型,构造一种象素值替代加密模型。其主要包括基于多项式神经网络的混沌序列产生和象素值替代两个过程。加密解密框图如图3所示。
加密算法
设PI( Plaintext Image)为一副大小为MxNx3的明文彩色图像,对其实施加密解密的算法过程为:
Step1:使用前面混沌模型产生的混沌序列作为Chebyshev神经网络的训练样本,构造输入一输出对fs(xs),确定网络的权值Wij和wj。
Step2:再任选混沌初值和参数产生用于网络输入的混沌序列,如式所示。
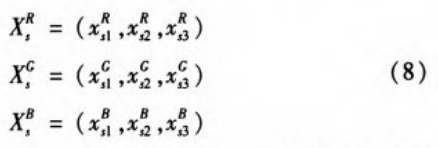
其中xsr,xsg,xsb分别是用于产生加密各分量的输入混沌序列,结合训练过程中所确定的权值wij和wj,根据网络模型产生新的神经网络混沌序列YR,YG,YB。
Step3:为了与图像数据进行运算,将新的混沌序列进行修正,如下式所示:
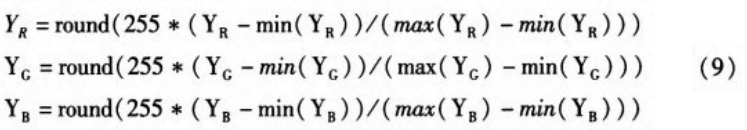
其中round(),max(),min(),分别表示数据取整运算,取最大最小值。
Step4:将图像数据进行分解,分别提取其R、G、B分量,分别记为IR,IG,IB分别按如下式进行像素替代变换,得到各分景的加密结果EIR,Elc,EIR( Encryption Image, EI):
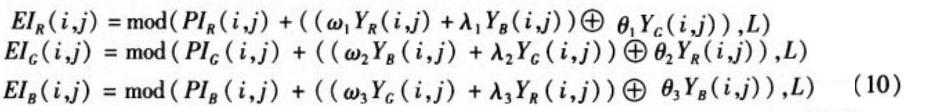
其中wi,λi,θi(i=1,2,3)为任意的整数,其中L=255。
由以上算法描述可知加密过程中的密钥包括混沌模型的初值,网络训练过程中得到的权值,还包括这三组正型参数,这样便极大的扩充了密钥空间,增强了安全性。密钥可表示为:
![]()
其中C,W,I分别为:
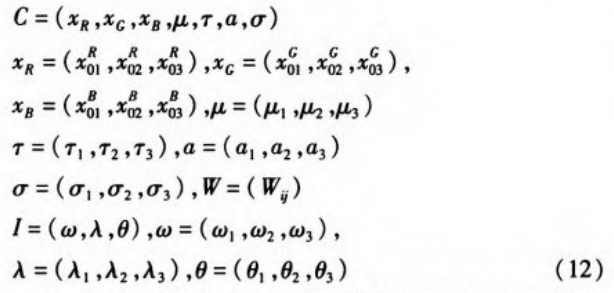
其中XR,XG,XB分别为产生三组网络输入的混沌系统的初值。
Step5:将EIR,ElG,EIB进行重构就可得到密文图像EI。
2、解密算法
Stepl:由秘密信道接收到建立的网络模型及式(12)所定义的密钥,得到加密过程中所用到的神经网络混沌序列;
Step2:如式(8)所示对上述产生的混沌序列进行修正;
Step3:密文图像EI进行解密。分解EI提取R、G、B分量,按式(13)进行解密,得到各分量的解密结果DIR、DlG、DIB。
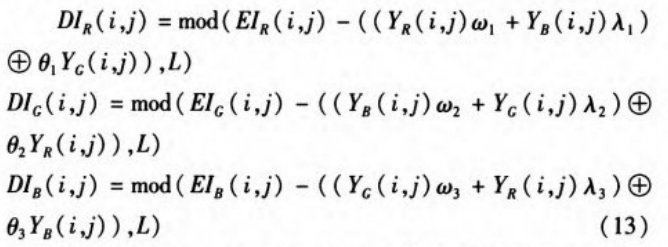
Step4:将DIR、DlG、DIB进行重构就得到解密图像DI(Decryption Image,DI)。
三、仿真与分析
对于一个良好的图像加密算法来说,不仅要在视觉效果上看不到密文图像与明文图像的相似之处,而且更重要的是要具有强的安全性,也就是不易被破解,从而防止信息的泄漏。所以这里从加密结果和算法安全性两方面对所提算法进行仿真分析。
1、加密算法结果分析
为了验证算法的可行性,选取三种混沌模型的初值和参数,产生出用于网络训练的序列值,根据网络模型对训练样本对进行训练得到网络的权值,再根据式加密算法中所描述的产生相应的混沌序列,结合训练得到的权值获得用于加密的密钥序列YR、Yc、ko在Matlab7.0环境下,按照前面所述的方法对两幅彩色图像Strawberry. jpg和Airplane.jpg进行加解密试验。其密钥为:
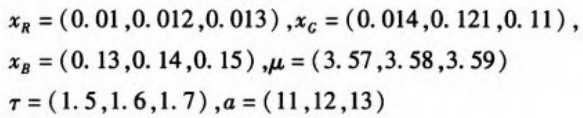
而权值是由训练样本中所使用的混沌序列确定的,其参数值C= (0.01,0.12,0. 13,3. 571,1.565,11,3.571)也可以作为密钥。图4给出了两幅图像的加解密结果。从加密结果(b)、(e)不难看出已经达到了加密的视觉效果,密文图像已完全是一幅杂乱无章的噪声图像,已经不能获悉明文图像的任何信息。

为了定量的分析加密的效果,计算出密文像素变化率(Ciphertext Pixel Change Rate,CPCR)进行分析。由于图像为彩色图像,所以分别计算出各分量的CPCR。如下式:
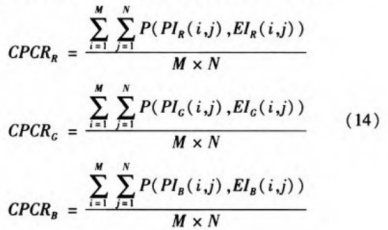
其中,
![]()
可定义
![]()
经计算加密后的图像像素变化率CPCR=99.88%,从而可知加密效果非常好,达到了预期的目标。
2、加密算法的安全性分析
一种优良的加密机制应该是要对密钥具有敏感性和拥有大的密钥空间,就可以有效的抵制群举攻击。
(1)密钥空间分析
由算法描述,可知,在每生成一个密钥序列时,需要使用三个混沌模型分别产生相应的序列作为网络的输入,因此每个混沌模型需要使用3次,如式(12)可知在加密算发中共需要31个密钥参数,其中整型9个,双精度22个,每个双精度浮点型产生的密钥空间约1016,因此加密算法具有非常大的密钥空间,且也可以网络进行训练迭代的次数作为密钥。
(2)钥敏感性测试
为了验证加密算法对密钥的敏感性,在解密时只将生成YR的初值xol做了相处10-7的变化,而其它密钥均未改变。图5给出了的加密结果和解密结果,发现解密结果也是所期望的,其是一幅毫无纹理的噪声图像。这说明了算法对密钥具有很强的敏感性,这也就体现了密码学中所要求的混淆和扩散的目的。

(3)统计分析
抵抗统计分析攻击也是衡量一种加密算法有效性的标准。对于图像数据而言,需要通过加密算法减小相邻像素间的相关性,进而可以减小其受统计分析攻击的风险。
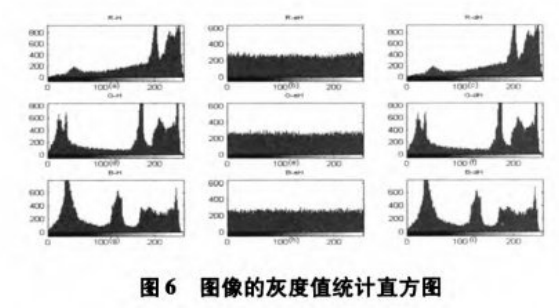
1)图像的灰度值统计直方图
图像像素的灰度统计直方图表明了像素的分布性。图6分别给出了Strawberry. jpg的明文图像,密文图像和解密图像的各分量的灰度值统计直方图。由(b)(e)(h)可看出密文图像的各分量的直方图显示出很大的均匀性,灰度值均匀的分布在[0,255]范围内,这一结果掩盖了明文的分布规律,增强了抵抗统计分析攻击的性能。而PI和DI的直方图基本保持一致,说明了加密算法具有良好的对称性。
2)相邻像素的相关性
较低的相邻像素的相关性也是检验加密算法性能的一个指标。为了检验加密算法仿真中明文图像PI和密文图像EI的相邻像素的相关性,只在Strawberry. jpg的R分量中选取500对相邻像素,来比较它们的相关性,包括水平,垂直或对角的。
图7给出了PI和EI的平行和垂直方向的相邻像素的相关系数图。从图(a)(c)中可以看出明文图像的相邻像素具有较强的相关性,而(b)(d)则显示出EI中相邻像素的相关性较低,基本呈均匀分布的形式。
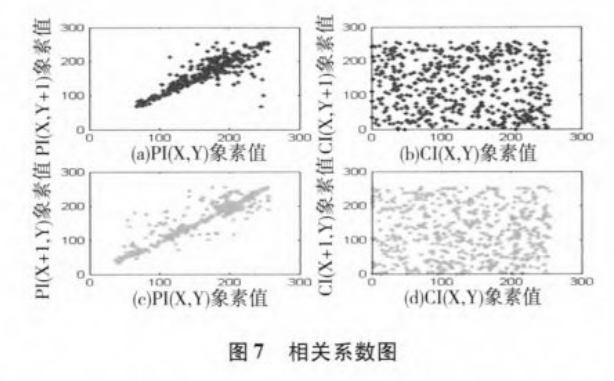
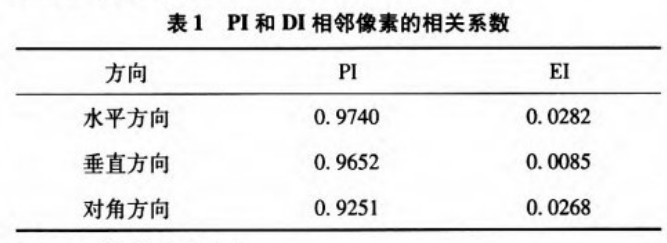
表1给出了PI和Dl在水平,垂直和对角线方向的相邻像素的相关系数。由计算结果知,PI的相邻像素的相关性非常高,接近于l,而DI的相邻像素只有接近于0的相关系数,说明已经完全打破了PI的相邻像素相关特性,PI的统计特征已扩散到DI中。
(4)抵抗恶意攻击
恶意攻击是第三者企图破坏密文图像的一种方法,有效的抵抗恶意攻击也是衡量算法性能的标准。图8给出了Strawberry. jpg受加椒盐噪声攻击和随意涂写的图像及其解密结果。可看出解密结果虽然受到一些噪声颗粒的影响,但PI的轮廓信息还是很清楚的,可以获知需要了解的信息。

小知识之正交基
若向量空间的基是正交向量组,则称其为向量空间的正交基,若正向向量组的每个向量都是单位向量,则称其为向量空间的标准正交基。









