信息安全在网络通信、多媒体系统、医疗图像、远距离医疗等许多领域起着至关重要的作用。近年来,吸引着越来越多研究者的关注。置乱一扩散机制为一种最常见的图像加密机制,在这种机制中排列和扩散被认为是两个独立的阶段,它们都要求扫描图像以获得像素值:排列阶段改变图像像素的位置,但不改变它们的值;在扩散阶段,像素的值发生一系列修改,以至于某一像素值的微小变化都将扩散到几乎整幅图像。整个排列一扩散过程重复一定次数以达到安全性水平要求。因此,在排列和扩散阶段的控制参数成为算法安全性与复杂性的决定性要素之一。
一个好的加密算法应该是密钥敏感的,并且密钥空间应该足够大以抵抗暴力攻击。混沌变换所具有对参数和初值极端敏感的基本特性和密码学的天然关系,使应用混沌系统生成密钥及参数成为安全通信领域一项非常重要的研究课题。由于神经网络的复杂性和时变结构使其作为信息保护的另一选择被广泛的应用,包括对数据的加密、认证、入侵检测等。结合了神经网络与混沌,混沌神经网络(CNN)兼具二者的特性。较传统的混沌映射而言具有更为复杂的时空复杂度,其良好的置乱和扩散特性已经成功用于密码是设计。
本文设计算法使用混沌复合映射控制参数以进行图像置乱。分离输出信号的三个色彩分量使用三个神经元的Hopfield混沌神经网络预处理图像加密,得到置乱密钥流。此处有两个不同初始条件和参数的复合混沌映射分别被用于生成排列阶段控制参数和生成混沌神经网络系统的控制参数。
一、复合混沌映射与混沌神经网络模型
1、复合混沌映射
由Logistic映射的稳定周期3轨道经历倍周期分岔过程可知,帐篷映射Xn的值始终处于(0,1)上,因此,将帐篷映射的方程代人到Logistic映射中,便可以得到一个新的映射TLM:
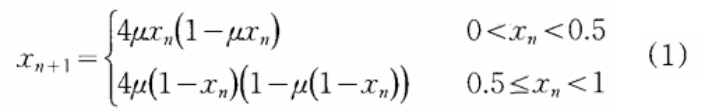
μ∈[o,2],xn∈(o,1)。其混沌吸引子分布如图1。
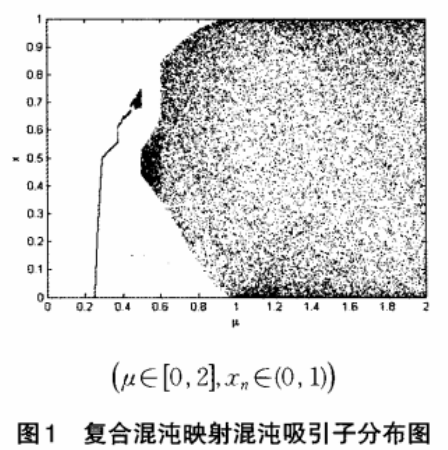
计算TLM映射的Lyapunov指数在μ=0.37--开始恒大于O,而不存在抛物线映射那样间或出现小于O的情况,也就是说μ从0.37变化到2的整个区间上,映射不存在倍周期的窗口区域,从而始终处于
混沌状态。
2、Hopfield混沌神经网络模型
描述Hopfield混沌神经网络模型如下:
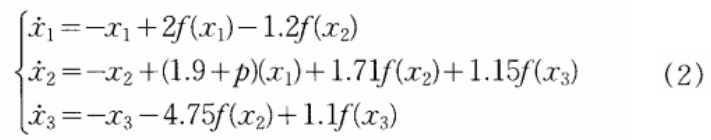
其中,f(x)=tanh(x)
其混沌吸引子分布如图2。
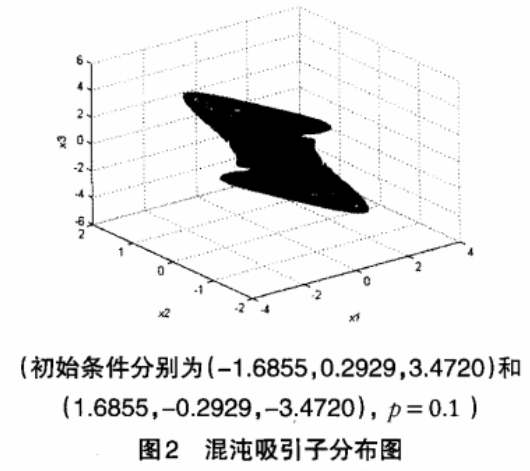
二、图像加密解密算法
本加密算法由置乱和扩散两个阶段构成,其中,由复合混沌映射生成Cat映射的控制参数被用于置乱阶段,该TML映射的参数和初始条件分别称作MTL1和XTLl(O)。TML映射迭代m1次生成Cat映射的控制参数,在稍后的部分进行描述。MTL1和XTLl(O)和m1是本算法的三个加密密钥。在扩散阶段,Hopfield混沌神经网络作用于三个色彩序列信号输出用于改变像素的值(图像均衡化),进行图像扩散。本设计方案中,TLM映射使用不同的初始条件和控制参数称为XXL2(0)和MTL2用于生成高阶混沌系统的初始条件。在扩散阶段,TLM映射分别迭代mr,mg,mb次,得到Hopfield神经网络的三个初始条件。与第一逻辑映射相似,XXL2(0)和MTL2,以及mr,mg,mb也作为加密密钥。由Hopfield神经网络生成密钥流用于图像均衡化,将在本部分的其余部分进行描述。该置乱一扩散过程重复R次.R也作为加密密钥。加密算法流程图如图3所示。
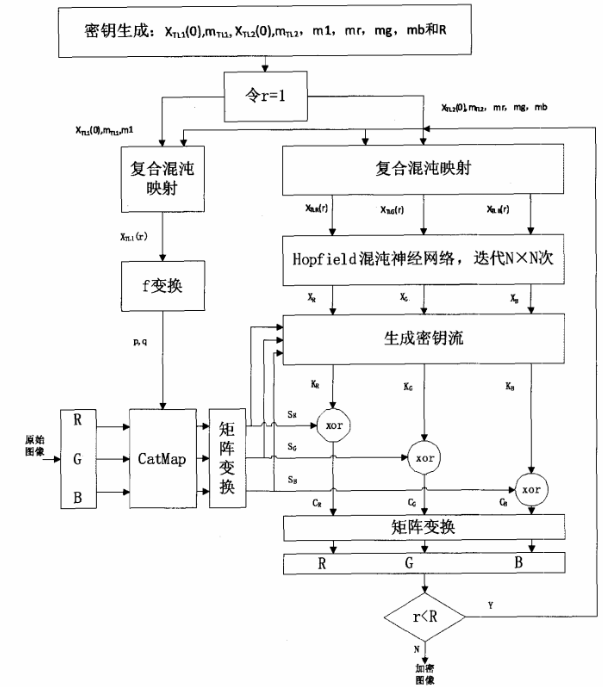
令原始图像为NxNx3的彩色图像,安全密钥分别为:XTLl(O),MTL1,XTL2(0),MTL2,mi,mr,mg,mb和R,r=1。
提取原始图像RGB三个分量,将原始图像转换为矩阵DRDGDB。
以初始条件XTLl(O)迭代TLM映射m1次,得控制参数XrLl(r);以初始条件XTl.2(0)迭代TLM映射mr,mg,mb次,得控制参数XrLR(r)XTLG(r)XTLB(T),分别用于置乱和扩散阶段。
在排列阶段,使用可变参数Cat映射,Cat映射的方程定义为:
![]()
由于det(A)=1,控制参数p,q如下式描述:
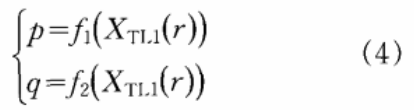
其中:
![]()
![]()
其中D=[DR DG DB]T,分别为NxN的方阵。fatmpa(.)为(7)式所示置乱方程,E=[ER EG EB]。
将置乱图像的像素按照从左到右从上到下的顺序重排矩阵得到序列得:
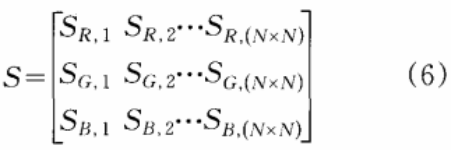
在扩散阶段,令X=fhopfiels(XTI2),其中,fllup/teld(.)为等式等式(2)描述的Hopfield混沌系统。XTL2 =[XTLR XTLG XTLB]T,为系统初始条件。迭代该系统NxN次实现图像均衡化,得X序列:
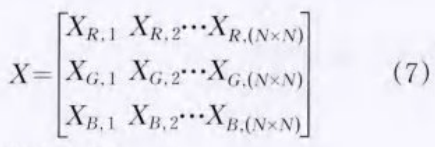
生密钥通过下式求取:
![]()
其中S初值Si,o=127,i∈(R,G,B),j=1,2,….(NxN),K为3x(NxN)的矩阵。
将置乱图像通过以上密钥流进行加密,得密文:
![]()
其中,I∈(R.G,B),J=1,2,...,(NxN),C为3x (NxN)的矩阵,bitxor(x,y)返同两个整数x和y的位异或值。
矩阵C的每一行均为lx(NxN)的行向量,将其进行矩阵变换,转化为(NxN)的矩阵以获得加密图像的三个色彩分量,在将其合成彩色图像。判断当前轮次是否为最后轮次(r<R),若不是返回,循环执行加密过程;否则,得到最终)加密图像Cfinal。
解密阶段为加密阶段的逆过程A由此,将反转的扩散和排列行为分别应用在加密图像上。
三、性能分析
一个好的加密过程应该足密钥敏感的,并且密钥空间应该足够大以抵抗暴力攻击。同时它也应该足够健壮以抵抗各种密码分析和统计攻击。在这一部分,对于本设计图像加密算法及行了安全性能分析以及统计和敏感性分析口分析表明,本密码系统可以f求护密钥和明文以抵抗各种常见的攻击。其中包括已知明文攻击,选择明文攻击,密钥空间,直方图研究,密钥敏感性分析,加密图像信息熵,加密图像相邻像素相关性分析。
1、已知明文和选择明文攻击
式(8)所示扩散密钏矩阵K不仅仅依赖于加密密钥(复合映射的初始值和控制参数,迭代次数R和m,以及高阶混沌细胞神经I蜘络的初始条件),而且还依赖于原始图像本身。因此,即使是相同密钥对于不同图像进行异或操作,该阶段密钥流也是不同的。除此之外,由于渐钥流是可变的,通过返回给加密系统一个黑图像进行密码分析是无效的。由于排列阶段的控制参数和扩散密钥流部足明文图像相关的。所以,本算法可以抵抗已知明文攻击和选择明文攻击。
2、密钥空间
本加密算法,使用两个复合映射初始值和控制参数作为密钥。假设每一个密钥小于10则精确度为10-14,密钥空间为1056。而且,迭代次数R和m也都用于密钥。考虑该密码,密铡空间足够大以抵抗各种暴力攻击,建议密钥空间密钥该至少264才能够抵抗器力破解攻击达到安全水平。
3、统计分析
本部分敏感性分析刚于研究算法的性能。为展示模型的可行性,我们使用256x256的“Lena”图像作为明文图像。加密密钥为:
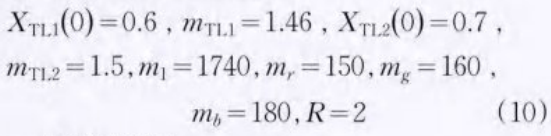
(1)直方图分析
一幅图像直方网描述的是像素密度分布于它们的色彩强度水平的关系。原始明文图像,加密图像的直方图分别由图3和图4给出。如图所示,加密图像的直方图为均匀分布,具有很好的统计特性类似白噪声。因此不能从加密图像中获取原始图像像素的相关信息。因此,本算法不会为任何统计攻击提供任何线索。

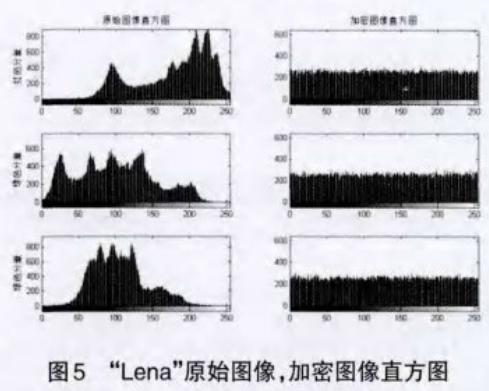
(2)密钥敏感性
为了说明本算法的密钥敏感性,在等式(10)的相同条件下进行试验。对密钥进行细微调整。本例子中,分别将密钥中的XTL1(O),XT12(0),mtl1,mt2分别与原密铜柑差10-14密钥变化如下:
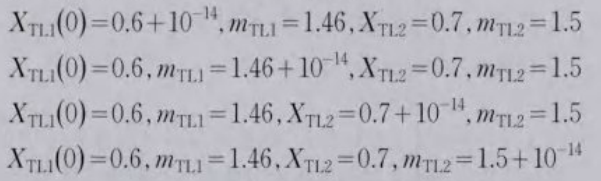
图6所示为Lena罔像使刚这四种情况解密的结果。可见,即便密钥只有微小的差别,解密图像也是与明义绝对不同的,直方图依旧是随机性的。因此,这是因为本算法的高复杂性和高阶混沌特性。

(3)信息熵分析
此处,执行了该设计加密解方法的实验以及分析加密图像图4。“Lena"加密图像信息熵。对于加密图像,计算像素灰度值的信息熵H(m)=7.9551,由AES算法加密图像的值为H (m)= 7.91。本算法的信息熵一诈常接近于理想值8。结果表示,加密刚像接近于随机信号源,可以安全抵抗熵攻击。
(4)相关系数分析
相邻像素之间的低相关性是另外一个优秀加密的特征。栩关系数rxy为图像灰度值的一组相邻像素对(xi,Yi,i=1,2.….Ni)。可以通过下面的公式:
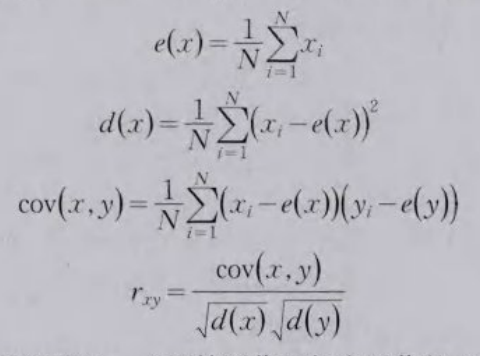
随机选取“Lena”原始图像和加密图像的4000对水平相邻像素,垂直相邻像素,以及对角相邻像素的相关性,由图7所示。显然本算法破坏了相关性的有效性,该图像加密算法有很慢的抵抗统计攻击的能力。
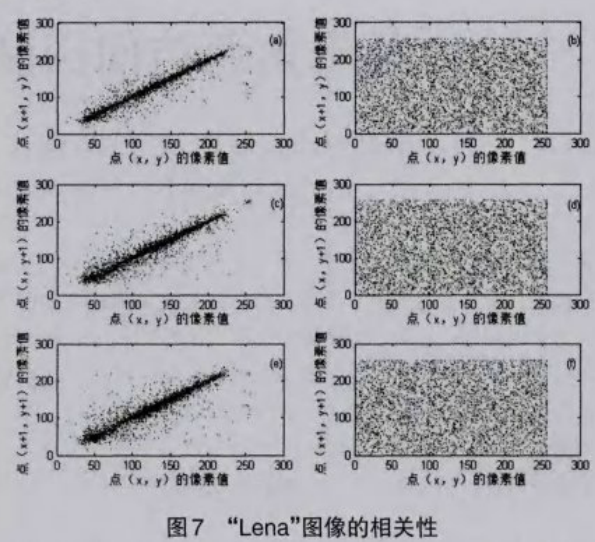
由图中数据可见,原始图像的相邻像素之间有很高的相关性。而加密图像相邻像素之间的相关性几乎可以忽略不计。
小知识之吸引子
吸引子是微积分和系统科学论中的一个概念。一个系统有朝某个稳态发展的趋势,这个稳态就叫做吸引子。吸引子分为平庸吸引子和奇异吸引子。
例如一个钟摆系统,它有一个平庸吸引子,这个吸引子使钟摆系统向停止晃动的稳态发展。









