基于混沌数列变换的图像加密算法

针对现有的数字图像加密算法存在算法复杂、运算成本大以及安全性不高等问题，提出了一种基于混沌数列变换的数字图像加密算法。该算法通过对Logistic和Hybrid两种不同的混沌序列进行变换，从像素灰度值以及像素位置两方面对图像进行加密。

一、序列及变换

1、两种混沌序列

混沌序列作为一种伪随机序列由于具有遍历性高、对初值敏感等特性被广泛应用于数字信息的加密中，本文通过对两种混沌序列的不同变换达到图像像素点位置变换和灰度值变换两方面的目的从而实现对数字图像的加密操作。这两种混沌序列分别是Logistic混沌序列和Hybrid混沌序列。首先，Logistic序列是混沌系统中很有代表性的混沌映射，它被广泛应用于混沌应用中，其定义如式(1)所示，其中初值和参数的设置为O<μ0≤4，0<x0<1，k∈N，由此数列所得的混沌序列xk在[0，1]之间无规律地震荡变化：

第二，Hybrid序列是一种新构造的序列，该序列利用构造的Hybrid混沌映射，通过周期性改变混沌迭代初值来产生混沌伪随机序列。该映射定义如式(2)所示：

此映射不但继承了Logistic映射产生方式简单易行和混沌效果理想等特点而且还能增加了混沌系统的安全性。该映射的参数取值为0<xo<1，O<u1<4，0<u2<4，O<b<l，k∈N时产生序列的混沌效果最好，与Logistic序列不同的是，此数列的产生值在[-1，1]间以x轴为对称轴震荡变换。两种混沌系统的相同点是，在初值相差甚微的情况下，当k大于一定值时，所得zt均会出现很大的差别，这个特点充分体现了混沌系统对初值敏感的特性，使安全性得到了提高。

2、序列变换

由于数字图像可以看作是由每一个像素点所组成的一个二维矩阵，能够实现对二维矩阵的变换即可达到对图像的加密目的，因此，本文旨在将上文所得的混沌数列进行矩阵变换来实现对于数字图像每一个像素点的灰度值置换加密和整体图像像素的位置混乱。首先，针对图像具体像素点的灰度值变换（图像灰度值在0-255之间）问题中，采用第一个Logistic数列变换实现。本文所提出的加密方法需要一个与待加密图像等大的二位矩阵来进行与原图像的异或处理。由于Logistic混沌系统产生的数列值在O到1之间，为了达到数值的范围要求，该变换的方法为将所得的每一个数列值扩大然后对256取模，这样可以保证所得随机整数数列在0至255之间变换，根据图像的尺寸将所得随机数列转换成为同等大小的二维整数序列，计算方法如式(3)所示：

式中：xk-Logistic变换所得序列，yk-所需的异或矩阵元素值，由于本文所做实验针对的图像像素灰度值为O-255所以对256取模，对于其他种类图像的加密可以根据具体图像的灰度信息改变取模值。通过式(3)的变换即可保证每个异或值在0至255之间，然后将所得到的新数列构造成适应图像大小的二维矩阵。

第二种针对Hybrid序列的变化是用来实现像素位置的混乱处理，该加密方法所要达到的目的及根据矩阵乘法，达到对行列两方面的变化。在这个过程中需要构造这样的置换矩阵，所以对单位矩阵的置换规则通过Hybrid混沌映射实现。因此根据Hybrid的伪随机特性可以构造一个置换群对单位矩阵进行变换进而实现对二维图像的加密操作。

定义1 设数列∞是由Hybrid混沌系统产生的一维随机序列，则Hybrid随机置换群GH为：

且k∈N，其中nk为将xk，升序排列后所对应的序列号。

此定义的应用在于通过Hybrid混沌映射产生的置换群可以对单位矩阵的行顺序进行置换，这样就能够构造出所需要的置换二维矩阵。例如取xo=0.76，u1=1.7，u2=2.2，b=0.79的Hybrid映射时，所得的6元置换群为：

如图1所示，通过这个置换群就可以把单位矩阵(a)转化成置换矩阵(b)。

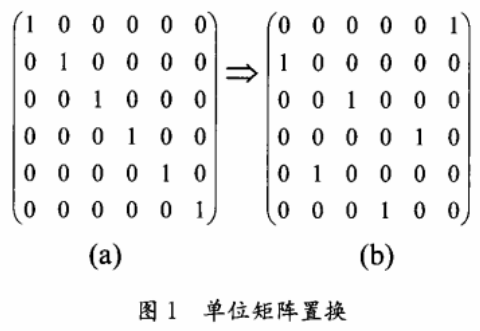
这两种对于混沌序列的变换方法在加密方法中起到了重要的作用。

二、加密算法

1、加密过程

本文提出的数字图像的加密算法分为两个步骤：第一步；灰度值加密，具体步骤为将原始图像的每个像素点的值同上述所得取模后的矩阵进行按位异或处理。设待加密数字图像A大小为m*n，异或矩阵W由式(3)的yk构成，t（m，n）代表异或后的图像像素值，则异或过程如式(4)所示：

该步骤中异或处理是将十进制整数变换成二进制数进行对应像素点的按位异或。异或后将结果转换成十进制数构成加密图像。

第二步，像素位置置乱变换。该变换具体实现是对于异或后图像进行一次位置置乱变换。利用混沌序列构成需要的置换群，通过置换群将符合图像大小的单位矩阵的行顺序进行置乱变化，设图像A尺寸为m*n，根据定义1选择不同的初值和参数构成大小为m元和n元的置换群，分别用这两个置换群将大小为m*m和nxn的单位矩阵E1和E2进行行置换处理从而得到所需要的置乱行列矩阵Em和En，该步骤的加密过程如式(5)所示，E代表此步骤加密后的图像．Ef代表通过式(4)的运算所得t(m，n)构成的矩阵，则位置变换加密过程为：

综合以上两步骤，所得的图像E就是最终的加密图像。

2、解密过程

由于按位异或和矩阵乘法均具有可逆性，所以此算法的解密算法也分为两步，是上述方法的逆运算，首先将加密后的图像E进行位置还原，设矩阵Et'为位置还原后的图像矩阵，根据行列式的性质特征以及矩阵乘法之间存在可逆变换关系，所以该步骤如式(6)所示：

此时，图像Et'像素位置已经恢复到原始图像的位置，再对图像进行灰度值的异或处理即可完成图像重建，u(m，n)为还原后图像的像素点灰度值，如式(7)所示：

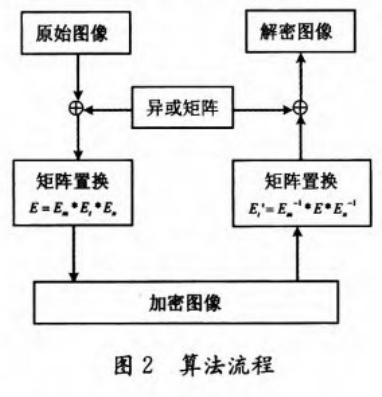
从上述公式可以看出，图像加密和解密是一个对称的逆过程，整个加解密过程可以归纳成一个图像处理系统如图2所示。整个算法的加密解密均分为两步且对称，其中在像素点的异或处理中使用的异或矩阵为同一个矩阵。

三、仿真实验结果

该部分将算法进行了仿真模拟实验，应用matlab软件作为开发工具编程实现了所设计的基于Logistic和Hybrid映射数列变换的数字图像加密算法从而充分验证了算法的可行性。本实验分别针对不同尺寸、形状的图像以及彩色图像进行实验，如图3、图4、图5分别列出对256* 256的lenna图像、533*400大小的风景图和RGB彩色图像进行的加密算法和解密算法的实验结果。三幅图中图(a)表示原始图像、图(b)表示加密后的图像、图(c)为解密图像，从所给实验结果图可以看出，此算法使用范围广泛，对于不同尺寸的图像均可达到加密和解密目的，而且该方法不仅适用于灰度图像。RGB的彩色图像同样可以用该方法进行加密并且加密效果良好。从图(b)加密图像看不能从加密图像中辨识出原始图像信息，而图(c)证明该算法的解密部分能够将原始图像成功还原出来，解密图像效果良好。

四、攻击操作

1、统计攻击分析

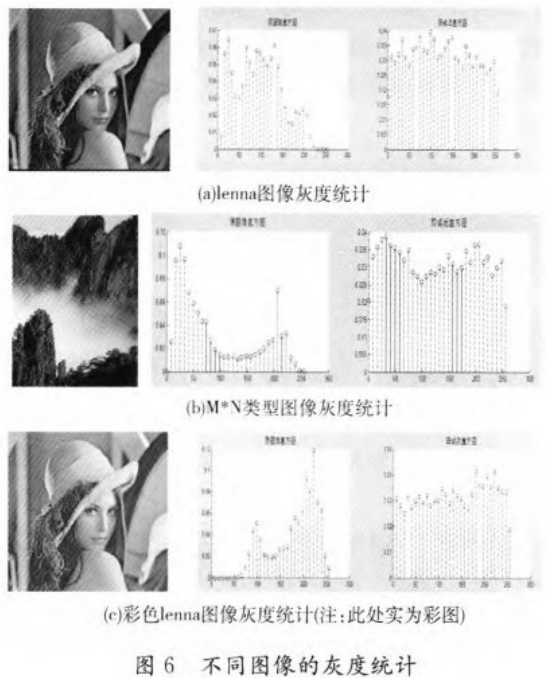
从图像统计分析角度分析，图像的统计信息在一定程度上可以曝露出原始图像的灰度值分布规律，所以能否改变原始图像的统计分布也是图像加密至关重要的指标。该算法的第一个步骤提到的对于图像灰度值的异或目的即是为了抵御攻击方进行灰度统计攻击。如图6所示，从实验结果可以得出，由于进行了异或处理的步骤，使所得加密图像灰度分布非常均匀，使攻击者不能够分析出原始灰度值分布范围，进而增加了算法的安全性。

2、切割攻击

切割攻击是图像信息传递过程中常遇到的攻击操作，收到此类攻击后图像部分信息缺失，使得图像恢复过程受到阻碍，本实验旨在对加密图像进行了切割操作的基础上仍然能够将图像恢复出来。如图7所示，根据控制变量思想，图7 (a)、图7(b)的为对加密所得图像进行不同位置的切割，图7 (c)、图7(d)是对其他尺寸图像和彩色图像进行的变换。第一行显示的是加密图像切割的位置以及切割之后的效果图。第二行显示的是恢复图像的效果，从中可以看出，切割操作对于图像恢复并没有造成很大的影响，原始图像主要信息可以被恢复，辨识度很高而且效果良好。

3、噪声攻击

信息的传递过程中，被加入噪声也是一种普遍现象，而对于图像传递而言常见的噪声有椒盐噪声和高斯噪声等。

该算法针对这两种噪声攻击进行仿真实验，证明了算法可以抵御噪声攻击，实验结果如图8、图9所示，两幅图的第一行显示的是分别对加密图像加入椒盐噪声和高斯噪声的图像，第二行是从干扰后的图像载体中恢复出来的图像，重建图像虽然能够看出噪声干扰但是仍然能够识别出原始图像主要信息，恢复结果比较理想。

4、滤波攻击

滤波处理常作为用于信号平滑处理，在图像信息的传递中也成为普遍的干扰攻击。该实验以常见的高斯低通滤波为例，利用大小为3*3模板的高斯低通滤波对加密图像进行攻击操作。实验结果如图10所示，第一行是经过高斯低通滤波的加密图像，第二行为通过解密算法后相应的重建图像，从恢复图像的效果上可见，重建图像受到了部分干扰，但原始图像的主要信息仍可辨认，恢复效果很好，说明该算法可以抵御此种攻击。

五、安全性及时间分析

1、密钥空间分析

本文所提出的加密算法中，密钥有两部分构成，一部分是对于Logistic数列形成的初值ro和参数阳的选取，另一部分密钥则是混沌序列Hybrid的初值及其它参数的选取。取值符合范围即可，由此可见两种密钥的组合数量能够抗击穷举攻击，因此，该算法在应用领域具有很高的安全性。

2、时间分析

算法的运行时间是运行成本的重要指标，该加密算法运行时间短，能够达到应用要求。如表1所示，是在如下配置的机器所完成的时间计算：windows 7，Intel (R) core(TM)2 Duo CPU T5750@2.OOGHz，内存2GB。该表反应了对于不同图像的加密解密时间，从表中可以看出该算法运行效率很高，极大的减低了运行成本，更能适应正常应用对算法时间的要求。

admin普通用户

海报分享