基于跳跃轨道的数字序列混沌加密算法

任何非线性系统的混沌状态都是由无限不稳定的周期轨道组成。对于任意给定的初始状态值，混沌系统不能自发地移动到任何一个轨道上。即该混沌系统可以不受任何外界影响落到这些轨道上的几率接近零。但是，一旦混沌系统运行于这些轨道上，就不会脱离这些轨道除非对其进行外加控制。由于混沌系统的普遍性和其对初始状态极强的敏感性，可以通过改变系统参数，改变系统演化轨道，使混沌系统从一个周期轨道转换到另一周期轨道。但是对于一个普通的非线性系统（非混沌），要达到同样的效果非常困难。混沌系统的该特性提高了数字序列加密方法的安全性。

本文提出一种新的数字加密算法，该算法将加密序列映射至几个不用的混沌周期轨道，然后将通过另一个非线性系统迭代周期轨道系统的参数得到的短序列作为重构这些周期轨道的密钥。在解密端，采用基于改进的Newton-Raphson算法的混沌轨道阴影法获取这些系统参数。该加密算法中的密钥不仅包括混沌周期轨道的初始条件值，同时也包括非线性系统的模型参数。该加密算法的特殊性使加密序列可以完全随机，而且该加密序列不带有原序列的任何信息。因此对于攻击者来说，从参数空间估算模型参数是非常困难的；其次，只有获得周期轨道的确切初始值，才有可能解密。但是，因为混沌系统的演化值对于初始条件具有极强的敏感性，获取周期轨道的精确初始值几乎是不可能的。相对于其他加密算法，本文加密算法除了具有较强的抗破译性，也不需要任何空间坐标对的转换。而且，由于Newton-Raphson的快速收敛性，粗略的初始条件估计值是可以达到理想效果的，重构周期轨道的参数演化序列也会非常短。因此该算法在应用中更容易实现。

一、一种新的数字加密算法

1、杜芬振荡器的周期轨道

杜芬振荡器是一种被广泛研究的特殊非线性系统。标准表达式如式(1)所示。

在式(1)中，如果δ值已经确定，当δ值由小到大变化时，系统状态也相应由小周期行为转换为混沌行为，并且最终达到极大周期行为瞪阄。因为基准信号γcos(t)的频率是连续的(1 rad/s)，杜芬方程的使用因此被限制在一个有限的定义域中。于是，ω0=2πfo，式(1)可由式(2)表示如下。

式(2)中，令fo=0.2Hz，δ=0.3，使用四阶龙格库塔算法可以分别得到δ=0.2和δ=1.5时(x VS y)的平面图。为了方便比较，将两图显示在同一图中，如图1所示。

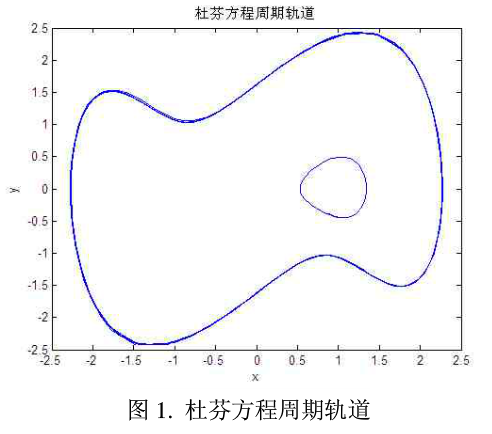
当δ= 3.5时，杜芬振荡器处于混沌状态，下图2是其吸引子。

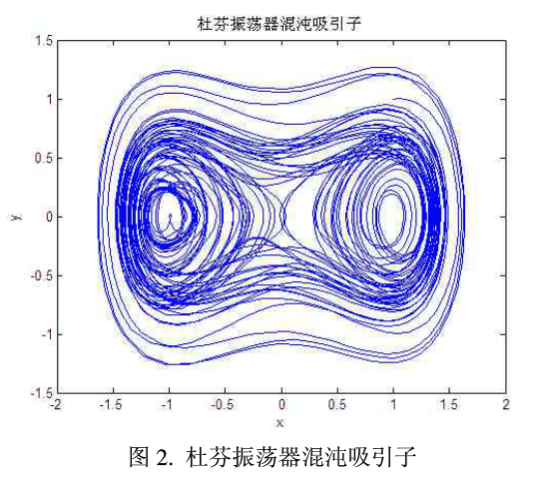
当δ= 0.3（或者其他值）时，γ的值不同系统显示出不同状态。当γ∈[0.05，0.26]，系统表现为小周期行为，当γ∈[0.27，0.43]时，系统为混沌状态，但是当γ∈[0.44，10.32]时，系统状态表现为极大周期行为。由此，可以得到另一个重要结论，小周期轨道与极大周期轨道是分离的。即这两个轨道之间没有任何交叉点，这对于数字序列加密方法至关重要。而且，所有周期轨道的形状完全不相同。

由混沌的可定义性可知，如果／取值属于小周期轨道或者极大周期轨道的参数值域，系统轨道必定会演化并最终落在相应的周期轨道上。同时，由于混沌系统固有的随机性，轨道上每一点的坐标都是随机的。在两个周期轨道参数域间转换／的值促使周期轨道转换，这种现象被称为“周期轨道跳跃”。

2、数字加密算法

对于一个给定的δ值，与其对应的γ的小周期轨道取值域定义为A，极大周期轨道取值域为B。假设数字序列如式(3)所示。

其中，ai∈{o，1}{i=1，2...n）。在该加密算法中，式(2)的初始条件是关键，该初始条件必须使求得的解在该方程的周期轨道上。对于随机给定的初始条件(x0，yo)，不需要马上就落到一个周期轨道上。但是，当γs∈A时，可由式(2)演化的上一步的结果值得到点（Xsi，ysi）。同理，当γg∈B时，迭代式(2)可得到点（Xgi，Ygi）。此时（xsi，ysi）和（Xgi，ygi）都位于各自的轨道上，并且都是初始条件相对应的轨道周期。

当ao取值O时，令γ=γs，式(2)由初始条件(Xsi，ysi)演化一步。那么ao被映射为小周期轨道上的一个点。相反，如果ao取值1，令7=yg，那么ao将映射到初始条件为(Xgi，Ygi)的极大周期轨道上的某个点。不论点在哪个轨道上，初始点都为(x0，Yo)。同理，ai被映射到点(xi，yi)。当映射呸时，其初始条件一定是(Xi-l，Yi-1)。否则，式(3)中的相同坐标对映射的点对也会相同，那么加密序列会很容易被解密。

式(3)的序列被映射为一个新的序列，如式(4)所示。

在该式中，每个坐标对都是随机的并且对于一段不是很长的序列来说是唯一的。将序列映射到几个混沌轨道，但是需要首先得到坐标对，然后将序列映射两次以达到算法的性能。除了初始条件(Xsi，ysi)和(Xgi，Ygi)，参数δ，γs，γg对于加密和解密也至关重要。因此，本文中通过一个非线性系统将其转换为一个短序列，进一步加强安全性能。该短序列和式(4)中的加密序列共同组成最终的加密序列。解密时，如果非线性系统的模型参数已知，δ，γs，γg可由短序列获得，重建周期轨道。那么通过判定每个坐标对坐落的轨道，就可以解密得到原始序列。

二、关键参数的转换与计算

1、转换序列

已知Rossler系统方程如式(5)所示如下：

当模型参数为a=0.2，b=0.2，c=9.0，该系统为混沌系统。其吸引子如图3所示。模型参数也可为任意其他使其呈现混沌状态的值。

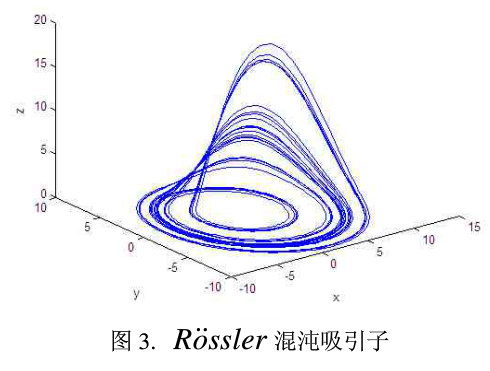
将δ，γs，γg分别赋值为其参数值域中的某个值作为式(5)的初始条件。迭代式(5)，由状态变量xl，X2，X3可得到3个随机向量。由于该系统状态变量之间互相影响，任意一个状态变量的演化向量必然包含完整的系统信息。那么，可从每个向量中截取一个短序列作为参数δ，γs，γg的转换序列，这些序列对部分状态变量可见的系统是非常重要且必须的。

现在，必须有一个算法可以由这些短序列准确估算出式(5)的初始条件，即δ，γs，γg。

2、初始条件估测算法

随机从式(5)吸引子中选取(Xli，X2i，x3i)赋值给δ，γs，γg。其中，(Xli，X2i，X3i)的值必须分别落入δ，γs，γg的定义域内。将这些数据作为式(5)的初始数据。将Eq(5)改写为三维自治混沌系统的矩阵形式，如式(6)所示。

x= (xl，X2，X3)T∈Rn为状态向量。假设方程向量已知为F=(FI，F2，F3)T，初始状态向量z(O)=（δ，γs，γg）丁，时间演化的状态向量x(t)可以唯一确定。目标是估算x(0)的值。

从短序列截取一个状态变量的值(Xli，X2i，X3i)。不失一般性情况下，选择状态变量x1)。

令y(o)指代x(0)的初始猜测值，从式(6)获取时间演化值y(t)。令e(t)指代误差可得式(7)，如下所示：

y(o)由x(l)演化得到且满足e(t)=0。由混沌系统的时间演化序列由初始条件y(o)唯一确定的属性可知，y(o)等价于x(0)。该方法是一种改进的Newton-Raphson方法。

引入xn= x(nΔt)指代第N个样本，Δt代表步长。同理yn= y(nΔt)且：

令Δy0= x0-yo=e0那么，可得式(8)，如下所示。

最后一步为AΔ0的泰勒公式的扩展式。对于At值较小时可写为式(9)，如下所示。

将式(9)带入式(8)忽略高阶部分得到式(10a)，如式(10a)所示。

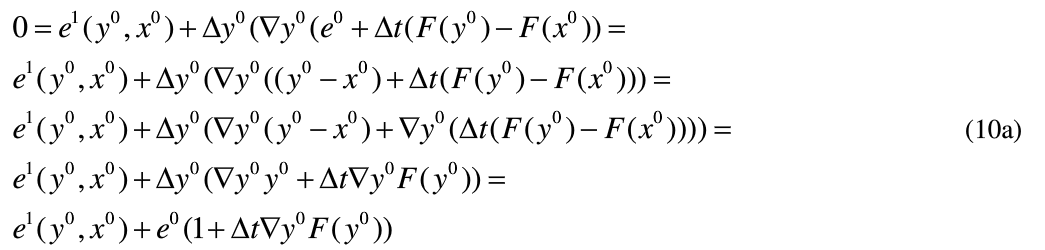
式(10a)的等价式可表示为式(10b)，如下所示。

式(10b)的矩阵形式如式(11)所示。

E1是向量81相应的列矩阵，I为单位矩阵，其元素可由式(12)得到。

同理，e2或E2可表示为式(13)，如下所示。

由式(6)迭代n步得到矩阵误差如式(14)所示。

令y10=x10，可由X1的序列得出x0=(x1(o)，x2(o)，x3(O))，其中Y2，Y3可以是任意猜测值。那么，y(t)的初始猜测向量为yo=（x0，rand, rand）。

这里e10=y10一x10，即△y10 =Oo由式(12-14)演化得到丽个方程用于计算△y20，△y30，如式(15)所示。

其中，E20和E30分别指代△y20，△y30，d为系统维数，这里为3。

因此，初始猜测向量可以通过一步演化改进，如式(16)所示。

给出初始向量yo经过几次迭代过程yo会收敛至xo=δ，γs，γg。由式(15)可知，x1只有两个样本值，xl和砰已知并且用于整个过程。得到加密序列如式(17)所示。

(x10,x11,x12)是x1的由方程(6)以δ，γs，γg为初始条件迭代后的前三个样本值。

三、加密实例

1、加密

假设Rossler系统第n次迭代的状态向量数据如式(18)所示。

使用上面的数据作为初始条件，可得到X1的演化序列。最初得到的序列可由式(19)表示。

由式(18)可知，这三个元素中没有任何一个值落在δ，γs，γg的参数值域中。事实上，由于数据是随机选取的，要使三个元素值分别落在相应的参数值域中是非常困难且不必要的。可通过式(20)的简单转换得到所需的值。

通过相似转换可以落入δ，γs，γg参数值域的数据并不唯一，其转换方式也不唯一。

令杜芬系统的小周期轨道的初始条件为γs=0.2，xs (0) =12013，γg(0)=-0.0849，对应的极大周期轨道为γg=1.5，xg (O)=2.032 6，yg(O)=-0.8931。初始值也可以是其它任意落在相应轨道上的值。为了说明简便，加密一个8位的数字序列，如式(21)所示。

值为“1”时，将其映射至极大周期轨道；反之，值为“0”时，映射至小周期轨道。加密后的序列为：

为获取δ，γs，γg的值，必须在解密端提供x的短序列值。因此，最终得到加密序列如式(23)所示。

该加密序列中，不仅数据由不同系统和不同的周期轨道获得，而且每个周期轨道上的坐标值都是完全随机的。

2、解密

首先计算当a=0.2，b=0.2，c=9.0时，式(5)的参数δ，γs，γg的值。式(23)中code_kpara部分为Rossler系统的状态变量xl的样本序列。假设δ，γs，γg原始猜测值如式(24)所示。

代入式(16)，得到迭代结果如下图：

分析表1可知，y0快速且稳定的收敛。将最后得到的值代入式(20)得到式(25)。

通过确定式(23)中每对坐标数据所在的轨道，可解密得到原始数字数列。解密序列01101010，为原始序列。实验表明，即使周期轨道初始条件的估测误差为10-16，解密也会失败。例如，当ys (O)=-0.893 100 000 000 000 1，解密序列将会是00001010。同理，周期轨道的参数误差为10-14，解密也将失败。例如，当ys=1500 000 000 000 01，因为a，b，c的估测值都是错的，解密后的序列为0000。

admin普通用户

海报分享