基于位平面变换的数字图像加密算法

已有数字图像加密算法存在算法运行时间成本高及加密图像抗攻击性弱等问题。为此，提出一种基于位平面变换的数字图像加密算法。该算法将图像分解为若干位平面，通过定义一种混沌序列的新变换对图像位平面进行换位加密，从而置乱像素点位置，在位平面间增加密钥进行乱序处理实现阿像像素点灰度值的变化。

一、位平面分解及序列变换

1、二进制位平面分解

由于数字图像每一个像素点的灰度值均可以表示成二进制数，这样从二进制每一位的微观角度出发，能够将图片分解为若干个位平面。如图1所示为利用二进制分解法将图像分解为8个位平面。从图1中可以看出，图像的重要信息主要包含在高位位平面中，从低位位平面的显示效果中不可识别原始图像信息，因此，利用此位平面的分解特点可以实现局部的图像加密。

2、序列变换

混沌运动由于具有非周期且不收敛、运动轨迹中的点能够遍历整个区域以及对初始值极为敏感等特征，因此，可以产生数量众多、非相关而又确定可再生的混沌序列。此类序列常用于对数字图像进行混乱加密，本文利用的Logistic映射就是一种被广泛应用的混沌系统映射，其定义模型如式(1)所示：

其中，O<μ0≤4；O<xo<1；n∈N，μ0又叫做分岔参数；Xn在区间[0，1]上遍历。

由于数字图像可以被看做一个二维矩阵，因此本文将提出一种新变换，该变换能够将所得的混沌数列转换成二维矩阵，从而实现对二维图像像素点的位置混乱。如要对mxn的二维数字图像进行混乱加密时，分别需要对其每一行和每一列进行位置置换，矩阵转换法则如式(2)、式(3)所示，设Cr和Cc是所需要的行列变换矩阵：

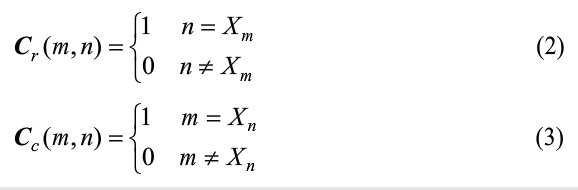
其中，m和n为所形成行列变换的位置下标。

如若要对8x12的图像构造置换行列矩阵，求得结果如图2和图3所示，此变换应用的数列是由初值x0为4、μ0为0.68的logistic映射所生成的，利用式(2)、式(3)产生大小对应的8x8的行矩阵和12x12的列矩阵。

二、加密算法

该算法的加密步骤如下：

(1)对图像含有重要信息的高位平面进行像素位置置换加密。在该步骤中，本文实验选择对图像第7位和第8位进行加密。设原始图像4尺寸为mxn，行列变换矩阵为Cr和Cc，则Cr和Cc的大小分别为mxm和nxn，四代表此步骤加密后的图像，Et代表原始图像中需要加密的位平面构成的矩阵，位置置换加密如式(4)所示：

这样，所得的二维矩阵E即为加密完成的位平面。

(2)有位平面乱序处理，从而实现整体图像灰度值统计的变化。由于本文实验的位平面分解采用二进制分解，因此进行乱序的密钥需要一个8个元素的置换映射，该密钥的增加扩大了该算法的密钥空间，增加了算法的安全性。

此算法的解密是上述方法的逆运算，分为2步：

1）将加密图像的位平面恢复到原始顺序；

2）根据行列式的性质特征以及矩阵乘法之间存在可逆性。

通过式(5)对第7位和第8位位平面进行解密处理，矩阵Et'中各元素的位置即为原始位平面元素位置。

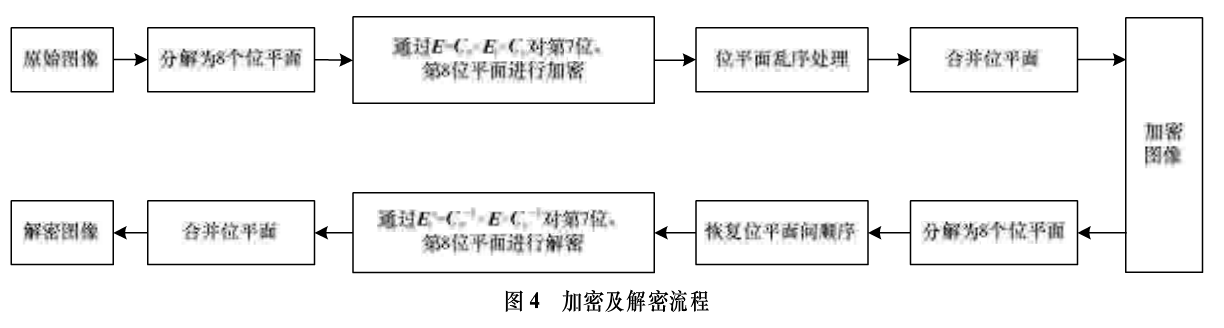
最后合并所有位平面即可得到解密图像，算法的加密及解密流程如图4所示。

三、仿真实验结果

1、实验结果

为了验证算法的可行性，应用Matlab软件作为开发工具，通过编程实现基于位平面变换的数字图像加密算法。本文分别针对不同形状的图像进行实验，如图5、图6分别列出对256x256像素的Lenna图像及255x181像素的长方形Lenna图像所进行的加解密算法实验结果。本文实验在步骤1中，分别自定义μ0和x来生成logistic混沌序列，并根据式(2)~式(4)将序列转换成相应的行列矩阵进行加密。在图5、图6中，(a)表示原始图像，(b)表示加密后的图像，(c)表示解密图像，从所给的实验结果可以看出，此算法对于不同尺寸的图像均适用，并且加密效果良好，不能从加密图像中辨识出原始图像。从(c)图解密图像可以看出，该算法的逆运算能够将原始图像成功还原，解密图像可辨识。另外，本文引入了SSIM标准，它是一种衡量2幅图像相似度的新指标，该标准常用于衡量原始图像和解密图像之间 的相似度，其值越大越好，当测得值为1时说明2幅图像相同。

2、安全性及时间分析

（1）切割攻击

图像信息在传递的过程中，当受到切割攻击后，恢复的图像由于缺失原始图像部分信息往往不能被识别，下文进行的实验就是对所得到加密后的图像进行切割处理，然后再从受到破坏的图像中恢复出原始图像，如图7所示，图7(a)、图7(b)、图7(e)、图7(f)为分别对两幅加密图像的边缘和中部进行切割的效果图，图7(c)、图7(d)、图7(g)、图7(h)显示的是对破坏后的图像进行恢复所得图像，从图7中可以看出，虽然恢复的图像有一些瑕疵，但是仍然可以清楚地辨析出原始图像的主要内容。

（2）噪声攻击

在数字图像加密中，图像在传播过程中最容易受到的干扰就是被加入噪声，噪声是一种典型的无意攻击，它会对加密图像产生影响从而导致图像质量下降。本文实验以常见的椒盐噪声为例，实验结果如图8所示，图8(a)～图8(c)是对256x256像素的图像进行加入椒盐噪声处理及恢复；图8(d)~图8(f)是对255x181像素的图像进行加入噪声处理及恢复。从实验结果可以看出，虽然图像有不同程度的干扰，但仍然可以看出原始图像的重要信息。

（3）滤波攻击

图像在传递过程中也容易受到滤波器影响导致图像降质，本文所用的是最常见的3x3模板的高斯低通滤波攻击，高斯低通滤波实际上是一种信号的滤波器，共用途是信号的平滑处理。如图9即为对高斯低通滤波处理后的图像及其恢复情况，图9(a)～图9(c)是对256x256像素的图像进行滤波处理及恢复；图9(d)~图9(f)是对255x181像素的图像进行滤波处理及恢复。可见，恢复的图像完全可以辨识原始图像的信息特点，此算法可以适应滤波器的攻击。

（4）统计分析

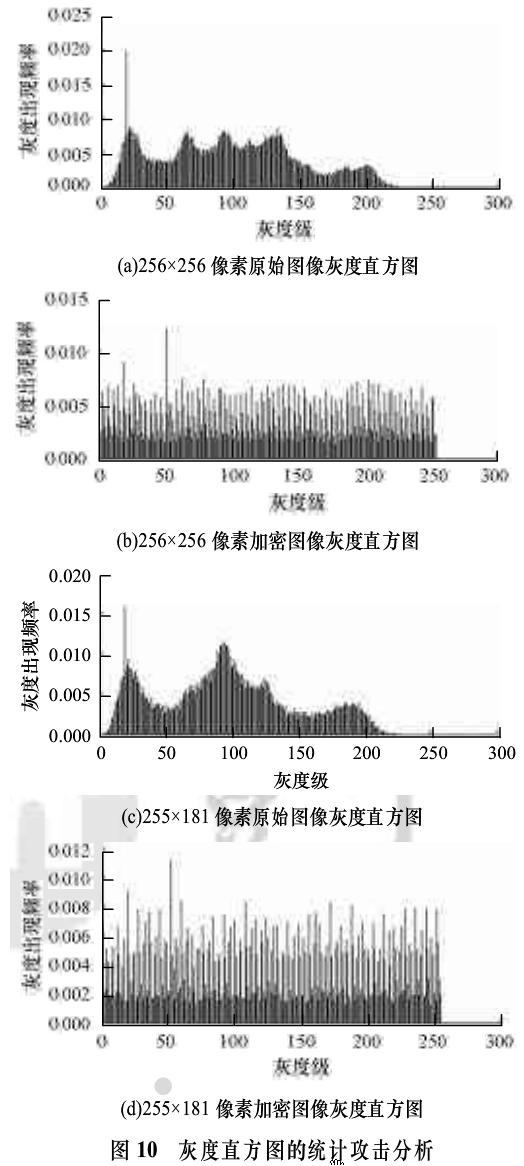
抗统计分析攻击能力的强弱也是评判图像加密算法优劣的重要标准之一，上文提到的对于图像位平面排列顺序置乱目的是为了防止进行灰度统计攻击，实验结果如图10所示，该算法的加密图像与原始图像的灰度值统计分布发生了明显变化，图10中显示运用此算法后，图像的灰度分布均匀，从而使得处理后的图像能够抵御灰度统计攻击。

（5）密钥空间及相关性分析

该算法的密钥空间很大，大体分为加密位平面的选取、对位平面加密的方法以及置乱位平面顺序的置换映射三部分。就本文算法而言，第一部分选取位平面的密钥量为C82；加密位平面密钥取决于μ0和x的选择，2个参数只要取要求范围内的实数即可密钥量极大；最后置乱置乱部分，本文的密钥量为A88的全排列。由此可见，该算法大范围扩展了密钥空间，使得攻击者不可通过枚举等方法对加密图像进行破译。

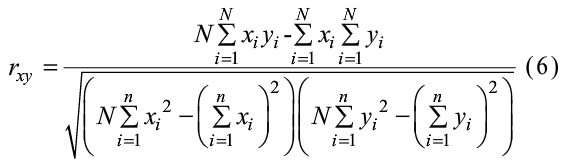
为进一步证明该算法具有很强的抗攻击性，相关性分析也是一个重要衡量指标。相关性分析是指对2个或多个具备相关性的变量元素进行分析，从而衡量2个变量因素的相关密切程度，对于数字图像的像素点来说即是对2个水平的、垂直的和对角邻近的像素点的强度变化进行分析。式(6)是相关系数的计算方法，x,y是2个相邻像素的强度值，N是像素点总数。相关性系数的值在-1和1之间变化，Yxy接近1说明相邻2点具有很强的相关性，而接近0意味着2个相邻点具有非线性关系。从表1中的第1列和第2列列出的加密前后相关性系数可以得出加密后的图像相邻像素点具有非线性关系。

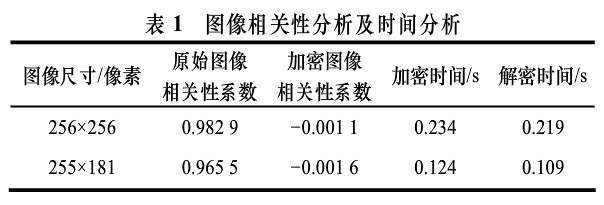
算法的运行时间能够反映出加密算法的效率，反映设计特点是否能够符合对应用时间的要求，表1的第3列和第4列显示的是该算法对于不同图像的加解密运算时间。表格给出的运行时间应用在Window7的系统上，采用较低的电脑配置如下：InteI(R) core(TM)2 Duo CPU T5750@2.00 GH，内存为2 GB。从表1的内容可知，对于普通的图像来说，此算法加密时间快、运行效率高，能够满足正常操作的需要。

admin普通用户

海报分享