时域图像加密算法
在象因特网这样的开放网络中,数据加密被广泛使用以保证信息的安全性。每一类数据都有其固有的特点。因此,应该使用不同的加密技术保护保密数据防止非授权使用。对于文本数据,有许多可以使用的加密算法。然而,适用文本数据的算法不一定适用于图像数据。图像有其固有的特点如:
(1)数据量大;
(2)邻域像素间具有很强的相关性,任何指定像素值能合理的从邻域像素值中推测等。
目前,根据图像自身特点,有许多加密算法被提出。从变换域角度来看分为时域加密和频域加密。本文主要研究高度保真图像,如医疗图像等,对于图像变换到频域进行一定处理再反变换到时域这种变换域的加密方法使图像存在一定的损失,因为病变部位突变较大,频率较高,频域变换会使一部分高频分量丢失,当解密时,解密图片将存在一定的失真,导致失去原有图像的含义。故本文加密方法只研究时域算法,满足高保真图像的需求。
一、相关时域图像加密系统
目前,时域加密比较先进的是非线性的混沌加密,该算法使用正规语言产生扫描模式,并且通过对二维存储空间的不同访问方式来产生非常大的扫描路径曲线。通过对扫描模式的像素位置改变和灰度值的替代相结合,共同完成图像加密算法。如应用复合混沌系统即对图像像素位置进行置乱又对图像像素值进行扰乱的图像加密系统。如一种新的基于超混沌序列的数字图像加密算法。首先应用Hyperhcnon映射产生混沌序列,用此混沌序列对图像做预处理加密,接着应用Kawakami映射产生混沌序列,对预处理后图像的行和列分别做改进的魔方置乱。属于先加密后置乱。如基于密文和输出混合反馈的混沌图像加密算法。利用密文扰动混沌系统的初始值。这种加密算法属于单一图像加密,但每次都改变混沌初始值。另外,还有大量的文献给出了时域的图像加密算法。通过总结这些文献可以得出,时域混沌加密主要有三种形式,单一置乱像素位置,单一改变像素值,以及混和加密。
如目前已经证明单一置乱加密方式可以破解,而单一变换像素值加密没能消除图像固有的相关性。故本文提出时域内分块置乱和具有后效性的混沌混合图像加密方式。
二、全新混合时域混沌加密系统
1、基于混沌理论的图像分块重排算法
图像是由基本单元像素组成,像素在图像空间按某种规律排列,相互之间有一定联系。常用的像素邻域有3种:4邻域、对角邻域、8邻域。
根据像素邻域的三种关系,可分别测试两个水平相邻像素的相关性,两个垂直相邻像素的相关性,两个对角相邻像素的相关性。
相邻像素的相关性算法:以水平相关性为例,从图像中随机选择1000对两个水平邻接像素,运用下面公式计算每一对相邻像素的相关系数。
![]()
x,y图像中两个邻接像素灰度值,在数值计算中下面的离散公式被使用:

以大小为256x256的8位灰度Lenna图像为例见图1。

其水平(垂直,对角)相邻像素的相关性见表l第二列。统计数据表明,原始Lenna图像相关性很强,这意味着很容易从相邻像素推出任一给定像素。为消除相关性,根据香农扩散理论,我们提出了如下置乱算法。
(1)载入明文图像;
(2)获得明文图像的长度和高度;
(3)输入混沌密钥和分块大小,产生分块图像置乱顺序索引;
(4)获得分块之后的水平块数和垂直块数,计算总块数;
(5)基于混沌置乱序,重排分块图像;
(6)结束重排图像。
以大小为256x256的8位灰度Lenna图像为例见图1,图2为把原始图像划分成每块2×2的分块图像,然后经过混沌置乱后的结果。置乱后其水平(垂直,对角)相邻像素的相关性见表1第三列。图3为把原始图像划分成为每块8×8的分块图像,然后经过混沌置乱后的结果。置乱后其水平(垂直,对角)相邻像素的相关性见表1第四列。

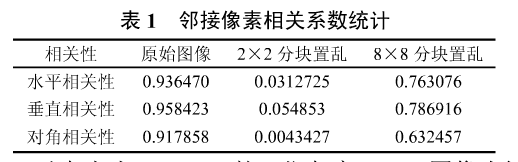
统计数据表明,通过重排极大地减少了像素之间的相关性。分块越小,相关性越弱。图像2x2分块置乱运行时间为0.06s,8x8分块置乱运行时间为0.04s,从运行效率来看,完全符合实际需要,可以很好地在工程中使用。但是目前已经给出证明,单一混沌置乱是可破解的。并且指出,为增强安全性,置乱之后必须进行混沌加密操作。
2、具有后效性的混沌加密算法
(1)加密算法
1)打开一个文件并过滤头信息;
2)从文件中以字节为单位读图片数据及I(k);
3)根据选择的混沌方程(如logistic方程),依据密钥生成混沌序列陇),并量化获得一个比特,循环8次,组合为一个字节φ(k);
4)根据如下公式进行加密计算:
![]()
获得密文字节e,k={1,2,…};
(5)将g写到一个新文件中;
(6)重复(2)到(5)直到文件结束。
说明:φ(k)混沌方程产生量化组合的字节,I(k)图片的一个字节,C(k)当前字节的密文。其中C(O)为随机种子,为密钥的一部分。N图像色彩的级数,本文为灰度图像256级。
混沌后效性的体现在第(4)步的加密公式中:当前字节I(k)的密文形成不仅与当前φ(k)混沌密钥相关,而且还与前一字节的密文紧密联系。这样攻击者很难破译。
(2)解密算法
第(4)步根据如下公式进行解密计算:
![]()
其他步骤同加密算法。
以大小为256x256的8位灰度Lenna图像图1为例,其中图4为仅仅使用具有后效性的混沌加密算法得到的图像。图5为图像2x2分块后混沌置乱并且采用具有后效性加密算法的图像加密结果,即
混合加密结果。其中图6为图像8×8分块混沌置乱混合加密结果。

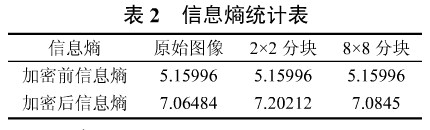
从表2信息熵统计表可以看出,图像经过混合加密后,信息熵显著提高,分块越小,信息熵略有提高但不显著。
三、安全性分析
加密图像的安全性是一个重要问题,下面将从统计攻击和差分攻击两方面来分析本文提出的加密算法抗击外界攻击能力。
1、统计分析
统计分析包括直方图分析和相邻像素点的相关性分析。本文采用相邻像素点的相关性分析检测算法抗统计攻击能力。
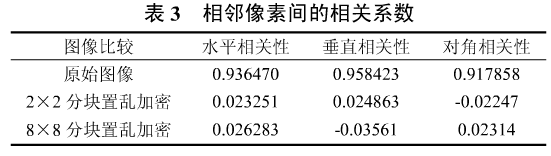
原始图像和加密图像相关性分析见表3,由表可知,原始图像相邻像素相关系数接近1,加密图像相邻像素相关系数接近0。经加密,图像相邻像素间相关度很低。说明攻击者很难通过统计攻击方法解析加密图像。
2、差分分析
差分分析指攻击者将获取的已加密图像任意改变一个像素值,得到一幅新的图像,然后对该图像进行加密,观察变换结果。通过这种方式,有可能找到明文和密文有意义的关系,如果已加密图像微小变化能造成密文巨大变化,则差分攻击无效并且无实际意义。
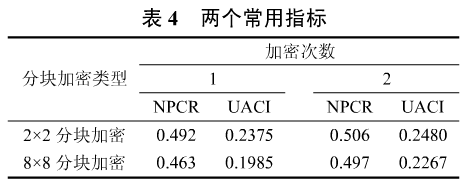
像素个数变化率(NPCR)和整体平均变化密度(UACD是衡量抗击差分攻击的两大指标。前者描述两幅加密图像对应位置像素值不同的个数比率,后者描述不同像素值差异程度。计算结果如表4。
表4说明随着加密次数的增加,NPCR和UACI的值呈上升趋势。因而,加密算法能有效抗击外界差分攻击。
通过对比不同分块大小的相关性得出,分块越小,相关性越低。但分块大小对信息熵的提高并不显著。应用者可从实际出发选择合适分块大小的混沌置乱算法。
小知识之时域
域表示范围,时域是一个数学或物理词汇,表示以时间为轴线,以时间为标尺为基准。









