一种保持非负整数值的图像加密算法

近年来，互联网技术飞速发展，在网络上传送音频、视频和图像等多媒体信息的需求也日益增多，与此同时，人们对互联网信息传送过程中的安全性和保密性要求也越来越高．加密方法是对信息进行编码和解码的方法，对图像信息的加密方法可以分为三大类：

1)把图像当作普通的二进制文件来进行加密，这种加密方法可以使用包括DES、AES等传统的密码学算法来进行。但这种方法没有考虑到图像信息的特征，加密图像信息的微小失真会导致解密失败；

2)用图像处理技术的加密方法。其中又包括时域加密和频域加密2个子类：

①时域加密，典型方法是利用混沌系统来对图像进行像素置乱以及灰度置乱；

②频域加密，主要是采用分数阶傅里叶变换(Fractional Fourier Transform，FRFT)来对图像进行加密，因为FRFT的变换阶数可以作为图像加密的密钥，但该方法的加密结果是复数；

3)利用光学信息处理技术进行加密，指的是利用光学加密理论来进行数字图像加密处理。例如利用双随机相位的方法(Double Random Phase Encryption，DRPE)来加密图像，但该方法的加密结果也为复数，不利于图像的存储及传输，因而该加密方法主要在光学图像加密的计算机仿真时应用。

有不少学者研究如何建立一种实值图像加密方法，从而可以减少加密图像的信息熵，现阶段主要有三种实值加密方法：

1）将加密图像的存储空间扩大，但是需要存储及传输的数据量也对应增大，因此这种方法的效率不高；

2）利用希尔伯特变换，将图像压缩成二分之一的频域图像来进行处理，最后再把图像还原到实数域；

3）基于保持实值的分数阶傅里叶变换来进行图像加密，上述三种方法的加密结果都是在一个很大区间内分布的正数和负数的集合矩阵，不利于保存成数字图像。

本文提出了一种能够使双随机相位图像文件加密方法的密文图像保持为非负整数值的变换——重构变换。基于重构变换的双随机相位图像加密方法可以实现联合图像压缩和加密的效果。本文首先介绍图像重构变换的实现方法，并对其算法复杂度进行分析。之后，介绍重构变换在双随机相位图像文件加密方法中的应用，也即是实现了一种基于变换域的数字图像文件加密方法。最后，对保持非负整数值的双随机相位图像加密方法进行了实验分析，实验结果表明本文加密方法可以减少密文图像的信息熵和数据量并保持密文图像的安全性，且具有较大的密钥空间，密文
图像对于高斯噪音干扰和椒盐噪音干扰具有较强的鲁棒性。

一、重构变换

1、加密算法引入

重构变换包括预处理和频谱搬移两个过程，对于一幅具有256级灰度的图像，预处理的步骤可以记为以下两步：

Step1：设原图像h(x1，y1)的大小为M×N，将h(x1，y1)按上下对半的方式拆开为：

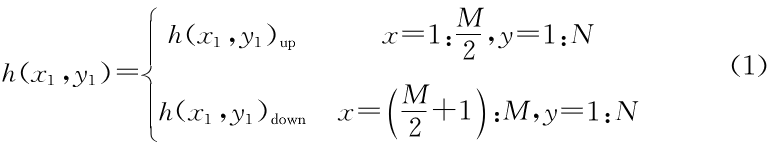
Step2：将h(x1，y1)。。当成图像的实部，h(x1，y1)down当成虚部，构造一幅M/2×N的复数图像，从而减少图像的运算空间。

式中k称为缩放因子，当k∈[3，4]时，解密的图像能够获得较高的恢复质量。缩放因子的作用是，减少密文图像的值域区间。

在经过预处理之后，复数图像H(x2，y2)可以进行传统的加密运算。为了使运算结果转化为256级灰度值，在复数域的加密运算之后需要进行频谱搬移，其步骤如下：

Step1：假设经过复数域处理之后的图像是大小为M/2×N的G(x2，y2)，分别提取其实部和虚部，即：

Step2：将图像拼接成为M×N的256级灰度图像h2(x1，y1)。

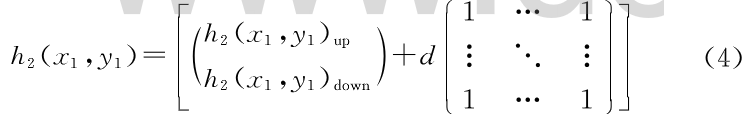
式中，[]表示取整，d称为搬移系数，当缩放因子是不同时，它会对应有不同的最优值。

图像重构变换的特点体现在以下几个方面：

1)通过叠加的方式将整数图像压缩成一半大小的复数图像，从而能缩小后续运算的计算空间；

2)缩放因子是的引入，使密文图像的值控制在[-128 128]之间，最后通过矗参量将密文图像值域移到[0 255]；

3)频谱搬移过程中，取整这一步骤会使重建的图像产生微小失真，但这些失真可以减少密文图像所需要保存的数据量，在加密的同时实现了压缩的效果；

4)缩放因子和搬移系数对应不同的图像会有不同的联合最优值，在实验分析中我们将对其进行探讨。

2、加密算法复杂度分析

在重构变换中，预处理需要进行M/2×N次的加法运算，频谱搬移需要（M/2×N+M×N）次的加法运算，因此重构变换的运算复杂度只有0(2M×N)，由上述分析可知本算法的运算复杂度很低。

二、数字图像的双随机相位加密方法

光学信息处理方法能够实现高速的并行处理、抗干扰能力强以及光速运算等优点．在光学图像加密方法中，双随机相位加密应用最为广泛，然而，该加密方法在数字图像加密中并不可行，因为它复数的加密结果包含了太多冗余信息．如果给合本文所提出的重构变换，那么光学加密理论中的双随机相位加密方法则能应用于数字图像文件加密。

光学图像的双随机相位加密过程如图1所示。

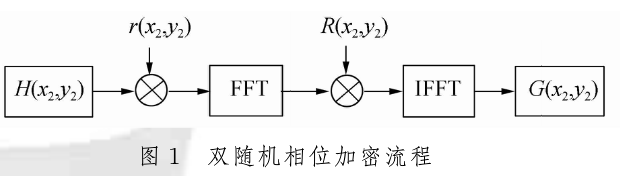
设原始图像为H(x2，y2)，r(x2，y2)，R(x2，y2)是随机相位掩膜，r(x2，y2)=exp (i2兀r0(x2，y2))，R(x2，y2)=exp(i2πRo(x2，y2))，r0(x2，y2)和R(x2，y2)都是取值范围在(0，1)的随机数。H(x2，y2)是加密之后的复数图像。

将重构变换应用到双随机相位加密方案中，则光学加密系统的加密流程如图2所示。其中加密步骤为：

Step1：对于一幅M×N灰度图像H(x1，y1)，通过图像重构变换中的预处理变换成等×N的复数图像H(X2，y2)。

Step2：用双随机相位方法将H(x2，y2)加密成G(X2，y2)，双随机相位加密后的图像G(X2，y2)可以表示为：

Step3：将图像G(X2，y2)通过频谱搬移转换成为M×N的H(x1，y1)，其中H(x1，y1)是在O至255之间的非负整数．因此，H(x1，y1)易于保存为数字图像并且在网络上传输非常方便。

解密步骤是加密步骤的逆过程，因为重构变换只是一些线性变换，所以本文所提出的保持非负整数双随机相位图像加密方案的光学实现在理论上也是可行的。

三、实验结果

为了验证重构变换算法的效率，我们在MATLAB7.O环境下使用Lena图像及hill图像，对基于重构变换的双随机相位图像加密方法进行分析，所使用图像灰度级别为256，大小是256×256。

1、加密图像的信息熵

为了衡量加密前后图像包含的信息量是否有变化，这里引入信息熵来进行度量．设图像矩阵的大小为M×N，矩阵的信息熵可写为：

式中0和255分别为该灰度图像像素的最大值和最小值，P(i)是数值为i的元素在矩阵中出现的概率。基于信息熵，传输数据的总比特数可以写为：

注意到式(7)对灰度图像的信息熵求解是针对整型值来说的，若图像是复数图像或非整型值图像，则需要通过分段统计的办法来计算信息熵，为了体现本文所提方案的特点，在表1中引入了其它典型的加密方案在密文图像的信息熵方面的表现性能，以进行比较。其中，双随机相位加密图像方法中保持密文实值的代表，利于混沌系统来对图像进行位置乱的加密方法，将图像的置乱和扩散操作联合起来的混沌加密方法。

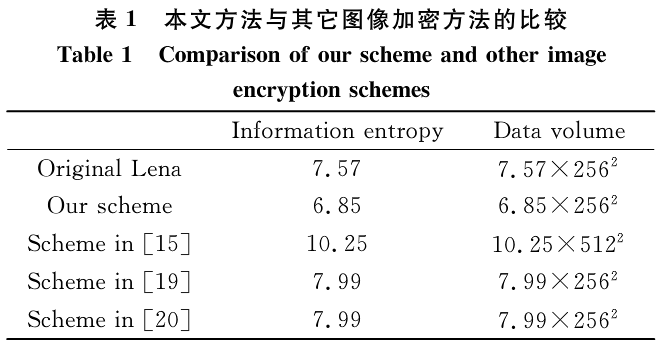
对于一幅具有256级灰度的整型值图像来说，其最大信息熵是log228=8。在表1中，这种0方法计算所得信息熵大于8，是因为其密文图像是非整数图像，信息熵计算采用2560个分段近似计算：统计像素值在每一段的出现频率，再计算其信息熵。又因其密文图像大小是原文的4倍，该方法需要传输的数据量非常大。

在表1中，后两种的方法都是利用混沌系统来加密图像的方法，这类方法能使密文图像具有趋于8的信息熵，但其劣势在于不易于图像压缩方法相结合。因为好的混沌加密方法都会具有较好的雪崩效应（一个原始图像像素位的改变会导致密文图像大部分像素位的改变）。由此，如果再将这些加密方法的密文图像进行有损压缩（比如变换编码，小波编码），则由压缩之后的图像无法恢复出原始图像。

本文方法的加密图像具有比原始图像更小的信息熵，实现了图像压缩与加密的联合。本文方法信息熵降低的原因是在进行重构变换的过程中，式(4)的取整运算丢弃了小数部分的信息，从图3(c)可以看到，本文方法的解密图像与原文图像的差别是人眼难以区分的。另外，从图3(d)可以看出，本文加密方法所减少的信息熵对应着解密图像的小部分轮廓信息丢失。

2、缩放因子k及搬移系数d的最优值

为了评估本方法恢复的图像质量，我们使用峰值信噪比(Peak Signal Noise Ratio，PSNR)，这一参量来进行测量。PSNR的定义式为：

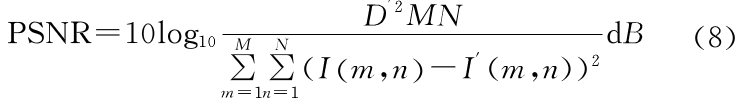
其中I（m，n）是原始图像的灰度值，I'（m，n）是恢复图像的灰度值，两幅图像的大小都为M×N，D'是图像灰度级别的最大值。

为了测量缩放因子k对加密效果的影响，我们先将搬移系数d固定为常量，将忍设置为在[2.55.5]内的自变量，对应的PSNR值为因变量，加密效果如图4所示。

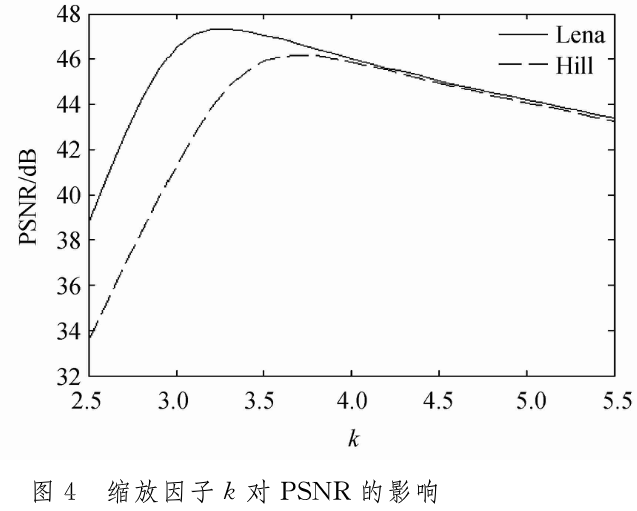
在图4当中，Lena图像对应的最优k值是3.2，hill图像对应的最优忍值是3.7。当是在[3 4]内取值时，恢复图像与原图像的峰值信噪比都大于40 dB，这时恢复图像与原图像的差别是人眼难以分别的，因而使用重构变换的方法来改良双随机相位加密具有实用性．如果将式(4)里面取整这一运算步骤去除，从加密结果就能够无失真地恢复原图，但是加密的非整数图像无法保存成位图文件，在另一方面，当缩放因子k越大，本文方案所加密图像的信息熵越小，其对原始图像的有损压缩率也就越高。

同理，为了测量搬移系数矗对加密效果的影响，我们可以将k固定为最优值区间内的3.5，然后以d在[113 143]区间内作为自变量，观察其加密所对应的PSNR值变化，变化效果如图5所示。

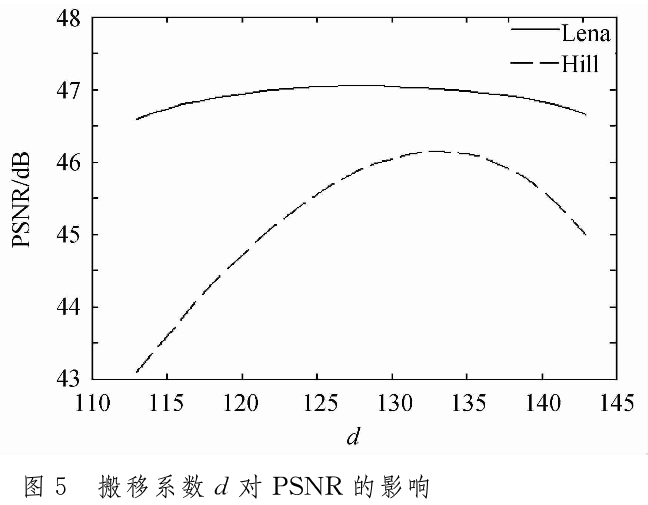
在图5中，当d取128时，Lena图像对应有最大的PSNR值，当d取134时，Hill图像对应有最大的PSNR值。从图5可以看出，Hill图像对搬移系数的变化较Lena图像敏感，原因是，式(4)的取整运算对于信息熵更小的图像影响更大。

对于一幅特定图像来说，如何求解k和d的联合最优值是一个求解二维多峰函数的全局最优值问题，可以采用群智能优化算法来进行快速求解（比如人工蜂群算法）。然而，如果在加密图像之前都采用优化算法来求出其联合最优值，则不能保证加密方案的实时性。由于当是在[3 4]内取值，d在[125135]内取值时，解密图像都能取得40 dB以上的峰值信噪比，因此，我们可以确立一个“联合最优区间”的概念，当忌和矗在联合最优区间内取值时(d∈[3，4]，d∈[125，135])，解密图像的微小失真是人眼不可见的。这种在联合最优区间内取值的方法可拟实现对不同图像的快速、高效加密。

为了对本方法的安全性进行验证，将缩放因子k和d移系数d在最优区间内分别取3.5和128，然后考察本文加密方法的密钥空间，以及对其进行统计分析。

（1）密钥空间分析

图像加密算法的密钥空间一般要足够大，从而能够抵抗穷举攻击。对于本文提出的加密算法，其密钥空间分析如下：随机相位板的每一个密钥位在MATLAB7.0上执行时都是双准确度实数，假设输入图像的大小为M×N，则本文方法对应的密钥空间为2×1015XMXN，假设尝试一次可能解所需的时间是1秒，则穷举一幅256×256密文图像所需要的时间特别长，可见该密钥空间是足够大的。

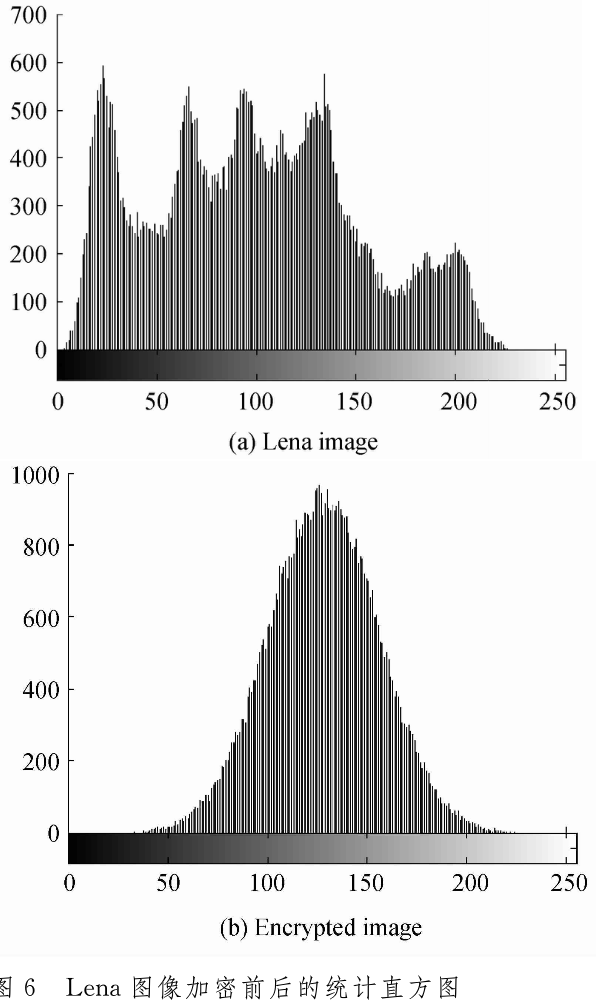
（2）柱状图分析

加密前后的柱状图如图6所示。从上图可以看出，加密之后图像的像素值近似于正态分布。本方法加密的任何图像都是这种近似正态的分布，因此这种分布的安全性不比均匀分布的安全性低。

（3）邻域像素相关性分析

分别从水平、垂直、对角三个方向来分析加密之后图像的相关性。为了提高计算效率，我们随机选取4000对像素点进行分析，其中计算像素相关性的公式为：

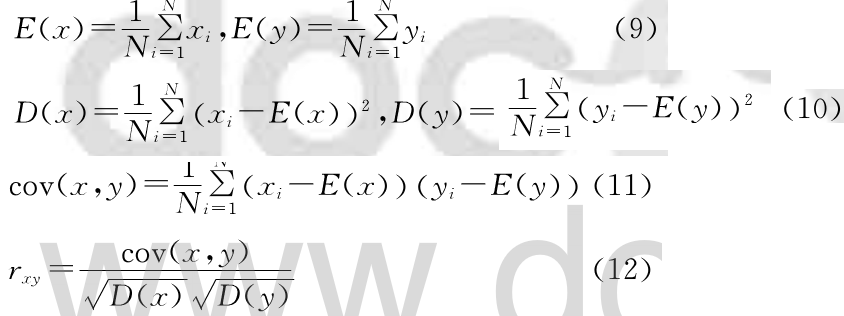
式中x和y分别表示图像中随机选出的像素对的两个灰度值，rxy为图像的像素相关性。从表2可以看到，原始Lena图像在3个方向的像素相关性都非常高，而加密之后的像素相关性都是负数，从而表明改进的双随机相位图像加密方案安全性高。图7为图像垂直方向的像素相关性。

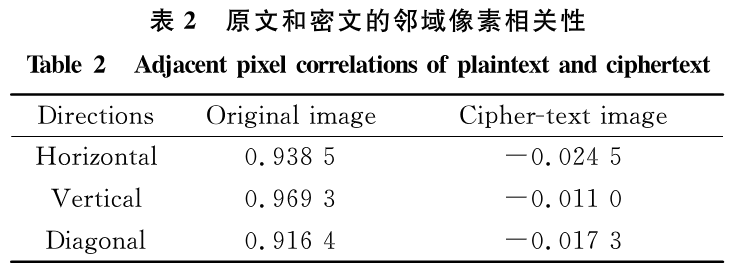
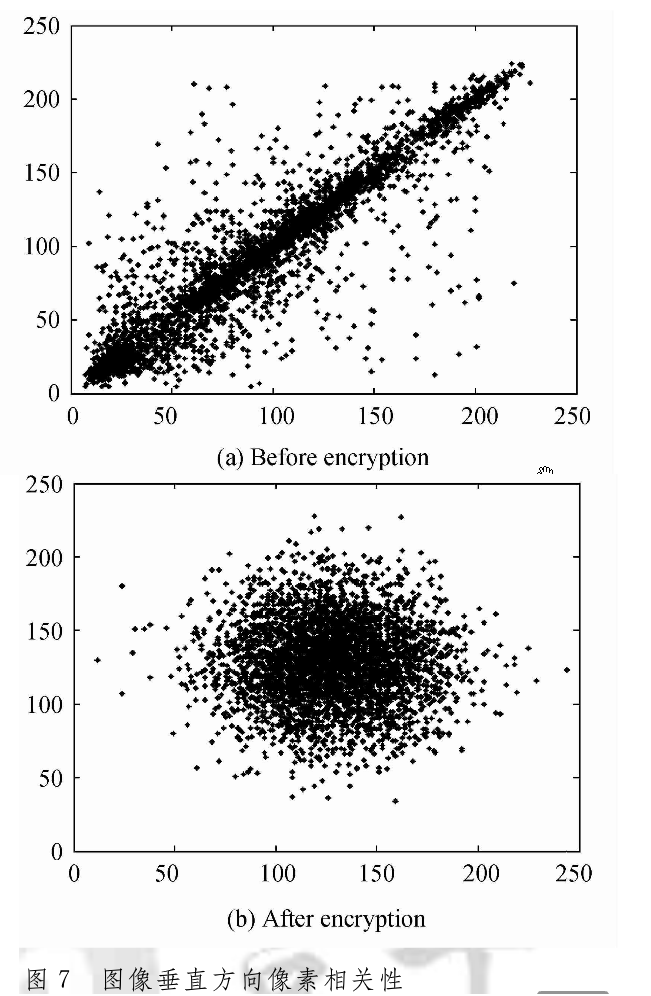
4、抗干扰性能

用图像处理的办法来加密图像的一个显著优点就是这种方法能抵抗一定的加性噪音干扰。对Lena图像应用本文方法进行加密，再对密文图像分别加上0. 001 dB的高斯噪音和0.001 dB的椒盐噪音，如图8(a)，(c)所示。对于被噪音污染之后的图像，它们解密后的图像分别如图8(b)，(d)所示，解密的图像基本都能分辨出人的轮廓和相貌特征。因此本文方法对高斯黪音及椒盐噪音干扰具有一定的抵抗能力。

admin普通用户

海报分享