admin 我们利用离散广义混沌同步定理，基于3D-Lorenz系统构造了一个新的离散混沌系统，并结合Arnold猫映射设计了一种音频复合加密方案。该方案首先用复合系统产生的混沌码对明文进行加密，然后将密文隐藏到wav语音信号中，解密过程能够实现无失真解密。
一、离散广义混沌同步系统
1、离散广义混沌同步理论
对两个离散混沌系统，有如下定义：
定义1 考虑两个混沌系统：
其中：
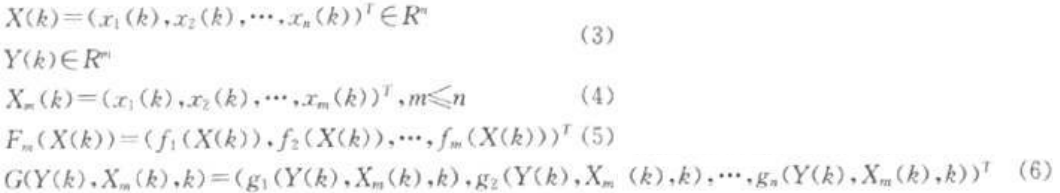
系统(1)称为驱动系统，系统(2)称为响应系统。若存在一个映射H：Rm→Rm和开集B=Bx×By⊂RmXRm，使得当初始条件(X(0)，y(O))∈B时，系统(1)和(2)的解(X(k)，y（k））满足：
则称响应系统(2)与驱动系统(1)关于H在B上离散广义混沌同步。若∀(X(O)，y(0))∈Rn×Rn，式(7)均成立，则称系统(1)与(2)关于H大范围离散广义混沌同步。
定理1 设X，Xm，y，F(X)及G(Y，X)由式(1)-式(6)定义，H:Rm—Rm是可逆变换，且xm=V(Y)=H-1(y)，假如式(1)与式(2)关于变换H是广义混沌同步，那么式(2)中的G(Y，X)可写成以下形式：
其中，
且函数，
使得误差方程：
零解渐近稳定。
2、离散广义混沌同步系统
复合加密方案首先需要构造一个新的离散广义混沌同步系统。基于3D-Lorenz方程并且形如式(2)的GCS系统具体描述如下：
设驱动系统X(k+l)=F（X（k））为3D-Lorenz方程：
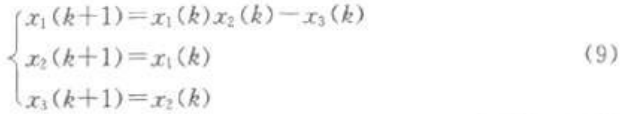
当x1(1)=0.5，X2(1)=0.5，X3(1)=-1时，系统(9)能够产生混沌轨道。，令H：R3→R3，构造一个可逆变换，形式如下：
式中：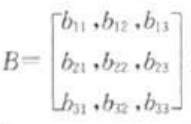
是一个3×3可逆矩阵，
再令m=3，
则，
使其零解渐近稳定，且q(Y，Xm)有形式：
由定理1得到响应系统方程；
另：
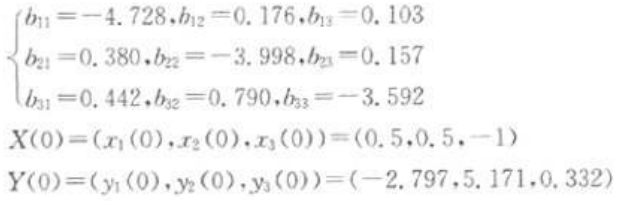
则系统(9)和系统(12)产生的混沌轨道如图1所示。从图1中可以看出，驱动系统和响应系统为两个混沌吸引子和关于传递函数离散广义混沌同步。
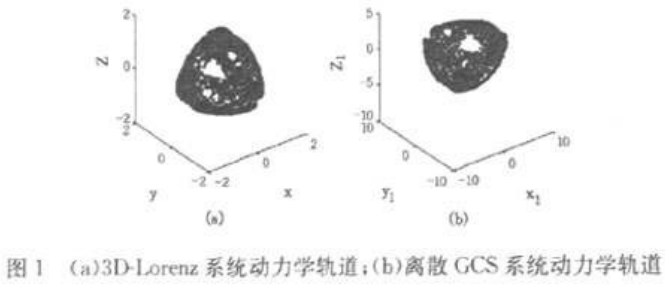
二、基于离散广义同步的复合混沌音频加密方案
1、Arnold离散猫映射
标准的Arnold离散猫映射属于=维混沌系统。Arnold离散猫映射的表达式如下：
式中，k=2。
当选择初始条件为X(o)一（0，1/根号2）T时，系统出现混沌现象。图2所示为Arnold离散猫映射取上述初始条件时前4000次迭代产生的运动轨迹。从图2中可以看出，Arnold离散猫映射的迭代点分布非常均匀。
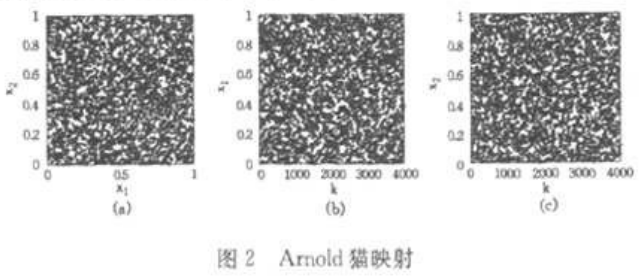
2、复合音频隐藏算法
本文基于离散广义混沌同步的3D-Loren2系统(12)和Arnold猫映射提出了一种复合音频加密算法。
假设发送方A需要通过传输网络向接收方B秘密发送一段txt文本信息撒，其隐藏流程图如图3所示，具体实现步骤如下：
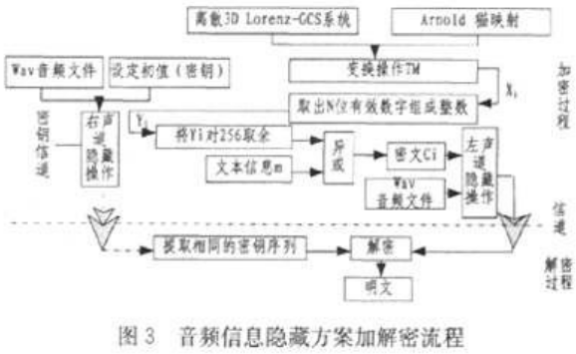
(1)加密过程：发送方A随机选取初始条件cx（o），y（0）∈BxXBy，用其驱动混沌系统(1)产生3D-Lorenz混沌序列码Chaosl，而后随机选取初始条件X'(O)∈B'x驱动混沌系统(2)产生Arnold混沌序列码Chaosz。用变换规则TM从Chaos1和Chaos2中提取出一组复合混沌源码M=TM(ChaOSl，ChaoS2)得到Xi。取出N位有效数字组成整数并对其进行256取余，把文本信息优变换成Te（m）。用公式C=E(M，Te(m)）加密明文P产生密文C，用Z=f((X(o)，y(O))，X1(0)）加密初始条件(X(0)，y(0))和X’(0)，其中E为加密函数。发送方A把密文C、初始条件Z分别隐藏到双声道语音信号的左声道和右声道的第7，8位上。最后A把隐藏密文和初始条件后的语音信号传给接收方B。
(2)解密过程：接收方B把密文C、初始条件Z分别隐藏到双声道语音信号的两个声道的第7，8位上分离出来。用初始条件(X(0)，y(O))、X7(0)分别驱动混沌系统(9)，(12)得到Chaos1，Chaos2，并利用(1)中通信双方在通信前约定的混沌序列的复合变换规则TM得到M。最终B用P=D(M，C)解出明文P和密文C，其中D为解密函数。
三、仿真实验
本方案采用matlab7.5仿真实现，伪装的语音信号为某流行歌曲的片段，分别对左声道进行密文信息隐藏，对右声道进行密钥隐藏。载体信号为双声道高保真音乐，采样频率为44.1okHz，量化精度16比特，位速1411kbps。需要加密传递的文本文件为txt文件，如图4(a)所示。
密钥集keys中取值分别为：
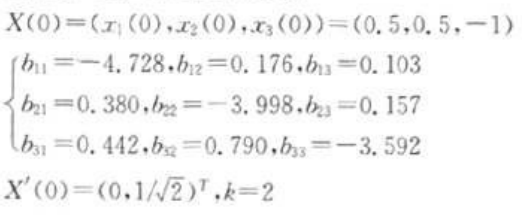
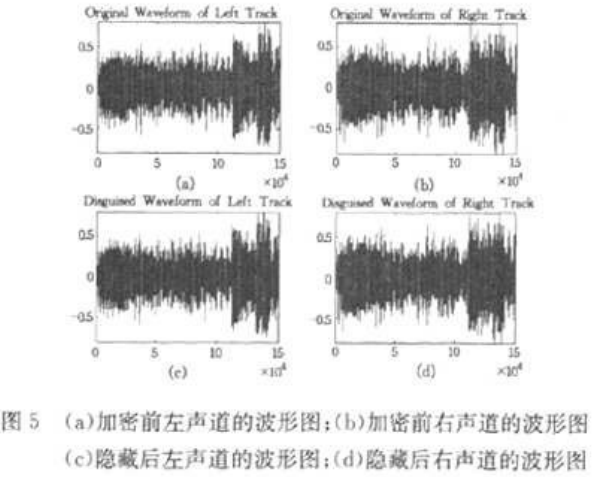
隐藏前后的语音信号波形如图5所示，由图可以看出，左右信号的相关性标准偏差没有任何变化，平均值仅有微小变化。待隐藏的被正确解密的文本为图4(b)。被隐藏的文本信息通过密钥组无损精确地恢复。若初值有微小扰动，混沌码就会有明显变化，对方将无法正确提取明文。如对密钥进行b11=b11+10-1-5扰动，则得到的解密结果如图4(c)所示，此时所解密的文本信息呈现乱码状态。
四、安全性分析
1、密文熵分析
香农提出了信息熵的概念，用以表征信源的不定度。对概率分布为(P1，P2，…．，Pn)的离散集，其信息熵定义为：
当信源概率分布为等概率分布时，信息熵能取到最大值log2（n）bit这就是最大熵原理。我们将利用变换将混沌流变为[o，255]之间的整数值，形成密钥流。我们可以用密钥流的信息熵来度量密钥流的不确定性的程度。当密钥流的概率分布为等概率分布时，即取[o，255]之间每一个值的概率均为l/256时，具有最大熵为1092256=8bit，也就是说信息熵越接近8，说明混沌码的随机性越好。
3D-Lorenz系统的混沌码的熵H1=7.9516
Arnold猫映射的熵H2=7.9561
同步系统的混沌码的熵H3 =7.9550
两个系统复合变换后混沌码的熵H=7.9571
从测试数据可以看到，GcS与Arnold猫映射两个系统经过变换后的复合系统，其混沌码的信息熵比任何单个系统的信息熵都更接近于8，说明复合系统所设计的混沌序列在随机性上比单个系统更有优越性。
2、相关性分析
本文实验测试中，对某一流行歌曲的片段进行实验，此处只对左声道进行信息隐藏，右声道无变化。载体信号为双声道高保真音乐，采样频率为44.1okHz，量化精度16比特，位速141Ikbps。图5(a)和(b)分别为原信号左右声道波形，(c)和(d)分别为隐藏信息的信号波形刚由于本实验只对左声道进行信息隐藏，因此右声道波形无变化。下面分别对隐藏前后左声道、隐藏前左右声道和隐藏后左右声道的相关性进行计算。
隐藏前后左声道的相关性为：
C1=9.999999999998264e-001
隐藏前左右声道的相关性为：
C2=4.106738302228002e-001
隐藏后左右声道的相关性为：
C3=4.=106738300576803e-001
从C1可以看出隐藏前后左声道的相关性接近1，说明隐藏信号前后左声道信息几乎无变化。从C2和C3可以看出，隐藏前后左右声道的相关性大小关系几乎维持不变。
3、密钥敏感性测试
本方案对密钥进行了敏感性测试。按以下步骤对3D-Lorenz系统初值x(o)及可逆矩阵B所构成的密钥组中的密钥进行微扰测试。
令舍弃初始迭代次数N-5000。将初始条件x(o)及参数B进行微扰，产生一维密钥流云，与未扰动时产生的一维密钥流c进行比较。取密钥流的长度为1250010（ASCII码）。密钥流云与e对应位的变化个数的百分比如表1所列。由表1得到三与c位变化个数的平均值为99.600%，非常接近于理想值的99.609%(255/256）。由此得出本文的密钥流生成器具有优质的伪随机性功能。
4、密钥空间分析
通过对密钥密感性测试的数值模拟表明，本算法对密钥集keys来讲，任何试图用微小偏差10-15来解密原始文本均是不可能的，因此本方案的密钥空间至少可达到10195，远大于提到的1045个密钥个数。此外，由于设计的同胚函数可以是不计其数的，使得密钥空间足以满足安全通讯的各种要求，对入侵者的强力攻击手段有很强的抵抗能力。
小知识之WAV
WAV为微软公司（Microsoft)开发的一种声音文件格式，它符合RIFF(Resource Interchange File Format)文件规范，用于保存Windows平台的音频信息资源，被Windows平台及其应用程序所广泛支持，该格式也支持MSADPCM，CCITT A LAW等多种压缩运算法，支持多种音频数字，取样频率和声道，标准格式化的WAV文件和CD格式一样，也是44.1K的取样频率，16位量化数字，因此在声音文件质量和CD相差无几！ WAV打开工具是WINDOWS的媒体播放器。
