全息图像文件加密之双随机编码正交映射

针对全息图像文件加密的要求，提出了一种双随机正交映射的全息图像加密算法。这种图像文件加密首先引入两个独立白噪声随机图像，通过双随机相位的加密，得到图像信号整个矩阵；接着引入哈德码矩阵把双随机相位的加密图像和正交矩阵的相位根据哈密尔顿算法束构造映射关系；最后经过扩束镜的物光波和密匙光波相互干涉，把频域的密钥和空域的密钥插入图像的灰度分量中。

一、双随机正交相位映射的加密方法

1、双随机过程

设原始实值图像为f(x，y)，图像大小为MxN，其中(x，y)为空域坐标，（ξ，η）为频域坐标，tp(x，y)为双随机相位的加密图像，p(x，y)和b(x，y)为均匀分布在[0.1]
之间的两个独立白噪声随机图像，其卷积以及均值都为0。则双随机相位的加密图像为：

式中：h(x，y)为脉冲响应；exp[jπp(x，y)]是能够产生相位在[0，2π]之间的相位掩模板；*为卷积运算符号；φ(x，y)是一个白噪声图像，其均值为o、方差为：

φ(x，y)包含了振幅和相位信息，是—个复数图像。

2、相位编码

假设复数图像集S包含l个像素信号，码长N，编码相位个数M，则第Z个信号可以表示为：

式中：n =1，2，…，N；l=1，2，…，L。

编码相位为：

于是图像信号矩阵为：

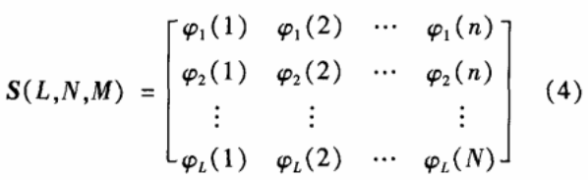
3、矩阵映射策略

随机生成N=2n维哈德码矩阵，与顺序排列(1，2，3．…，N)组成随机映射:

再生成—个N×N维哈德码矩阵，与顺序排列(1，2，3，…，NxN)组成随机映射：

矩阵的映射策略把双随机相位的加密图像和正交矩阵的相位根据哈密尔顿算法来构造映射关系。哈密尔顿算法是若矩阵A的特征多项式为：

则矩阵A满足自己的特征多项式：

通过预先得到的正交矩阵，然后将像素大集合X的一个元素分成埘块，每个块通过一个无冲突的散列函数映射成正交矩阵中的一个元素，再将ω个随机数进行异或：

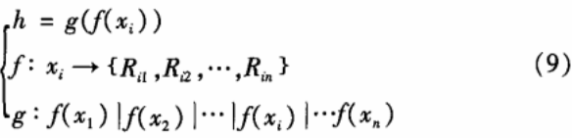
正交矩阵列A的元素(i，j)映射到加密图像中的元素点(i'，j’)中：

4、全息图像文件加密

设经过扩束镜后的第一路物光波复振幅为：

式中：t(x1，X2)为加密图像信息；φ为相位。

若激光的波长为λ，扩束镜距传感器距离为L1，物光波到图像传感器光面上复振幅变为：

菲涅尔衍射积分核为：

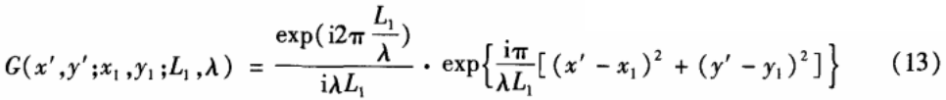
第二路密匙光波为R(x1，x2)=exp(φ(x1，x2)），扩束镜距传感器距离为L2，物光波到图像传感器光面上复振幅变为：

式中：FrT(．)为菲涅尔变换。

物光波和参考光波以菲涅尔衍射传播同时到图像传感器光面上，发生相互干涉，记录的干涉光场的强度为：

式中：*代表复共轭。

将宿主图像分解成exp[jφo（u，v）- jφrC(U，v)]3个灰度分量，将exp[jφo（u，v）- jφr(U，v)]插入其中的—个灰度分量中口设C0（u，v）是彩色图像一个归一化灰度分量，C(u，v)是加密图像，则：

式中：α∈[0，0.3]表示水印含量。

再将上述分量与其余量各分量合成为彩色图像。

5、加密算法流程

1)读入像素图像；

2)将该图像生成哈德码矩阵，用FFT生成傅里叶数字全息图；

3)读人另一幅大小相同的数字全息图，作加密矩阵；

4)全息图与加密矩阵点乘，得到加密数字全息图；

5)输出加密数字全息图。

二、仿真分析

实验以MATLAB为平台，以随机矩阵函数为加密函数，模拟光学过程生成非解密的图像。

将256×256像素大小的Lena图像（如图1）经过双随机相位编码隐藏到256 x256像素大小的图2中。

图3是空域的密钥，图4是频域的密钥，无论空域的密钥还是频域的密钥都是通过随机产生的，其密匙为32位，每一位均有随机正态分佰矩阵32 x32构成。

图5是空域与频域分别加密后的图像。在加密过程中运行，如果加密顺序不同，即先空域后频域或者后空域先频域，那么解密也需要按照此顺序才能正确解密，加密过程中空域和空域分别进行菲涅尔变换、相位哈密尔顿映射、双随机卷积。水印含最在空域和空域的含最均等，本文取0. 15。

图6是进行完全解密得到的解密图像。

图7是得到错误密匙解密后的结果，由于无法得到正确的密匙原函数，最终解密图像白噪声含量最多，与原图像相差较大。

图8是采用正确的频域的密钥而没有正确的空域的密钥情况下得到的图像，缺少最后一步解空域加密操作所得的解密网像，图像含有大最的局部噪声，图像与噪声混合后几乎淹没在噪声中，频域解密得到的图像在无法获得正确的空域密匙情况下空域解密，具有一定的盲目性。

图9是仅空域解密后的冈像，白噪声较多口用频域的密钥解密的结果与原图像之间的峰值信噪比相对较大，失真比较小些；而用频域的密钥解密的结果与原图像的峰值信噪比较小。通过比较可以看出，对待解密图像没有进行频域和空域解密将无法恢复原图像。

admin普通用户

海报分享