近十几年来,光学图像加密技术吸引了很多中外研究者的兴趣。其中很多算法中用到了随机位相作为密码,如比较经典的双随机位相编码。而多数图像加密是近三年来才出 现的一种图像加密方式,因为它能同时加密多幅图像而得到人们的关注。同时这种图像加密方式在信息的安全快速传输方面具有潜在的应用。
为此,我们提出了一种双图像加密算法,其原理是把两幅原始图像作为加密系统输入复函数的振幅和相位分布函数进行图像编码,然后对输入复函数进行随机分数傅里叶变换,得到一个频域的幅函数分布,分离出振幅作为加密图像而相应的位相部分则作为加密算法的密码,同时对这个加密算法的安全性进行了数值仿真分析。
一、图像加密算法
一般的图像加密算法是使用随机位相作加密系统的密码,本文尝试不使用额外的随机位相,用光学随机分数傅里叶变换来实现双图像加密。
1、图像加密算法
一个双图像加密算法如图1。
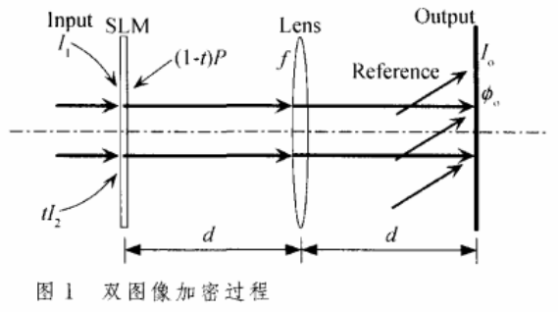
两个原始图像I1(x,y)和I2(x,y)分别被编码到表示输入平面光场的复振幅函数C(x,y)上,即:
![]()
这个编码过程的光学实现可以使用空间光调制器来完成振幅和相位的调制,而图像加密过程使用一次随机分数傅里叶变换来完成。
![]()
其中I0作为加密图像,符号§α表示随机分数傅里叶变换,(1-t)P是随机分数傅里叶变换的随机相位,作为算法的密码,0<t<1,0<P<2π,式中φ0的记录需要使用参考光束来完成,而随机分数傅里叶变换的输出相位φr0应是:
![]()
式中φ0是加密过程的中间量,而φ0r是加密过程最终的输出相位。
在随机分数傅里叶变换的光学实现中,在输出平面也需要一个随机位相调制,这部分操作在实际中可以对使用在线全息记录的位相调用计算机进行数据处理来获得加密的输出位相,而不必再使用空间光调制器来完成这个操作。
2、图像解密过程
图像解密过程就是图像加密的逆过程,联合I0,φ0r和密码(1-t)P执行一次逆随机分数傅里叶变换就可以解密出两幅原始图像I1和I2了。
二、加密算法的数值模拟
强度为0的像素点对于相位编码图像的相应像素位置的数值具有“湮没”作用:
![]()
这样,在解密时无法得到正确的位相信息,即图像在0像素位置增加一个较小的正数,即:
![]()
用两种类型(即简单文本图像和灰度级肖像)图像作为输入罔像用数值模拟方法验证这个双图像加密算法。在模拟中用到的四幅256×256像素的原始图像如图2。

其被分为四组进行测试,即g1={(a),(d)},g2={(b),(d)},g3={(c),(a)},g4={(c),(b)},对第一幅图像进行振幅编码,而对第二幅图像进行相位编码,四组测试中分数阶次选取的数值为a1=0.4,a2=0.5,a3=0.6,a4=0.7。而参量ε=1×104,t=0.1,所得的加密图像如图3。从图3可以看出来,在不同情况下所得的加密图像都有类似于白噪音图像。

图4给出了使用正确密码得到的恢复图像,其中各列图像对应着不同的分组,所有原始图像都被完好地恢复出来。

为了衡量解密图像和原始图像之间的相似程度,定义均方误差(MSE)函数:
![]()
式中I0和Ir分别表示原始图像和恢复图像的像素数值矩阵。而参量(M,N)是图像矩阵的行数和列数.图4中各图像相应的MSE值如表1。从表中可见,所有的MSE取值都很小,可以认为原始图像可以完好地被解密出来。

三、加密算法安全性讨论
近两年来,图像加密算法的安全性问题得到了很多研究者的关注,人们考虑了光学图像加密中的经典方案,即双随机相位编码技术的安全性问题。本文考虑密码在不同破解程度下加密图像的安全性问题。
首先考虑随机位相P在一定范围内的扰动(其它参量α,t选择正确的数值),即:
![]()
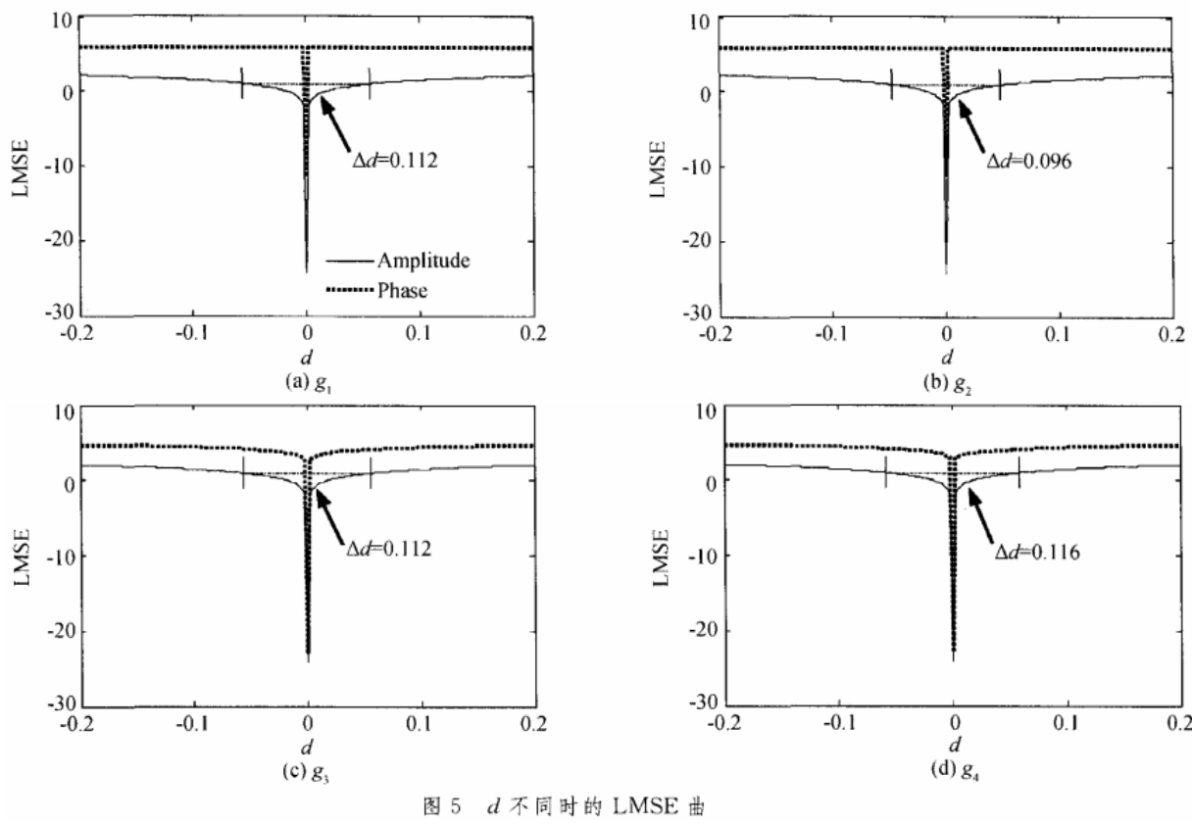
式中P和P'分别表示正确的相位值和扰动后的数值。d是扰动的振幅,而△P表示扰动的随机权重值,其值均匀地分布于区间(-1,1)。这样测试安全性的方式可以估计算法抵抗暴力破解的能力。四个分组在这样的模拟攻击下的MSE曲线如图5,其中y轴数值选取MSE的常用对数(即LMSE),本文认为MSE的阈值为10,在阈值以下意味着原始图像可以被解密。图5给出四组测试在这样的攻击下的LMSE曲线,其中实线标示的曲线对应振幅编码的图像,虚线对应相位编码的图像。实曲线在阈值以下部分d的变化范围△d显示于四个子图中,所有的△d都小于0.12。如果用随机相位变化区间[O,2π]估算,则算法的安全级近似为(2π/0. 12)256X256=52256X256,这是一个非常大的数字.而虚线标示的权限对应d的变化范围更小,四个分组d的变化范围要小于0.004,这说明编码于位相部分的图像具有更高的安全性,算法的安全级是较为理想的。
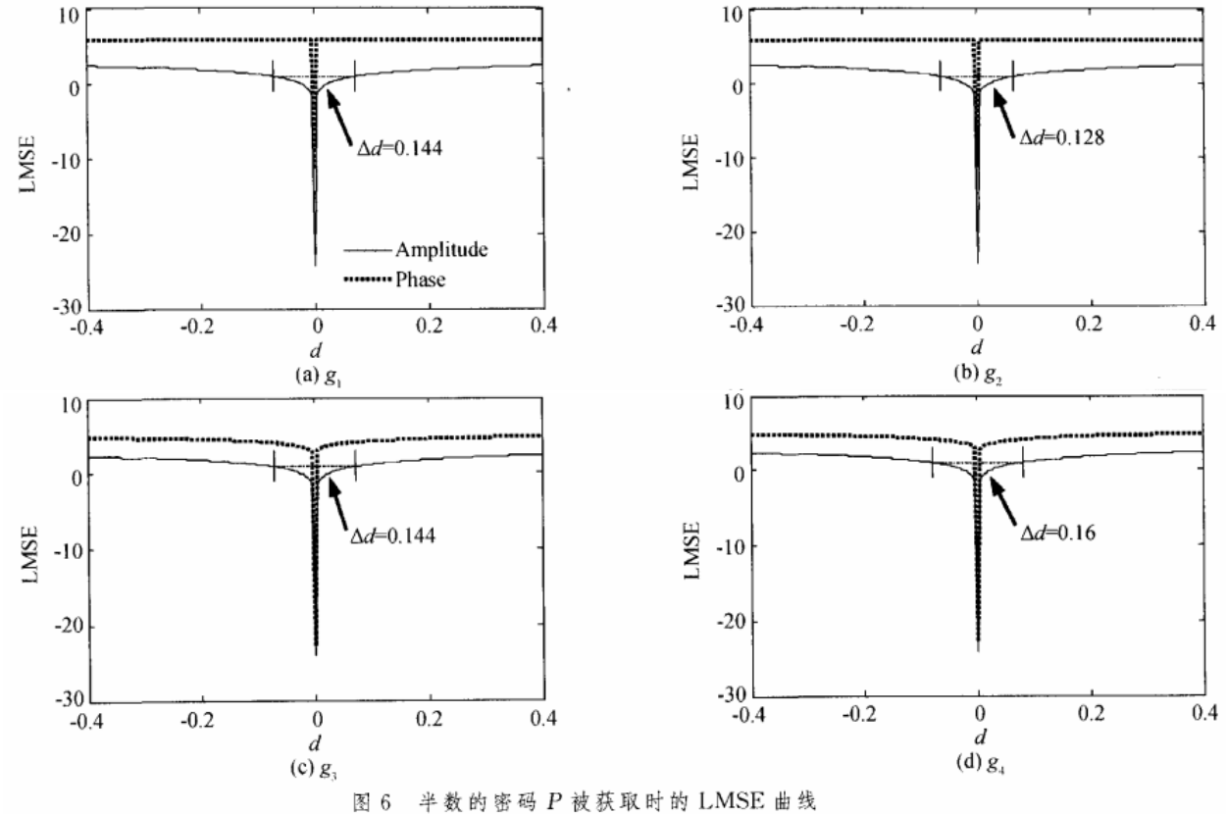
若随机矩阵△P的一半元素的值等于O,即半数的密码被攻击者获取(在模拟中选择矩阵△P下半部分的元素等于0),d在一定范围变化的结果。对应的LMSE曲线湿示于图6。从图6中可以发现△d的数值比图5中有所提高,但是编码到振幅的图像还是有一定的安全级。而编码到相位上的图像则具有较为理想的安全性。
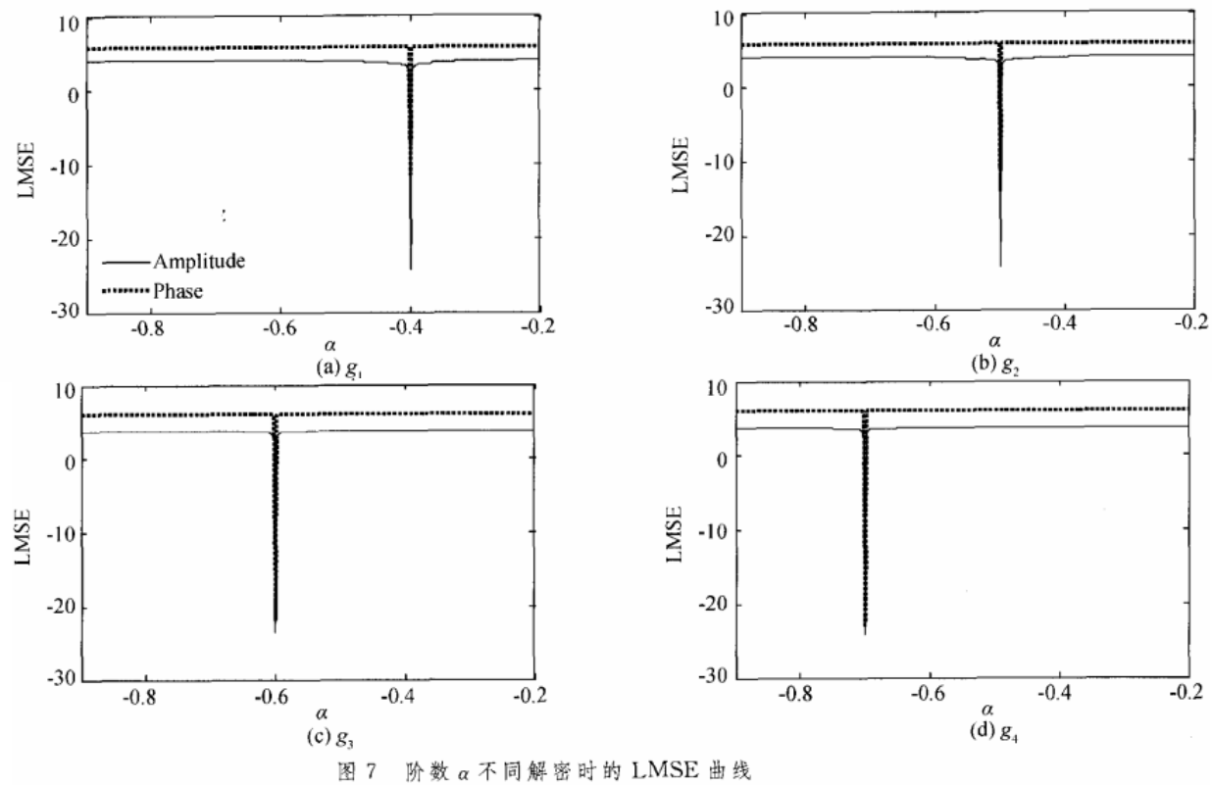
和分数傅里叶变换一样,随机分数傅里叶变换也具有分数阶这个参量。考虑随机相位被完全获知以及参量f的取值也是正确的情况时,变换的分数阶所能提供安全性的能力,所得的LMSE曲线如图7,其中计算时分数阶的步长选择0.002。可见编码到相位和振幅的图像所对应的曲线都是具有一个很窄的范围内,其宽度要小于0.004。而且在正确的分数阶次附近两幅原始图像被完好地恢复回来的,四个子图中的解密分数阶的位置与预先使用的分数阶是一致的,因为分数阶次仅仅是一个数值,更主要的密码还是要依靠随机相位。
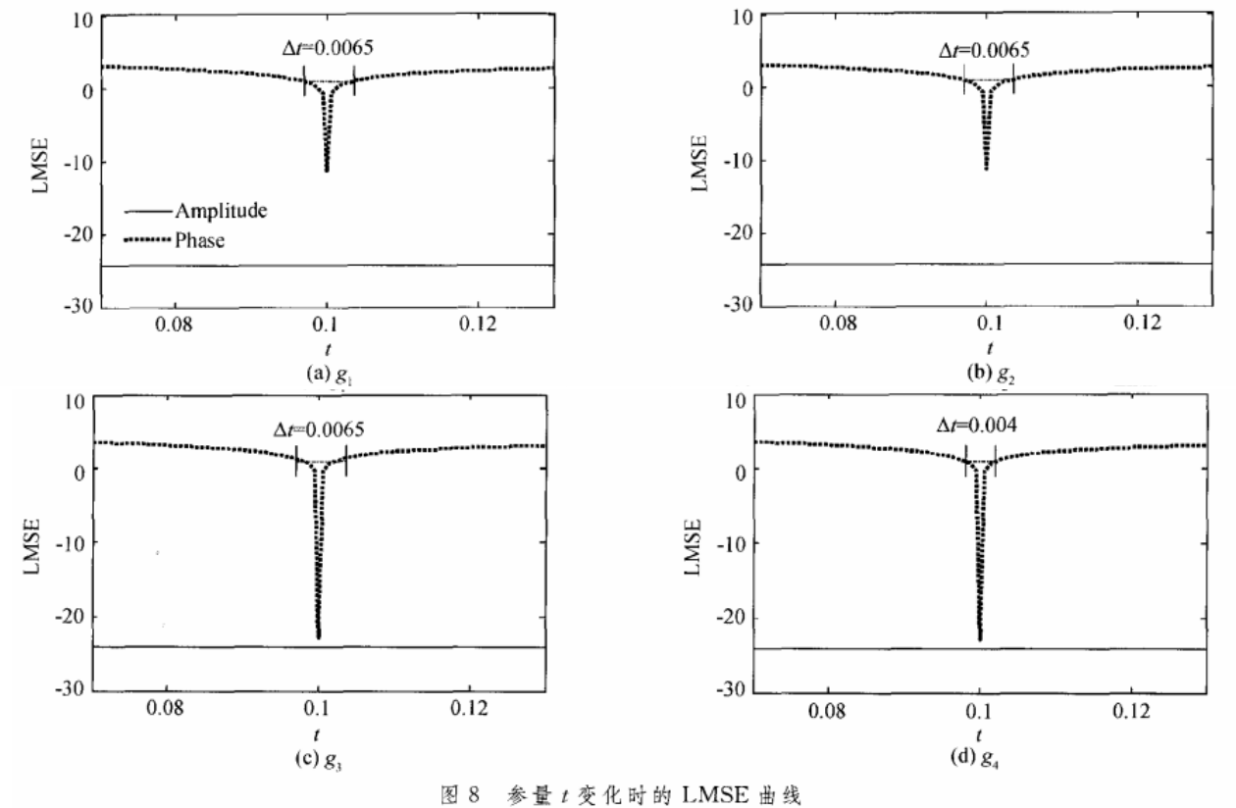
此外参量t对于编码到相位部分的图像也具有一定的密码作用。针对这种情况,假设t未知,而其它的参量已知(这时编码到振幅部分的图像可以完全被解密)。四个分组相应的LMSE曲线如图8。其中在阈值以下的范围△t是小于0.0065的,所以攻击者需要一定的努力才能解密编码于相位部分的图像,如果减小t的取值,△t还要相应地减小。
实际应用中,较为重要的图像应该首选编码到相位部分,因为这部分的安全级要高一些。而输入平面相位部分的编码特点类似于水印的思想(即原始图像与随机相位的权重叠加),这在一定程度上增加了对应原始图像的安全性。
小知识之相位编码
磁共振成像术语。磁共振成像中,为确定所选层面内自旋的位置,90°射频脉冲后间隔一段时间,在与层面选择梯度垂直的方向再施加一个梯度磁场(相位编码梯度),使沿该梯度方向自旋的相对相位发生变化。磁场越强,自旋进动频率越快,因此较强磁场中自旋偏转的角度比较弱磁场中自旋偏转的角度要大。经层面选择后,相位编码和梯度编码可共同确定层面中自旋的位置。








