随着网络技术的飞速发展,数字图像网络传输的安全问题日益突出,必须对图像进行加密保护。混沌系统具有良好的伪随机特性、轨道的不可预测性、对参数及初始状态的极端敏感性等特性,符合密码学的基本要求,因此基于混沌加密的系统成为人们研究的热点,目前基于混沌序列的图像加密,广泛使用的是logistic映射,而低维混沌系统的安全性不够高,因此高维混沌系统逐渐成为研究重点。
一些人构建了切延迟椭圆反射腔映射系统(TD-ERCS),一些人使用TD-ERCS混沌系统生成两个独立的伪随机序列赋给OCML系统的初值和耦合系数,取得了良好的加密效果,但计算量较大,方法不够简单快捷。为此我们尝试将TD-ERCS混沌系统作为像素灰度值改变操作的控制器,产生[o,1]的两列随机数.将这两列随机数作为混沌扩频序列转换到Z256空间中,利用扩展后的希尔密码,对图像像素值进行替代,本加密方案简单快捷,灰度直方图分析和像素相关性分析表明此方案加密性能较好。
一、TD-ERCS混沌系统
TD-ERCS系统映射关系为:
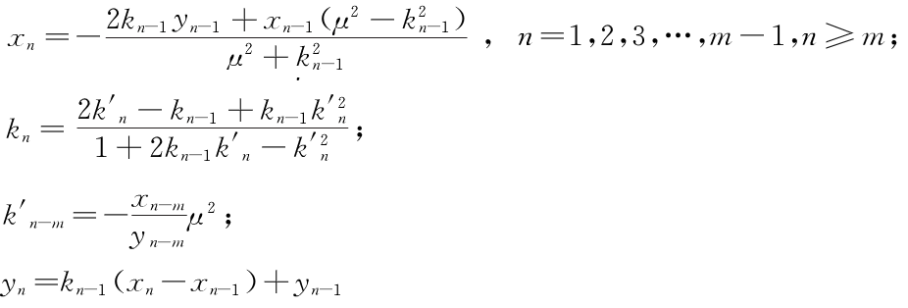
给定系统的种子参数(μ,xo,α,m),迭代后得到两个独立的数组序列xn和kn,当m>1时,只要迭代次数大于m+1,截取的序列具有高度随机性,m是对该系统混沌有重要影响的参数,本加密方案中将该系统的种子参数作为密钥控制参数。
二、加密算法
步骤1:输入TD-RECS的种子参数(μ,xo,α,m),迭代并舍去前200次过渡态后得到两组随机数列xn和kn,分别截取和图像素相同个数的随机数组成两个N×N的矩阵,将随机数列的第1-N的元素作为矩阵的第一行,将第(N×(i-l)+1)-(N×i)的元素作为矩阵的第i行,然后将矩阵乘以256后取整数,并对256求余,得到两个N×N的矩阵L1和L2,将这两个矩阵作为加密矩阵。
步骤2:选定待加密图像,读取其像素信息,设该图像大小为N×N的矩阵M。
步骤3:根据希尔密码算法,首先由Li矩阵对加密图像M进行第一次线形变换(即Y1=L1M),然后将所得结果对256求余得Y1;再由L2对Y1进行相同的操作(即y2=L2y1),从而得到加密结果。
三、实验结果与分析
本文对分辨率为256×256像素的Lena灰度图像和256×256的girl彩色图像进行算法仿真实验,仿真环境为Matlab7.0,实验中选取TD-ERCS系统的种子参数分别为μ=0.8,x0=0.9,α=0.75,m=6,采用第一类过渡态。
1、灰度直方图分析
一幅数字图像的灰度直方图可用于衡量加密算法的扰乱性,图1为灰度图Lena在加密前后的直观图和灰度直方图,从图1可看出,Lena原图像不同像素值的数目分布是不均等的;而加密后密文像素值在整个取值空间出现的几率趋于均等。
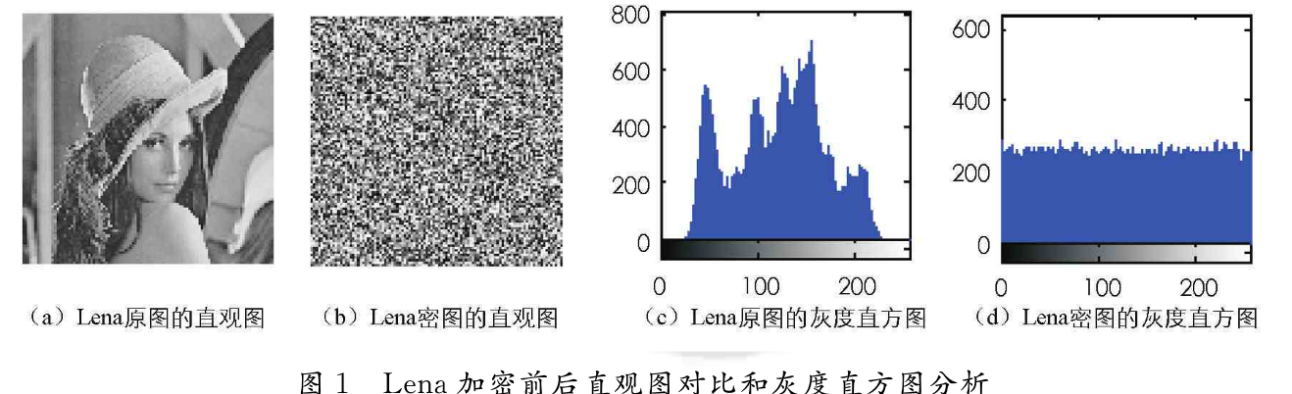
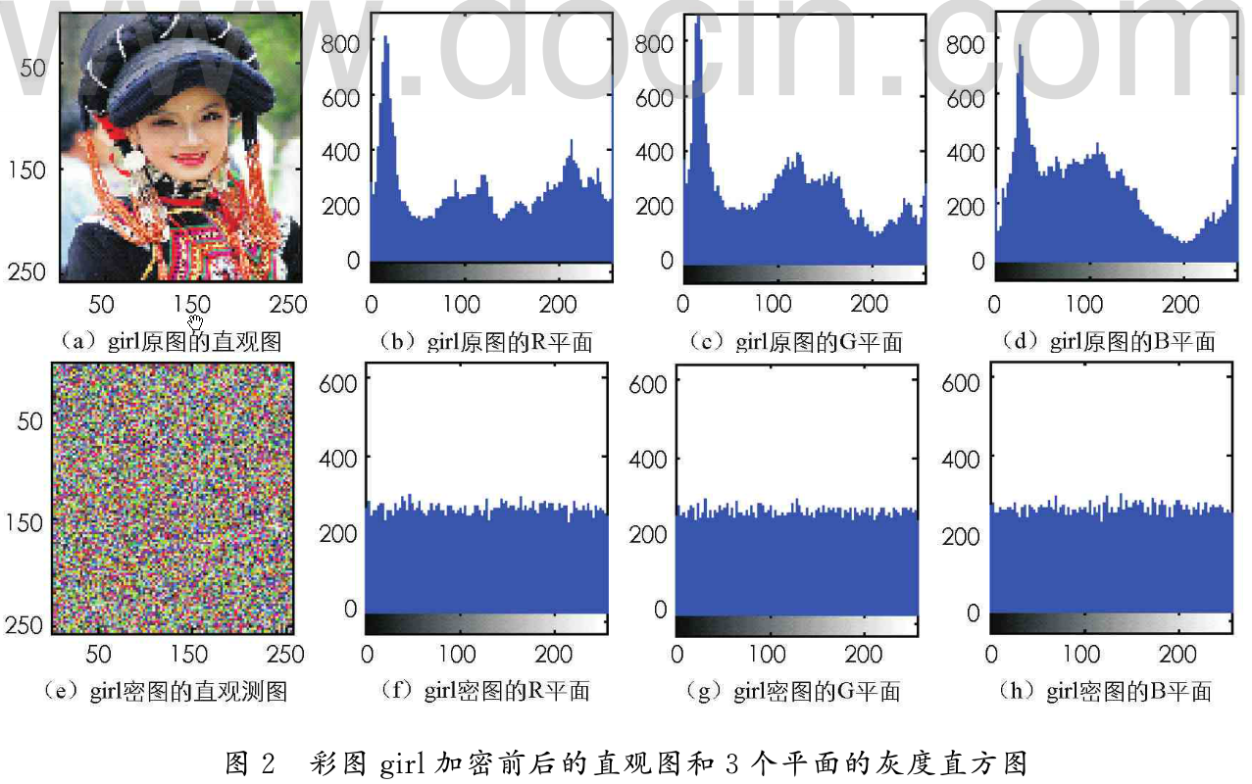
图2为彩图girl在加密前后的直观图和3个平面上的灰度直方图,图3为灰度图Lena加密前后的相关性,图2表明彩图girl加密后三基色平面的灰度直方图也均呈均匀分布,由此可知,不管是灰度图像还是彩色图像加密后都未保留任何明文信息,与采用空域与频域相结合的图像置乱方案相比,本方案对彩色图像加密有更好的扰乱性。
2、像素相关性分析
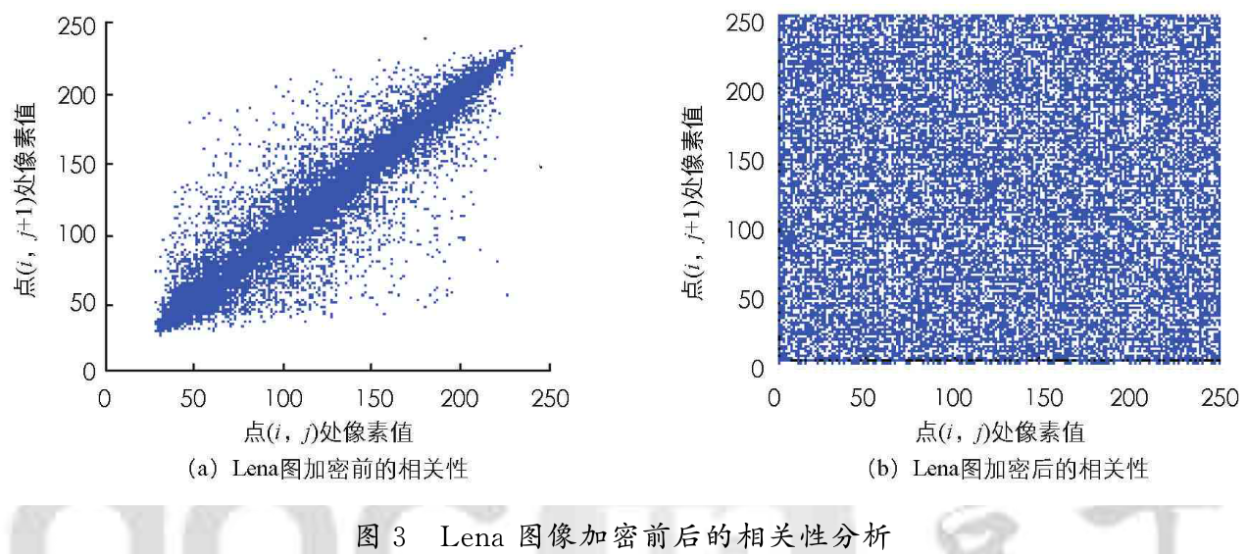
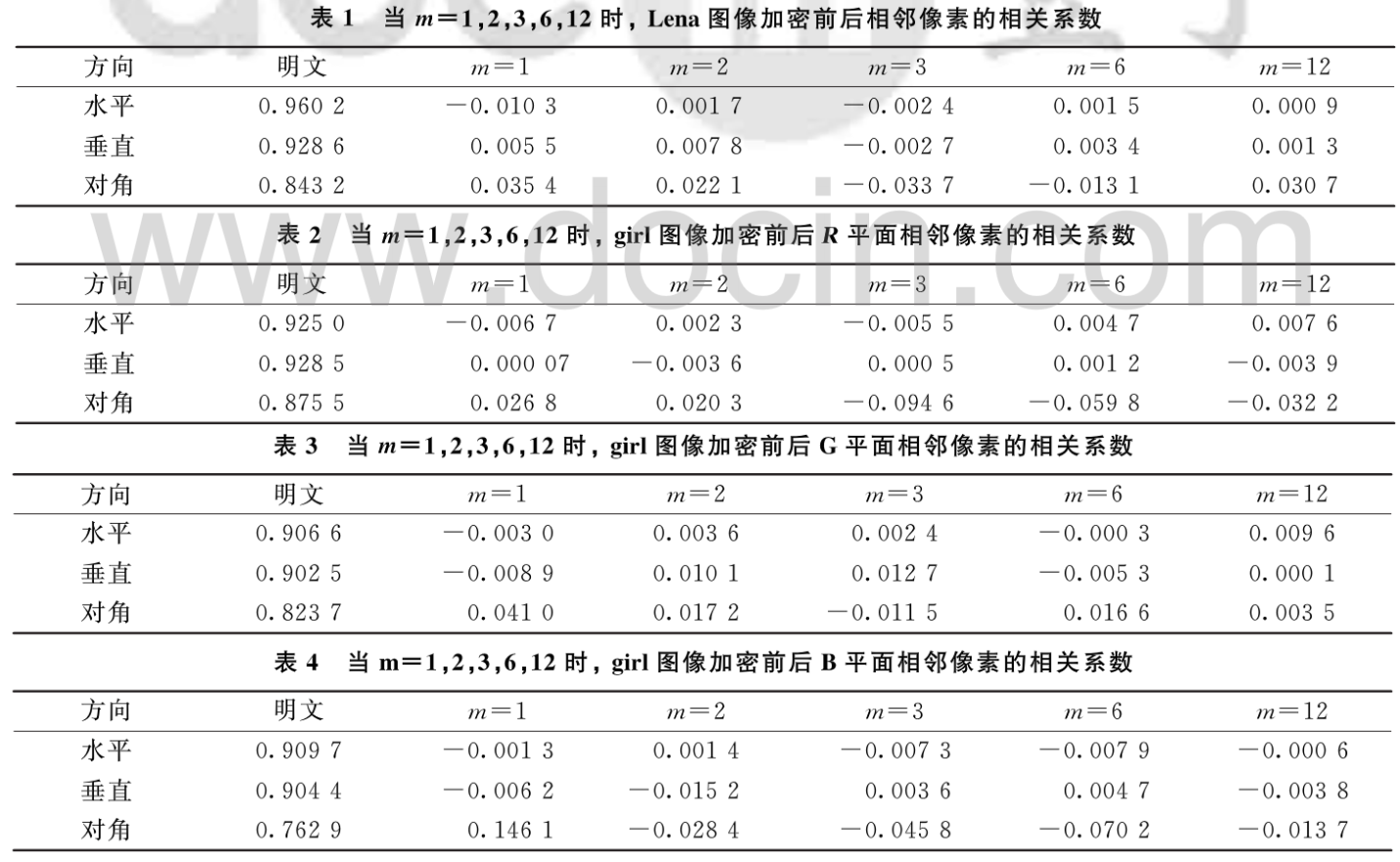
像素相关性分析是对加密算法的扩散性进行分析,图3给出了Lena图像加密前后水平方向相邻像素的相关性,由图3(a)知加密前像素点集中在对角线上,相关性很高,加密后像素点均匀扩散到整个像素空间(图3(b)),说明加密算法具有良好的扩展性,对girl彩色图像也可以得出与图3类似的相关性对照图,从Lena和girl图像中随机地选取水平、垂直、对角3个方向的相邻像素对,计算相邻像素在不同种子参数m下的相关系数,结果见表1-4。表1为灰度图Lena在不同种子参数m下加密的相关性对比;表2-4为彩图girl在不同种子参数m下加密前的相关性对比,从表1-4可以看出,3种方向计算所得的明文图像相邻像素的相关系数接近1,具有高度相关性;而加密后像素相关系数接近0,明文图像的统计特征已被扩散到随机的密文中;对比表中的统计结果可知,当m =12时密文各个方向上相关系数都较小,所以选取m=12,扩散性比较好,安全性较高。
小知识之过渡态
过渡态(英文:Transition state)是基元反应反应坐标中能量最高的一点所对应的分子构型。处于过渡态的分子也称为活化络合物。理论上,活化络合物是极不稳定的,它向反应物和产物转化的概率相等;[1]绝对的不可逆反应中,在过渡态这一时刻,所有的碰撞分子都会转化为产物。[2]根据量子力学理论,活化络合物布居为零,过渡态是能量最高的一点,任何扰动都会导致它的改变,故无法分离出来,也是无法观测到的。











