针对单一混沌加密系统对灰度图像进行加密存在加密强度不够,留有轮廓这一问题。我们给出了一种应用二维Arnold矩阵变换和混沌理论混合加密灰度图像的全新算法,它巧妙的利用Amold扰乱图像位置的特点,结合混沌加密理论,有效地解决了单一混沌加密灰度图像加密强度不够的弱点。
一、单一混沌理论的加密技术
1、混沌映射
一类简单又被广泛研究的动力系统是Logistic映射一其定义如下:
![]()
混沌动力系统的研究工作指出,当e=(3.469...,4]时,Logistic映射工作于混沌状态。这可由计算机描绘的Feigenbaum分叉图看出图1(a)。
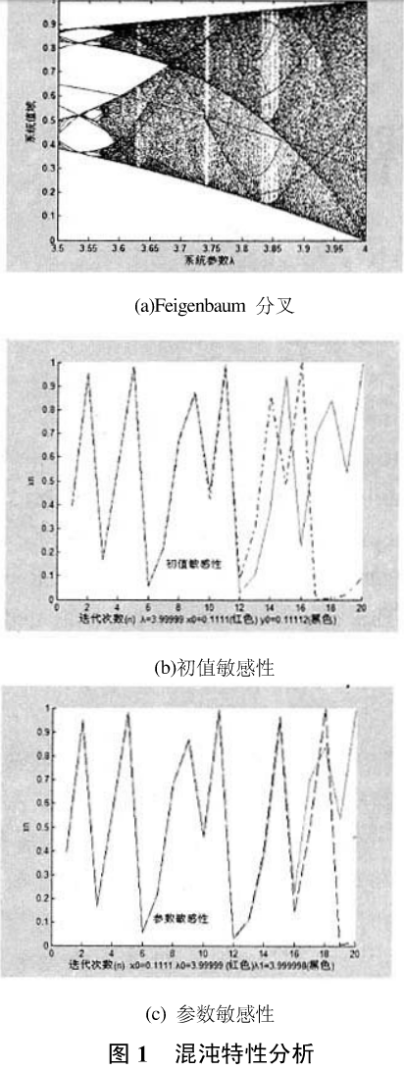
Logistic映射在混沌状态下具有很好的初值敏感性和参数敏感性,图1(b)给出初始值分别为X0=0.111(红线),Yo==0.11112(黑线)情况下,对应的Logistic映射输出值图1(c)给出参数初始值分别为eo=3.99999(红线),e1=3.999998黑线)情况下Logistic映射输出值一由于混沌具有这些良好的性质,因而被广泛的应用于各个安全领域。
2、基于Logistic映射序列的图像加密解密算法
(1)打开一个文件并过滤头信息;
(2)从文件中以bit为单位读图片数据g;
(3)根据迭代方程Xn+1=eXn(1-Xn)生成混沌序列{xi},并获得一个比特c,e为控制参数,Ifxi>=0.5then Sii else Si=e(i=1,2,...,8);c=xi;
(4)通过异或计算:e=g Xor c,获得密文比特e;
(5)把e写到一个新文件中;
(6)重复(1)到(5)直到文件结束。
3、混沌加密效果图
实验参数e=3.988888,x0为方程Xo=3.988888*XO*(1-Xo)迭代10 000次后的结果,从加密图像图2(b)效果来看,对灰度图像加密很不理想。

为改善混沌流加密对灰度图像的加密效果,需要结合其它加密理论,文中采用结合二维Arnold矩阵变换方法。
二、Arnold变换思想
设像素的坐标xY=S{0,1,2...N-1}
1、加密步骤
二维Arnold变换为:
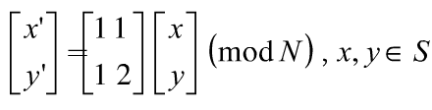
记变换矩阵为A,反复进行这一变换,测有迭代公式:
![]()
式中:
![]()
为迭代第终步时点的位置。
2、解密步骤
由于Arnold变换具有周期性一只要对密文图像继续迭代T(T=Mn(n))次可恢复原图像。n为加密时相应的密钥一周期表如表1所示。
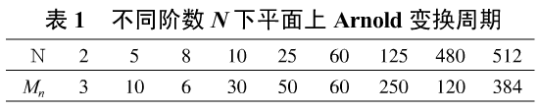
分析:Arnold变换可以看作是裁减和拼接的过程,通过这一变换将离散化的数字图像矩阵s中的点重新排列一进而实现图像位置扰乱。
若单一采用Arnold变换矩阵加密图像,由于动力系统固有的特性。在迭代进行到一定步数时会恢复到原来的位置,即变换具有庞加莱回复性。这样,只要知道加密算法,按照密文空间的任意一个状态来进行迭代,都会在有限步内恢复明文。这种攻击对于现代计算机来说计算时间是很短的,因而,躲密性不高,不能完全依赖其加密图像。因此,本文用其作为混合加密的第一步。
3、改进的Arnold变换
为增强Arnold变换加密效果,密钥n采用动态管理机制,即采用单向哈希函数动态生成函数为:
![]()
式中,ai是参数k是素数一且后取值接近于N阶图像变换周期的一半,f(.)是单向哈希函数,用变换矩阵进行一定数量的[x,y]T作用后更新密钥n,使得同一明文不同阶段作用得到的密文不同。
三、混合加密系统的设计
设计的加密方案基于两个步骤,首先利用改进二维Arnold变换打乱图像像素的位置,再利用混沌理论对置乱的图像进行混沌流加密。
1、加密步骤
(1)初始准备 Arnold变换初始密钥no,单向哈希函数参数ai,i=0,...m和k以及每一密钥船能够作用的像素个数t混沌参数e和x0。
(2)图像数据利用改进的Amold变换进行扰乱。
(3)对扰乱的图像进行混沌流式加密。
2、解密步骤
(1)对混合加密的图像进行混沌解密。
(2)对第一步得到的数据实施改进的Arnold逆变换即继续迭代num=(周期T-加密密钥n次),加密结果如图3所示。

四、混合加密的安全性分析
(1)线性攻击和差分攻击属于对分组加密的攻击法一对混沌流加密攻击是无效的。
(2)统计分析攻击法的防范:因为混沌密文0,1的分布概率是完全不确定的,明文的统计性完全扩散了。
(3)对选择明文雇文攻击法的防范:由于异或运算的特殊性,混沌自身的单向,密钥处理迭代的多重构造一所以密钥流的推断是不可能的。
(4)对图像的分层攻击法的防范:对原始图像首先采用二维Arnold变换,打乱原始图像轮廓使分层攻击毫无效果。
小知识之矩阵变换
在线性代数中,矩阵的初等变换是指以下三种变换类型:
(1) 交换矩阵的两行(列);
(2) 以一个非零数k乘矩阵的某一行(列);
(3) 把矩阵的某一行(列)的z倍加于另一行(列)上。
容易看出,这三种初等变换都不会改变一个方阵A的行列式的非零性,所以如果一个矩阵是方阵,我们可以通过看出等变换后的矩阵是否可逆,来判断原矩阵是否可逆。当然,这只是矩阵初等变换的一个小小的应用,它在线性代数中的更重要的应用主要体现在以下几点:求矩阵的秩,求向量组的极大无关组、秩,求解线性方程组,求多项式的最大公因式等。







