gyrator变换全息图是利用gyrator变换快速算法模拟实现了gyrator变换全息图的产生和再现,并研究了基于相移数字全息的gyrator变换全息图,在此基础上提出了采用正弦相位光栅实现光学图像加密的新方法,该方法利用gyrator变换在相空间的旋转特性,将gyrator变换的角度、光栅的频率及光栅的旋转角度作为加密密钥,并利用两个或两个以上的gyrator变换系统的级联实现图像加密,增加了系统的安全性。
一、gyrator变换及其光学实现
函数f(x,y)的GT的数学形式定义如下:

式(1)中Gα(*)表示旋转角度为α的GT,Kα(u,v;x,y)为变换核,(u,v)为空间频率坐标,(x,y)为空间位置坐标,当α=O时,Gα(*)为恒等变换;当α=π/2时,Gα(*)为坐标交换的傅里叶变换,GT的旋转角度α具有可加性和周期性。
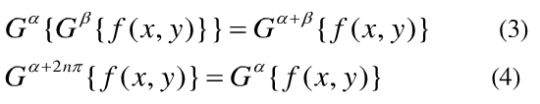
而Gα{*}的逆变换为G-α{*},根据式(4),有:
![]()
可以将式(5)作为旋转角度为α的GT逆变换形式。
GT的光学实现形式是由三个广义柱透镜级联形成的光学系统,如图1,图1(a)为三个广义柱透镜级联形成的透镜组光学系统,透镜组中广义透镜之间的距离相同,都为z。广义透镜l1和广义透镜l3的焦距同为z。广义透镜l2的焦距为z/2。P1和P2分别为输入平面和输出平面。
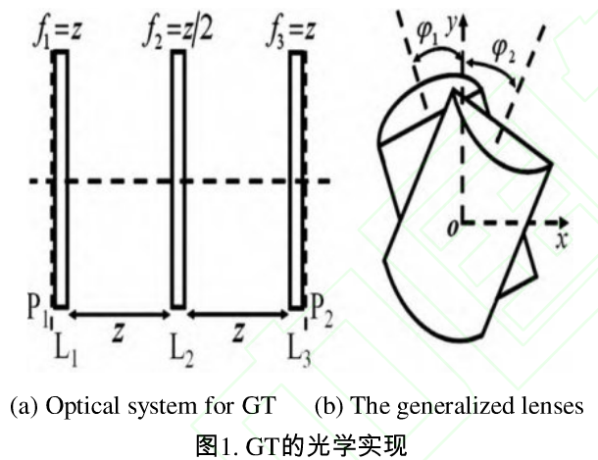
图l(b)为广义透镜的结构,这里的广义透镜是由两个相同的会聚柱面透镜旋转一定的角度紧贴在一起构成的,其中φ1和φ2分别为两柱面透镜对称轴相对于oy轴所旋转的角度,且满足:
![]()
输入平面上的光波复振幅f(x,y)通过这个光学系统的变换作用,在输出平面得到复振幅分布为:
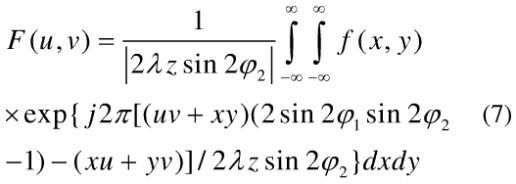
式(7)中λ为光波波长,如果令:
![]()
则在引入坐标量纲归一化因子√λz的条件下,式(7)与式(1)是完全一样的。
二、GT全息图
根据光学全息的原理,GTH是物体在单色平面波的照明下,利用GT的光学实现系统,通过一定角度的GT后生成的物光波的GT波面与平面参考光波在GT域平面进行干涉,用全息的方法记录下的物光波的GT波面的复振幅分布I再现时,用参考光波照明全息图,再经过相应角度的逆GT,在系统的输出平面得到物体的再现像。
1、GT全息图的记录和再现

GTH记录光路如图2(a)。图中Iai,i(i=1,2,3)表示构成变换角度为α的广义透镜,用单色平面光波照明物平面O上的输入图像f(x,y),在变换角度为α的GT域平面H上,引入参考光R(u,v)和图像的GT光场F(u,V)=Gα(*){f(r,y)}进行干涉,得到输入图像的GTH的光强分布为:
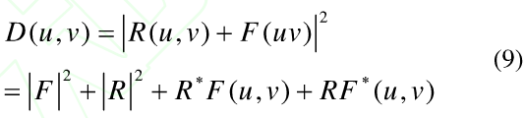
经线性处理后的全息图的振幅透过率H(u,v)和D(u,v)成正比
![]()
k为比例常量,再现时的光路如图2(b)。图中L-α,i(i=1,2,3)表示构成变换角度为-α的广义透镜,用参考光波作为入射光波照明物平面上的全息图H(u,v),透射光场为:
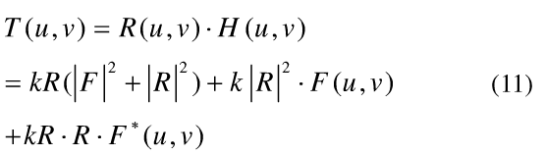
透射光场经过变换角度为-α的GT光学系统后,在成像平面上的光场分布为:
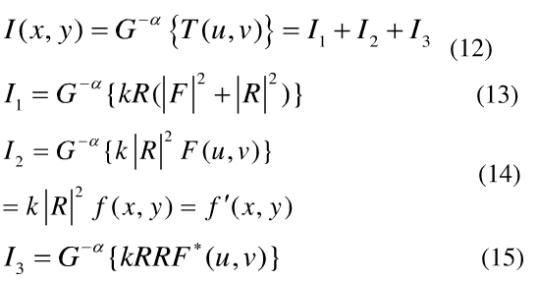
式中I1为衍射零级;I2为衍射正一级,是原图像的再现像;I3为衍射负一级,在变换角度不等于π/2时,通常为一个模糊的像,模糊的程度与变换角度偏离π/2的程度有关。
如果对透射光场施行角度为α’=α-π的GT,则成像平向上的光强分布为:
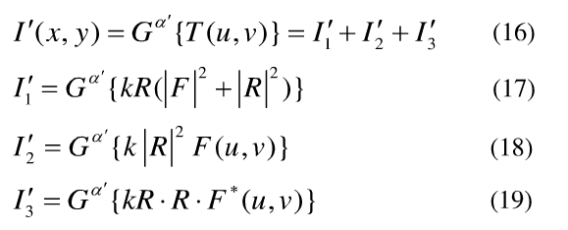
对于输入图像而言,f(x,y)是一个实数函数,则f*(u,v)可以表达为:
![]()
则:
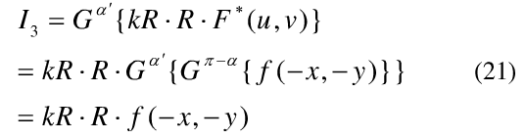
可见,对透射光施行与记录时的变换角度耐目匹配的另一变换角度d'=α-π,将得到与原图像相反的像f(-x,-y),类似菲涅尔全息的共轭像再现,这是GTH的一个显著特点。
2、数值模拟实验
为了验证提出的GTH的可行性,在GT快速算法的基础上模拟了GTH。模拟实验中,所用光波波长为λ=632.8nm,输人物体为512x512像素的二值图像(图3(a)),GT的角度分别为α=25°、45°、75°、85°、88°和90°,参考光与光轴夹角为θ=1.6°,物光与参考光的强度比为1:3,数值模拟结果如图3所示。为简便仅给出变换角度为75°的全息图(图3(b)),各个变换角度相应的再现结果依次由图3(c)至图3(h)给出:而图3(i)则是图3(b)在变换角为105 0的GT下再现共轭像的结果。

从GTH的记录过程可见,GTH与傅里叶变换全息图和菲涅耳全息图既不同而又有相似之处。傅里叶变换全息图记录的是物的频谱,菲涅耳全息图记录的是物光波前,GTH记录的则是物光波经GT的波前o GT域上的场分布既与物函数有关,又与变换角度有关,而后者由式(8)决定于广义透镜的结构参数。从GTH再现物体的像的方式上看,它用原参考光照明全息图,使全息图再现的波前再经过一逆变换系统成像,再现方式与一般的傅里叶变换全息图相同。从GTH再现像的分布上看,小角度的GTH再现的衍射O级分布的面积较大,对衍射正一级形成了较大的噪声干扰:随着变换角度的增大,衍射0级分布的面积逐渐减小,当变换角度接近90°时,衍射0级就收缩到观察平面中央很小的一个矩形区域,而变换角为90°时,GTH就退化为傅里叶变换全息图,其再现结果和傅里叶变换全息图的再现结果是完全一样的;在变换角度不等于90°,再现的衍射O级的形状为一个“#”形的分布,这是GT所特有的一种分布。因此,GTH图既区别于一般的菲涅耳全息图,又有别于一般的傅里叶变换全息图。
3、消除衍射零级及共轭像的gyrator变换全息图
同其他全息图一样,要应用GTH必须消除再现时衍射0级和共轭像对于再现的原像的干扰。目前能较好地消除衍射0级和共轭像的技术是相移数字全息术,将其应用于GTH中,相应的光路如图4所示。
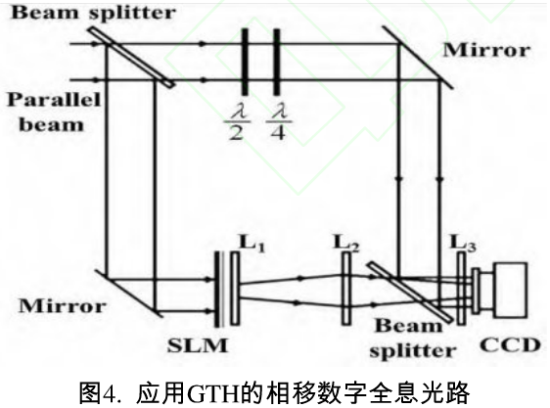
通过调整平行参考光路中凇波片和M波片快慢轴的相对位置关系可以获得相移值分别为0、π/2、π和3π/2的四幅全息图H1(x,y)、H2(X,y)、H3(X,y)和H4(X,y),设参考光波共轭光波在干涉平面的复振幅分布为R‘(x,y),利用四步相移算法可得干涉平面处物光波复振幅分布为:
![]()
按照图4的光路,以512x512像素的图像作为输入图像(图5(a)),假设CCD幅面大小为512x512个像素,像元尺寸为6.45Umx6.45μm,物光与参考光的夹角为3.6°,物光与参考光的强度比为1:3,入射单色平面光波波长为632.8μm,利用GT数值算法,模拟在变换角度为45°时所进行的四步相移数字全息,得到的全息图像为图5(c)(为简便只给出一幅数字全息图),由数字全息图计算得到的复值图像的振幅和相位分别为图5(d)和图5(e),而由复值图像进行再现的结果如图5(f)所示。从再现结果可以看到,再现的图像有轻微的模糊,但图像的细节还是能清楚的分辨(如帽子的褶皱和帽檐线等),再现图像还带有轻微的双曲线型条纹噪声(图像下部),对图像信息的整体影响不大,双曲线型噪声可通过GT域滤波得以消除。从再现像的结果可以看到,衍射0级和共轭像的干扰已被消除。图5(b)是原图像的GT结果,对比图5(c),可以看到全息图明显出现了双曲线型的干涉条纹,而由全息图计算出的复值图像的振幅和相位都带有双曲线型条纹噪声,这就是再现像中带有双曲线型条纹噪声的原因,这是由GT产生的。进一步的实验表明,当逆GT角度和原变换角度一致时,双曲线型噪声将得到减弱或消除:而当逆GT的变换角度和原变换角度有差异时,双曲线型噪声将会增强,变换角度的差异过大时将使图像难以辨认。

三、gyrator变换全息图在光学图像加密中的应用
在GT提出之后,GT能够应用于图像加密中,多次迭代的GT操作能实现图像加密,并给出了应用两次迭代GT的图像加密算法和数值结果。将迭代GT的图像加密方法推广应用于光学图像加密系统中,尽管描述了采用干涉的方法来记录,但是他们都没有给出相应的GTH,所有的结果都是数学算法上的数值结果。
在本文提出的GTH的基础上,应用图4的四步相移干涉数字全息方案,提出了一种采用正弦相位光栅实现GT光学图像加密的新方法。
1、采用正弦相位光栅的数字全息加密系统
双随机相位编码的图像加密技术,其基本思想是:利用随机相位掩膜在变换域捋待加密图像的傅里叶域频率信息的分布扰乱而获得振幅和相位都接近于白噪声的加密图像,实现加密。因此,在进行图像加密时只要想办法在变换域扰乱图像的傅里叶域频率信息就能达到加密的目的,而为了解密,则要求变换域是可逆的。GT是可逆的变换,GT的一个重要特征是使二维信号在相空间中发生位置坐标一空间频率坐标的一种扭曲旋转(又称为cross-gyrator),即GT在相空间的旋转不是通常意义上的相平面(x,M)和相平面(y,v)的旋转(如傅里叶变换和分数傅里叶变换等),而是相平面(x,v)和相平面(y,v)的旋转,这种旋转改变了信号原有的位置坐标一空间频率坐标的对应关系,这就为扰乱信号的傅里叶频谱提供了一个天然的平台。但仅施行GT还不能完全扰乱信号的傅里叶频谱,若能先让信号的傅里叶频谱发生某一角度的旋转再施行GT,则信号的傅里叶频谱会很大程度上被扰乱,若多次重复这一过程,并且使每次傅里叶频谱的旋转角度和GT角度都不一样,则输入信号的傅里叶频谱就会被完全扰乱。光学中的e调制实验表明,用不同取向的光栅调制后的图像其傅里叶谱将按光栅调制方向旋转,因而可以采用正弦相位光栅实现对待加密图像的傅里叶频谱的旋转。
图6是本文提出的采用正弦相位光栅实现GT光学图像加密光路的示意图。这是两个子系统的级联形成的光路,每一单独的子系统由正弦相位光栅和GT系统组合后形成,光栅平面为GT系统的输入平面,而后一级的输入平面为前一级的输出平面,整个加密系统的输入图像由空间光调制器SLM1产生,光栅分别用两个空间光调制器SLM2和SLM3产生,而SLM1和SLM2紧密连接,系统的输出是由CCD来记录物光与参考光的干涉图像。用这部分光路取代图4中物光的GT部分即可采用相移数字全息的方法记录加密图像的数字全息图。
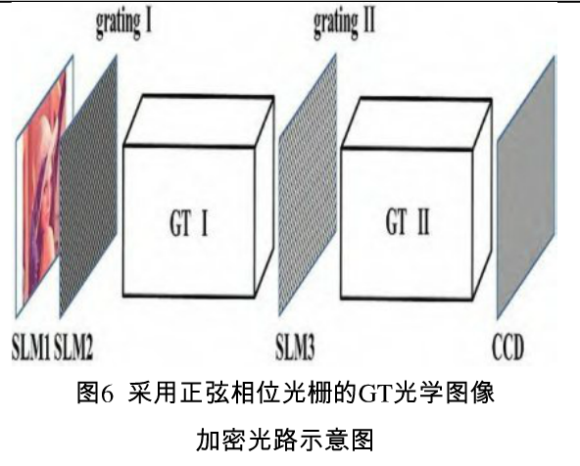
正弦相位光栅由空间光调制器(SLM)产生,如德国HoIoEye公司生产的Holoeye LC2002液晶SLM在一定条件的情况下,对于入射的光波,从检偏器出射的光与入射到液晶的光可以出现兀以上的相位变化,因而只需将送入到SLM的正弦光栅强度图像调制到相位输出的模式即可。而正弦光栅强度图像可用如下方法产生:
设SLM的像素尺寸是WxH(W>H),构造一个大小为nWxnW( n=2,3,4_)的图像平面,图像的水平坐标0和nW-1分别对应的角度为0和兀,这样将角度区间[0,兀]离散化为nW点,每个点的角度值为:
则构造光栅图像的每一列的数值为Zk=siri(f·Xk)(f为光栅频率),将构造的光栅图像逆时针旋转角度φ后截取图像中央区域大小为WxH的图像作为正弦光栅强度图像送人SLM。这样产生的光栅包含由如下参数:W、φ、n、f和H,只有所有参数相同时,按上述方法产生的正弦光栅才相同,为简便,我们可以默认加密和解密过程中所有的光栅的W、H、n参数都相同,而光栅函数可以表达为S(x,y;f,φ)。
按照图6的加密光路,利用正弦相位光栅进行GT光学加密的数学算法描述如下:
设GT系统I和GT系统II的变换角度分别为α1和α2,输入的图像函数为q(x,y),两个正弦相位光栅的相位分布函数分别为:
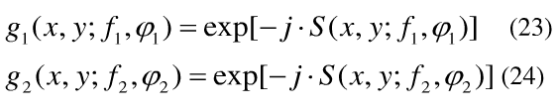
其相应的相位共轭函数为:
![]()
![]()
则加密过程:
![]()
解密过程为:
![]()
采用相移数字全息方案时,CCD记录的是加密图像Q(u,v)的数字全息图,而解密时的复函数Q(u,v)则由相移数字全息算法计算得到,解密过程完全在计算机中计算完成。
2、仿真实验及性能分析
依据式(27)和(28),综合图4和图6,对本文提出的在相移数字全息的基础上采用正弦相位光栅实现GT光学图像加密的方法进行数值模拟。仍以图5的模拟参数作为基本的光学参数,假定所用空间光调制器的分辨率都为512x512,像素尺寸为32μmx32μm,产生光栅时,参数n=3,两个正弦光栅grating I(图7(b))和grating II(图7(c))的参数分别为:
![]()
GTI的变换角度为α1=50°,GTII的变换角度为α2=167°,实验结果如图7所示。为了简便,图像被加密后的四幅相移数字全息图只给出其中一幅(图7(d)),从全息图上不能得到原图像的信息,而从数字全息图恹复的复值加密图像的振幅(图7(e))和相位(图7(f))也得不到原图像信息,并且相位图像接近白噪声。图7(g)是在各个加密参数(a1,a2,f1,f2,φ)都正确的解密结果,解密图像除了有轻微的模糊和舍有噪声外,与原图像是一致的。图7(h)-(k)分别是a2,ai,f2和仇错误的解密结果,可以看
到这四个参数任意一个错误都不能得到正确的解密结果。

可以用两幅图像的相关系数(CC)来评价本文所提出的加密方法的性能。如果以O(x,y)和D(x,y)分别代表原图和解密图像,那么两幅图像的CC应该为:
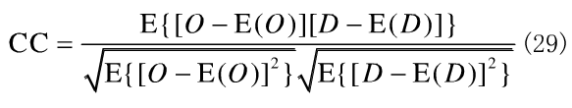
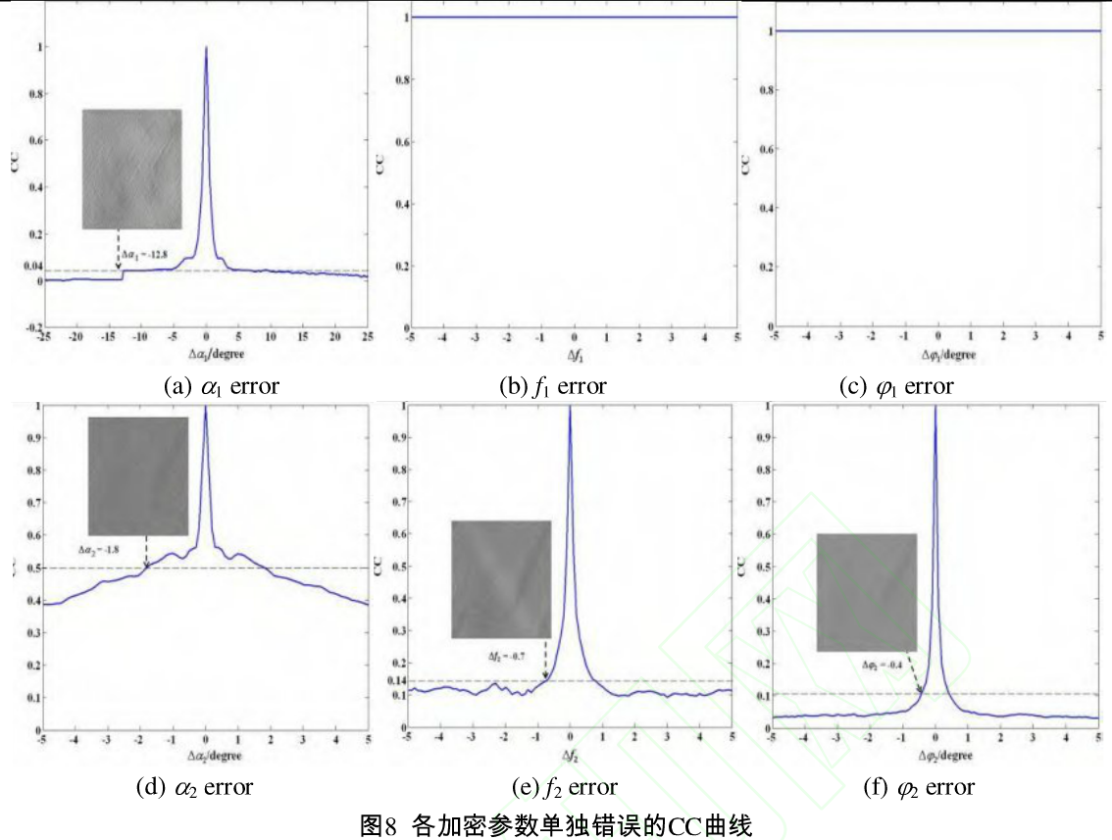
这里E{*}表示求期望值运算。据此考察了在解密时各个加密参数单独错误的CC,如图8所示。从图中可以看到,解密时第一级的GT系统中角度的错误对解密结果影响不大,只有在变换角度错误较大时(|△α1|>12.8°,图8(a))才产生无法辨认的解密结果:而第一级正弦相位光栅的错误则对于解密结果毫无影响(图8(b)、(c))。解密时第二级的Grr系统中角度的错误对解密结果影响较大,在|△α2|> 1.80时(图8(d)),解密的图像已经无法辨认:而第二级正弦相位光栅的错误对解密结果影响很大,光栅频率错误达到0.7或光栅的旋转角度错误达0.40时,解密图像和原图像的CC就降低到了0.1左右,解密图像不可辨认(图8(e)、(f))。由此可看到,第二级GT系统对整个加密系统的安全性起着决定作用,第二级GT系统的三个参数(α2,f2,φ)是具有良好安全性能的加密密钥,进一步的实验表明,当采用多级GT系统级联时,加密系统的密钥空间会增大,加密系统的安全性能会得到更大的提高。
小知识之全息图
全息图,是以激光为光源,用全景照相机将被摄体记录在高分辨率的全息胶片上构成的图。以干涉条纹形式存在。用同种激光照射,胶片前后方可出现原景物的虚实两个立体影像,视角不同,所见影像也不同。全息图是一种三维图像,它与传统的照片有很大的区别。传统的照片呈现的是真实的物理图像,而全息图则包含了被记录物体的尺寸、形状、亮度和对比度等信息。这些信息储存在一个很微小但却很复杂的干涉模式中。这个干涉模式是由激光产生的。











