利用Logistic映射、Henon映射与超混沌M-G系统构造了一类嵌套混沌变参映射,并通过Lyapunov指数证明所构造映射产生信号的混沌性,同时分析其相关性和功率谱特性,然后利用其输出的混沌信号构成图像加密所需要的符号矩阵和灰度矩阵,与经过小波压缩后的图像运算,从而完成图像文件加密。
一、嵌套变参映射构造及混沌性分析
Logistic映射是一种单峰的混沌映射,见式(1):
![]()
其中1 .401155<a2表示沿该方向扩展,反之,则是收缩。
因此Lyapunov指数给出混沌过程对初始条件的敏感依赖性的度量,同时正值的描述了混沌系统相空间混沌吸引子内部各个轨线之间的不稳定性,研究也证实了在判别一个系统是否存在混沌运动的时候,只要判别其最大Lyapunov指数是否为正的即可。
对于多维相空间情况下一般有多个正的i值,它的运动情况将会更复杂,因此就把那些Lyapunov指数正值比较大,包含正的Lyapunov指数有两个正的或者更多正的Lyapunov指数时的系统称为超混沌。M-G混沌系统就是一个超混沌系统,但它是一个时滞超混沌系统,而非时滞超混沌系统,它的正的Lyapunov指数不会超过系统的维数,如果要产生更复杂的混沌信号,那必然就要增加系统的结构从而增加维数来使系统具有更大的正的Lyapunov指数,但这种改造对于混沌系统应用于信息和保密通信系统往往是代价太大,不实用。
而本文利用的超混沌系统M-G十分简单,系统正的Lyapunov指数不受限与系统维数,它可以产生很多正的Lyapunov指数,从而产生超混沌信号。
对本文中的B系统分析当参数变化的时候其混沌性。由系统方程可初步分析此系统至少有两个正的Lyapunov指数,因为它是一个三维系统,且是两个混沌系统嵌套而成的。固定参数b=0.3,利用“伯内廷”方法分析当a参数变化时候系统各变量的Lyapunov指数,可以得到随参数变化的指数谱。
可以看出系统Z变量信号与X变量信号的Lyapunov指数变化趋势是大概一致的,这也可以从系统关于Z变量方程中得知,Z变量是X变量做了非线性运算得到的,故当X变量输出为混沌信号的时候,Z变量也输出混沌信号,同时从Lyapunov指数比较而得Z变量的混沌信号比X变量混沌信号的指数大,因此更加复杂,而且c参数的取值只要保证平衡性即可,无特殊要求范围,因此c的范围可以很大。另外当a取一定的参数时候,如1.35时候可以使Y变量也输出混沌信号,那么此时就是一个超混沌系统了,利用这时的系统进行通信系统信息传输,保密性将更强。
二、混沌时间序列分析
B系统映射参数的选取按照如下方式。所构造映射中的参数分别按照M-G系统的Fl00(对应系统参数p=0.2、m=10、n=0.1)和俨l0(对应系统参数p=10、m=10、τ=-2)时间延迟取相应M-G系统参数下其输出的混沌信号中的值来取,为了仿真方便,这里取相应时延内的输出某两个固定值,Fl00对应a-1.3,c-2,τ=10对应a-l.4,τ-2,然后由嵌套变参映射输出混沌时间序列。以下图像加密所用的符号矩阵与灰度矩阵所需要的混沌信号,就由此参数下的嵌套变参映射输出信号构成。
混沌序列信号不满足绝对可和与能量可积的条件,但功率谱有限可积,因此可以通过功率谱来研究其频域特性。周期变量的功率谱呈现分离尖峰结构,尖峰对应的频率之间存在公倍数;拟周期变量对应的各尖峰间无公倍数现象;混沌和噪声的功率谱在宽的频率范围内都呈现出连续性,因此,若系统的功率谱是连续的时候,说明系统具有混沌特征的可能性。因为混沌吸引子内部存在很多不稳定周期轨道,因此如果若连续谱中除了显现噪声特性外,还具有宽峰谱特性时,那么就是混沌信号的谱。
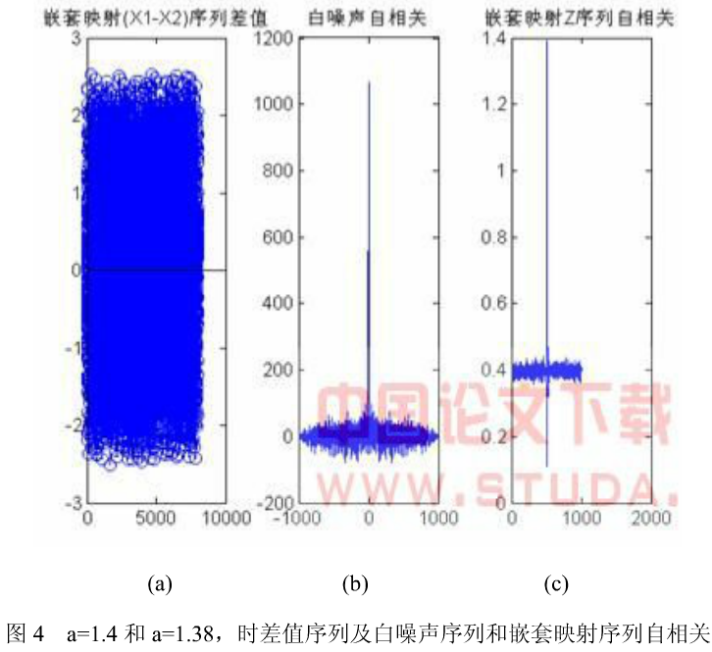
通过计算,可以发现映射所输出序列的自相关和白噪声类似,随机性和互相关性在取不同参数的时候,也非常弱。参数分别选a=1.4和a=1.38,b、c参数不变化的时候序列的差值信号见图1 (a),可见参数很小的变化输出序列差别极大,反映了参数敏感性,因此在图像与文件加密中有大量的加密数据和密钥可用,且无任何联系。图1 (b)、(c)分别是白噪声和输出Z序列的自相关,可见非常尖锐,证明其类噪声性质。
三、数字图像文件加密过程
(1)利用小波包变换的技术对原始图像进行压缩,去除图像中大量的空间冗余信息,降低图像数据之间的相关性,可提高信息传输的有效性和抗破译性。图像矩阵设为I。
(2)利用嵌套变参混沌映射输出的实值混沌序列Xn,yn,并利用Xn ,yn生成符号矩阵s和灰度矩阵w,如式(6)0 S(Xk),W(yk)分别代表符号矩阵和和灰度矩阵里面的元
素,把这些元素构造成和图像矩阵相同维数矩阵即可。
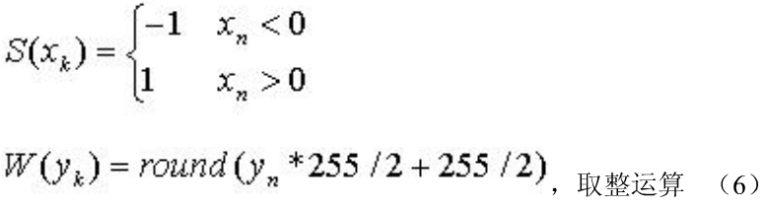
(3)灰度置乱矩阵B实现过程:设图像矩阵中的元素为I(i,j),灰度矩阵元素W(m,n),则灰度置乱矩阵B(p,q)生成如下,见式子(7):
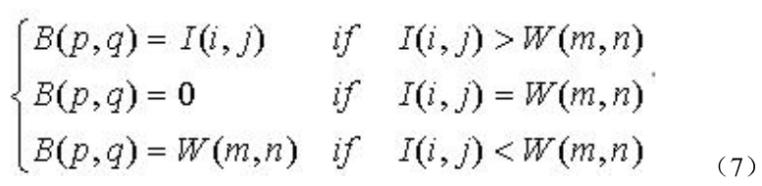
(4)加密过程:(B+w).S,既灰度置乱矩阵与由混沌信号构造而成的灰度矩阵再相加,然后与符号矩阵相乘即可。
以上加密过程如图2(a)(b)(c)分别是原图像、压缩图像和加密后图像,图2 (d)是当生成符号和灰度矩阵的嵌套映射的参数a相差10-3的时候恢复的图像,可见参数极微
小的变化就不能正确恢复图像,原因就是由于在加密的过程中,不但把原图像的灰度矩阵用混沌信号生成的新矩阵置换了,而且还又和其做了相加运算,可以证明这时候其灰度矩阵元素序列就是混沌信号。经过大量图像加密验证,证明本加密方法不但实现简单而且还有很好的抗破译性。另外本加密方法可用的密钥可以是系统的参数a、b、c和确定系统参数M-G系统的参数p、111、n与其系统时延共同确定,只要其参数在能保证输出混沌特性的参数变化范围内都是可以的。
解密过程为以上加密的逆向运算。

本文利用了三种混沌系统构造了一种嵌套映射,其中Logistic映射、Henon映射相互嵌套构造成新的离散系统,系统中参数变化由超混沌系统M-G系统确定,参数取某值时间的长短M-G系统的时间延迟来确定,不同的延迟时间内又对应不同的M-G系统输出来确定系统这段时间内的参数,所以系统的变化可以非常复杂。又经过Lyapunov指数方法证明系统在一定的参数变化范围内的混沌特性,因此当通过M-G系统来控制这些系统的参数变化的时候,系统输出就可以是变化多样的混沌信号,如果用其加密所要传输的信息,系统的抗破译性非常强。
小知识之嵌套
嵌套-在已有的表格、图像或图层中再加进去一个或多个表格、图像或图层,这种方法就叫做嵌套。











