离散的Logistic映射对初值和结构参数的改变具有极端的牧感性,在一定条件下能够产生混沌,并且产生的混沌序列具有类白噪声统计特性等特点。同时利用数字图像本身的特点和人类视觉系统酌特性,先对原始图像进行压缩,再用混沌序列进行加密和传榆图像,这样不仅可以减少存储空间,还可以提高加密和传输效率。本文基于以上特性提出了一个新的基于Logistic混沌序列的数字图像文件加密算法。
一、混沌系统
混沌现象是在非线性动力系统中出现的确定性的、类似随机的过程,这种过程既非周期又不收敛,并且对初始值有极其敏感的依赖性。从时域上看,混沌映射得到的序列类似于随机序列。相关性较弱,具有很好的类白噪声特性,因此可以用来产生伪随机信号或伪随机码。原理上只要增加迭代次数,伪随机码的周期可以很长,产生长码十分简单。通过混沌系统对初始值和结构参散的敏感依赖性,可以提供数量众多、非相关、类随机而又确定可再生的信号。基于上述特点,混沌已广泛应用于保密通讯中,同时也可以作为加密序列。混沌加密技术已成为一种新兴的加密技术。
1、混沌的定义
设(X,p)是一致的度量空间f:X→X是连续映射,称f在X上是混沌的,如果(D1):其有对初值敏感依赖性;(D2):f在X上拓扑传递;(D3):f的周期点在X中稠密。
其中,具有对初值敏感依赖性是指:∃δ>0。使∀x∈X,及x的领域N(X)。∃y∈N(x)及n≥0使P(fn(X),(fn(y)>δ;f在X上拓扑传递性是指:∀U,U开集,vcx,∃K>0。
通常情况下,可以采用Lyapunov指数、功率谱分析或Pioncare截面法来识别系统是否进入混沌状忐。
2、Logistic映射的混沌特性和统计特性
Logistic映射是一个源于人口统计的动力学系统,其系统方程可写为如下形式:
![]()
其中xn为映射变量,μ斗为系统参量,它们的取值范围分别为:-1<xn<1,0<μ<2。Logistic映射是一一个非常简单,却又具有重要意义的非线性迭代方程,它具有确定的形式,并且系统不包含仟何随机因素,但系统却能产生看似完全随机的,对参量μ的动态,变化和初值极为敏感的现象。
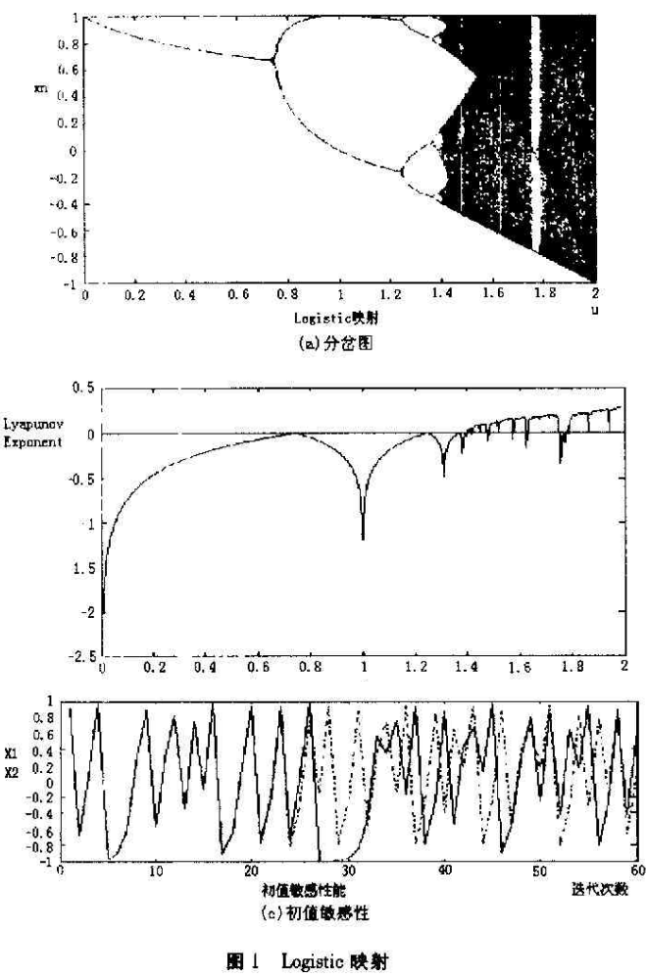
图1中(a)是Logistic映射的分岔图,可以看到随着参数p的变化,不断出现倍周期分岔,直至出现混沌状态;
(b)是Lyapunov指教曲线图,正的Lyapunmr指数表明运动的轨道在每个局部都不稳定,相邻轨道指数分离。因j此它可以作为系统混沌的判据。在Lyapunov指数为零时,出现分岔;
(c)表明了Logistic映射对初始条件有极端的敏感性,图中的实线是在xicr-0.202时的曲线,虚线是在X20;0.2020000J时的曲线,尽管两个初值相差甚微.但在迭代25次后。两个值就截然不同了。因此为了确保可靠性,人们在应用时应舍去前而一段过渡过程。
系统(1)产生的序列的概率分布函数为:
![]()
其中p(x)是不依赖于初始值的,他对混沌系统具有普遍适用性。
人们可以利用概率分布函数来计算混沌系统(1)的均值、自相关系效、互相关系数等统计特性。其中均值为:
![]()
自相关函数:
![]()
设取两个初始值x0和y0,那么序列的互相关函数为:
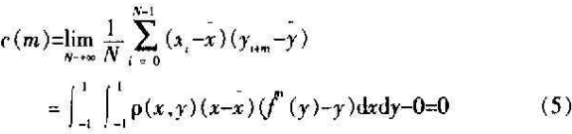
以上特性表明,尽管混沌动力学系统具有确定性,其遍历统计特性等同于白噪声,因而可以应用于包括数字通讯和多媒体数据安全等众多应用领域的噪声调制。
二、基于Logistic的数字图像文件加密方法
1、加密算法原理
加密算法往往可以写成以下的变换式:
![]()
其中明文x,密文Y和密钥Z分别是有限氏度的字符序列Lx、Ly和Lz,他们的长度可以不相等,方程(6)强调一个密文y通过加密系统Ez与一个明文X对应,函数由密钥的值来决定,Ez称为加密算法。
一般的数字图像包含大量的数据,但这些数据是高度相关的,对予静止图像往往含有大量的空间冗余信息。在该文提出的算法中,把Logistic映射的初始值xo、结构参数p和过渡过程参数作为密钥,根据密钥产生相应的混沌序列xk和yk,然后,由xk和yk生成相应符号矩阵S和灰度矩阵G,实现对数字图像文件的加密。
2、加密算法设计
加密算法的模型如图2所示。
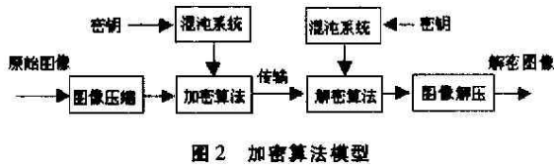
(1)符号矩阵S的生成
利用生成的实值混沌序列xk,通过定义阈值来产生符号序列sign(xk):
![]()
根据压缩后Sign(xk)的大小按行或按列生成符号矩阵S,即Smn=MxN。S由混沌序列生成,因此它也是混沌的。
(2)灰度矩阵G的生成
利用生成的实值混沌序列yk,通过如下的变换生成序列g,使得g[0,256],并根据压缩后图像的大小,生成相应的灰度矩阵G。同理Gmn-MxN也是混沌的。
![]()
3、加密算法实现
加密算法的基本步骤如下所示:
(1)对原始图像I进行压缩,可以采用基于DCT、FFT或小波变换的压缩技术;
(2)根据压缩后的图像,由密钥x0产生相应的实值混沌序列xk和yk;
(3)由xk和yk生成符号矩阵S和灰度矩阵G;
(4)将压缩后的图像W和G进行位异或,得到WG;
(5)将WG和符号矩阵S进行点乘,得到加密网像WGS,完成加密过程。
解密算法的实现:
根据密钥,把加密过程逆向运算即可获得解密图像。
三、仿真实例分析和结论
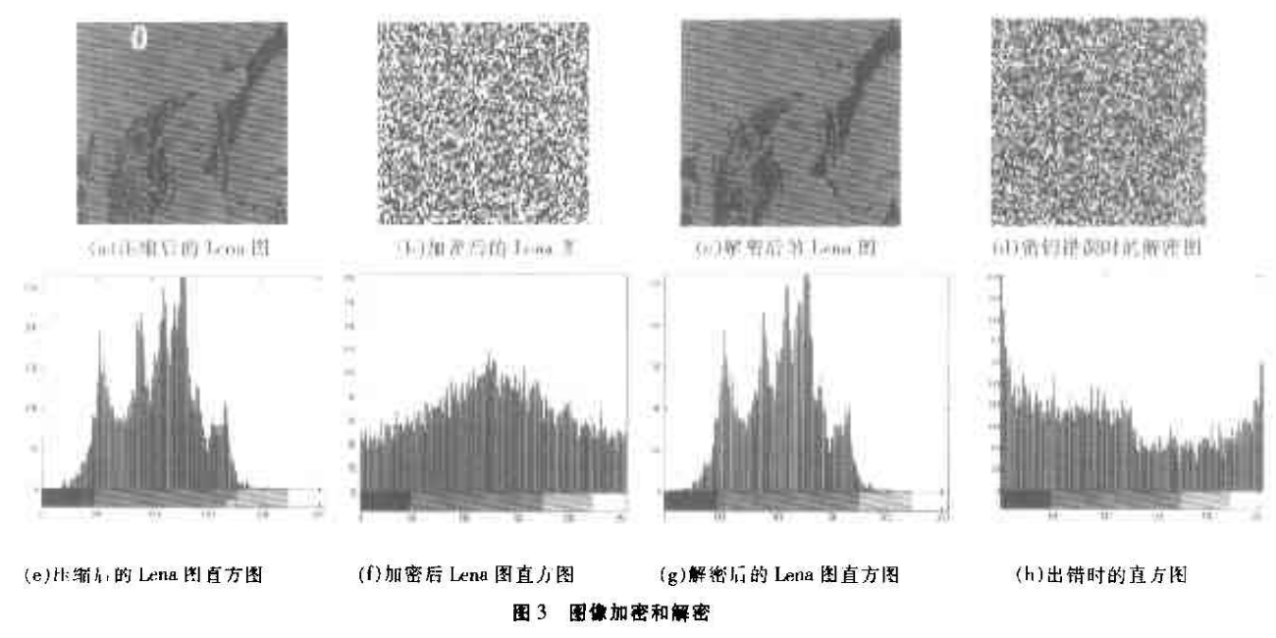
采用该文的算法对多幅图像进行试验,原始图像为256x256的Iena图,图3中(a)是对原始图像进行小波压缩后的图像,其大小为135x135。文中选取x0=0.422J2,μ=2.去掉过渡过程前60个点作为密钥对图像进行混沌加密,图3(b)是经过加密后的图像,可以看到图中已没有一点原始图像的信息了,图3(c)是输入正确的密钥进行解密后得到的图像,它与加密前的图像完全一致。图3(d)是在x0=0.42213,μ=2和去掉过渡过程前60个点作为密钥对图像进行解密腈得到的图像可以看到即使是很微小的误差,解密后的图像已完全不同了,同样当取不同的μ值或者不同的过渡过程,也不能对图像做正确解密。
小知识之DCT
是一种与傅立叶变换紧密相关的数学运算。在傅立叶级数展开式中,如果被展开的函数是实偶函数,那么其傅立叶级数中只包含余弦项,再将其离散化可导出余弦变换,因此称之为离散余弦变换。











