图像加密算法之三维猫映射

混沌序列具有易于生成、对初值敏感和类白噪声的性质，因而适合应用于密码系统设计。为此我们将二维猫映射推广到三维，并综合运用一堆无限折叠、Chebyshev、Lorenz等三种较复杂的混沌映射，共同产生密钥，对图像文件进行加密。

一、混沌系统

混沌是非线性学科的一个重要方面。它是一种貌似无规则的运动，是在确定性非线性系统中，不需要附加任何随机因素就可出现类似随机的行为（内在的随机性）。混沌系统最大的特点就在于系统的演化对初始条件十分敏感，因此从长期意义上讲，系统具有未来不可预测性。

1、Chebyshev映射

Chebyshev映射是一种以阶数k为参数的映射，其离散化形式定义如下：

其中xn ∈(-1，1)，其概率分布函数PDF为：

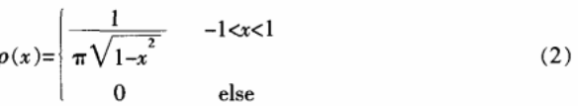
ρ(x)为偶函数，由混沌信号的各态历经性，可以用集平均代替时间平均，即：

定理1若独立选取两个初始值xoyo，则产生混沌序列互相关甬数如(4)式。由式(4)知，该映射具有类δ函数的自相关性和零值互相关性，与白噪声性质类似，随机性能好，因而可以作为密钥应用于数据通信或多媒体安全领域。

2、一维无限折叠映射

一维无限折叠映射的离散化形式可以表示成：

xn ∈(0，b)，a ∈(1，+∞），b ∈(0，1)，n=1，2，…，N，该映射系统是一维Markov系统，在区间内有可列个非线性分段、第一类不连续点和不稳定不动点。

该序列具有正的李氏常数，凶而是混沌的，且其值随d增大或6减小而增大，当d越大，b越小时，其值远远大于Logistic映射李氏常数In2，系统变得更加复杂，初值敏感性更强，信息扩散的速度更快，当b→0，a→∞时，趋近于均匀分布，较Logistic映射随机性好，文中参数选取a=10，b=0.99。

3、Lorenz映射

Lorenz映射是由美国麻省理工学院的气象学家洛伦兹在1963年研究大气运动时描述的：

Lorenz映射是一种维数较高的连续混沌系统，其分形维数介于2~3之间，且主要由参数r决定。可以用数值积分的方法求得，如采用四阶龙格一库塔法对方程进行数值积分，得到随机性较好的连续数值序列，xn，yn，zn可以选取任一序列作为混沌映射序列，并从中随机抽取b个数据，对选取的数据做取整处理。得到的随机自然数作为猫映射矩阵系数。文中参数选择t=10，b=8/3，r=28。

4、猫映射

猫映射最早由Arnold引入n，其二维映射形式可以表示为：

定义矩阵，行列式c的值为1，即该映射是一个二维保面积、可逆映射，没有吸引子。实际上，猫映射包括拉伸和折叠两个过程，乘以矩阵C，使x，y变大，相当于拉伸，取模使x，y又折回单位矩阵内，相当于折叠，矩阵C的特征值；相应的李氏常数，因此该系统是混沌的。现在，我们将2-D猫映射推广到3-D。引入两个控制参数a，b。

二维映射可以表示成：

将映射扩展到三维平面，首先固定zn，在x-y平面上做二维猫映射：

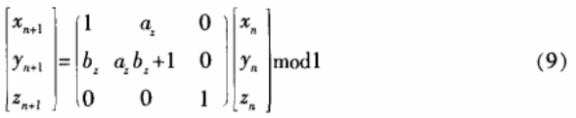
  接下来xn保持不变，在y-z平面上做二维猫映射：

然后yn保持不变，在x-z平面上做二维猫映射：

连接以上三个方程式，则：

其中：

其中：

a2=0.243 (k1，a3=0.572 8<1，远远大于二维映射的特征值，相应的最大李氏常数Ai=ln7.184 2>0．因而三维映射系统变得更加复杂。变换后A的行列式恒等于1，仍为l-I映射，具有保体积性，且存在着逆映射。

二、加密算法

1、移位置换算法

置换本质上是原始图像与加密图像之间对应点处灰度值的移动。移位置换的思想就是通过改变像素的位置即重排像素的位置来达到置乱的目的，使秘文块看起来是随机的。置换操作可以是局部的，也可以是全部的。局部变换要达到较好的置乱效果，必须加大置乱块的大小，但对于比较平滑的图像进行加密时，即使增加置乱块的大小，在加密后的图像中电保留了原图像的大部分信息，加密效果不好。因此，往往采用全局加密的方法。幻方置换是一种常用的置换算法，其思想是：对于图像IM*N，给定幻方矩阵S，将I中像素依S按行或列做一一映射，改变像素位置，达到置乱的目的。在传统的加密算法中，这种移位矩阵是事先定义好的，与密钥无关，因而易于受到差分密码分析的攻击，保密性能较差。本文的置换算法是基于混沌密钥的，移位次数由混沌序列产生，具有一定的随机性，提高了安全性，对图像进行移位置乱后，完成1次加密。

2、灰度值替代

仅仅靠上述移位置换算法，显然保密效果足不够的，要使加密后的图像变得更加随机不可见，就需要改变图像的灰度直方图，即对图像灰度值进行变换。该变换可以在空间域进行，也可以在频域进行，两者各有优缺点。空间域算法简单，计算量小，但置乱效果不是很好；频域算法，需要对像素做变换，计算稍复杂，但经过频域映射，频域内每一点的变化经反变换后，都会对整个数据集合产生一定的影响，加密效果好。随着现代电子工业技术的发展，计算速度已不再成为重要的难题，我们往往更关心的足加密算法的安全性能。因而本文对移位置乱后的图像采用了频域(DCT)变换，利用系数矩阵做比例变换，改变灰度值，完成2次加镪。系数矩阵是由一维无限折叠映射产生，随机性能强，安全性能高。

3、3-D猫映射

一个安全性能较好的加密算法应该同时包括置换、替代和扩散三个过程。以上算法经过了置换、替代两个过程，猫映射则相当于对序列进行扩散。它利用猫映射的拉仲和折叠的性质，使原来相邻的两点，经过迭代映射后，变得不再相邻，具有一定程度的初值敏感性和混沌性。要将猫映射推广至三维，首先应对原图像的灰度矩阵按行或列进行重排操作，变到三维空间，如原图像I，大小MxN，变换后成为（3，mod（MxN/3），即如果MxN不能被3整除，则需要添加0值来补充矩阵，经过猫映射后重排像素值，重新变到二维，并去掉添加点，恢复到原图像大小MxN．完成3次加密。映射矩阵A由高维混沌系统Lorenz产生，它含有3个变量、3个参数，加大了密钥空间，不易被破译。映射系统矩阵采用整数值，由于detA=I，其逆映射系数仍为整数，加密、解密操作简单。

4、符号矩阵

利用Chebyshev映射产生实值序列，通过设定一定的门限值，对实值数列进行变换，转变成符号序列，由于实值序列具有随机性，因而产生的符号序列也具有类似的性质，然后对图像的ix:系数做逐点变换，改变符号，完成4次加密，得到加密图像。

三、混沌序列的生成和加密算法实现

设读人图像I，大小为MxN。

1、迭代次数和系数矩阵的产生

输入密钥（x1，n1，n2），利用一维无限折叠映射产生序列值{Xk}。为了获得均匀性和随机性能更好的序列，去掉前(n1-1)次迭代结果，取Xn1，迭代次数step=round(xn1*10)。我们定义：

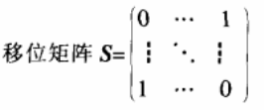
做移位置换，由于I与S是一一对应的，经过step步移位置换，随着S变换为S1，I也变换为I1。去掉前(N2-1)次迭代结果，用xn2作为初始值，生成混沌序列，对序列值进行熏俳，使其与原图像大小匹配，作为系数矩阵y,Y=MxN。

2、猫映射矩阵

输入密钥(xo，yo，zo)，作为Lorenz映射的初始值，利用四阶龙格一库塔法求解，积分区间为[-60，60]，积分步长为0.3，得到序列值{xk}，{yk}，{zk}，任意选取其中一序列生成猫映射矩阵的系数值，如取{xk}。为了减少计算置，我们作必要调整，对数值取整后再做模3运算，使ax，ay，az，bx，by，bz ∈｛0，1，2｝，即：

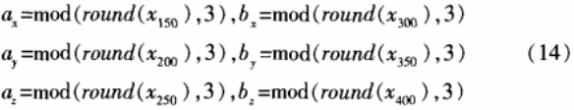
得到猫映射矩阵A。

3、加密算法实现

（1）读入图像IM*N。

（2）输入密钥(x1，n1，n2，x2，n3，xo，yo，zo)。计算移位序列的迭代步数step，符号矩阵S，系数矩阵y，猫变换矩阵A。

（3）对读人像素灰度值矩阵进行移位变换l1=lxstep。

（4）对图像I进行DCT变换ID=DCT(II)。

（5）改变DCer变换系数IDD=ID *Y。

（6）做3-D猫映射I=xIDD。

（7）改变系数符号，点成符号矩阵Ifnd =IC．*sign。

（8）输出加密图像。

4、解密算法实现

解密时，按照上述图像文件加密过程求逆操作即可。

四、实验仿真结果

实验时，我们选取以下密钥对该加密算法进行仿真，即选取n1=1 000，x1=0.207 764，x2=0.607 764，n2=500。n3=500，xo=0.678，y0=0.276.2，z0=0.789。

实验结果如图1-图3所示。从图中可以看到该加密算法可以很好的懈密原图像。此外，我们还绘出图像的灰度直方图，如图4—图6所示。从图中可以看到加密后的图像，其灰度值分布和原图像有很大差别，因而很难从加密图像中获取原图像信息。

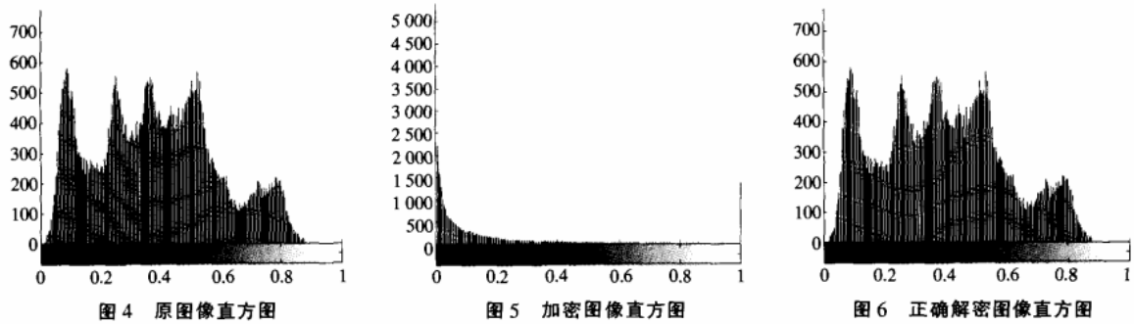
图7—图9分别表示在错误密钥下，懈密的图像。图7为采用错误密钥x:=0.207 764 000 000 1（即对应只有系数矩阵改变）；图8为采用错误密钥X2=0.607 764 000 000 1（即对应只有符号矩阵改变）。图9为采用错误密钥xo=0.678 000 000 000 1（即对应只有猫映射矩阵改变）错误解密后图像。三种情况下，未指明的密钥均保持不变，三种情况密钥误差都很小，达10-13个数量级，从图中可以看到，三种情况均不能正确解密原图像，原图像信息完全丢失，因而该加密算法时非常安全的。

在信息高速流通的时代，不仅要求大量存储和传输图像，而且往往要求在保证质量和安全性的前提下，以较小的空间存储图像和较少的比特率传输图像，即采用图像压缩编码技术。该算法加、解密是在DCT域中进行，因而对于一定的有损压缩图像也可以较好的恢复解密原图像。实验结果如图10—图14所示，采用256x256的灰度图像，压缩比分别为2:1、4:1、8:1时，加密、解密图像，从图中看到该算法可以很好的解密被压缩的图像。

admin普通用户

海报分享