admin 针对传统的网络加密技术中的机密性、真实性、完整性、不可否认性和存取控制等安全问题，从信息安全的基本知识出发，我们通过对PKI技术的学习和研究，开发出一整套基于改进椭圆曲线加密算法的网络加密技术。该方法通过直接计算网络系统中的数据，减少运算时间，具有安全性高、速度快、密钥短、实现时所需占用资源少的特点。
一、网络入侵检测系统中的改进椭圆曲线加密技术
1、椭圆曲线加密算法原理
为了保证人侵检测系统中的安全性，可以运用椭圆曲线加密技术达到目的，首先需要定义参与运算的椭圆曲线。曲线的方法表示：
曲线上所有的点都是非奇异的，这是先验条件。
为了满足普遍性，曲线表示的形状不单单是椭圆，能够包含一些特殊的曲线形式，具体的方法如图1所示。
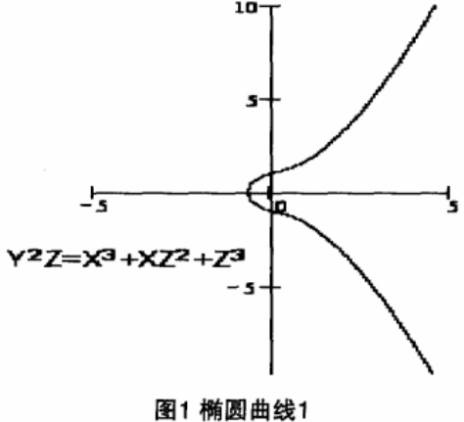
非奇异性需要用数学的方法进行约束，反应到数学曲线上表现为其3个方向上的偏导数结果不能同时等于零，这样能够有效保证所有曲线上的点都为非奇异的。当然也有一些特殊的形式，就是满足曲线方法确不一定能够表示椭圆，如图2所示。
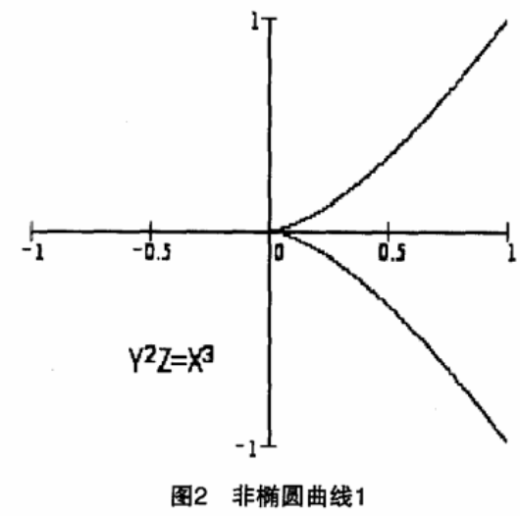运用椭圆曲线进行网络入侵检测的过程，如图3所示。
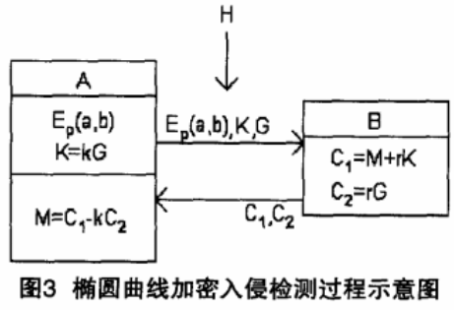
如果有一个偷窥者H，他只能看到Ep(a，b)、K、G、C1、C2而通过K、G求k或通过C2、G求r都是相对困难的。
因此，H无法得到A、B间传送的明文信息，如果想正确描述一个加密椭圆，需要多个变量，设为T=(p，a，b，G，n，h)。(p，a，b）用来确定一条椭圆曲线，G为基点，n为点G的阶，h是椭圆曲线上所有点的个数m与n相除的整数部分)。这是参数的合理选取对加密的效果至关重要。
2、一种改进的快速算法
传统的椭圆曲线加密算法：根据椭圆曲线倍点公式，在有限域GF(q)上，设P=(X,Y)，2P=(X1,Y1)。其中：
在计算的过程中一般要用到2eP，k>=1，可以直接一步步地计算2P，2zp, 23P...，但是这样效率非常低，文献中提出可以直接计算4P，8P，16P来计算2mP，rn>=1，
而不是一步步计算2P，22P，23P…，算出4P=(x2，y2）其中：
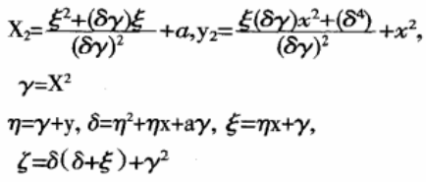
从这些表达式中可以看到，虽然直接计算4P与先算2P辱算2x2P；相比需要多计算9次乘法，但是可以少一次求逆运算，由于一次求逆运算的时间通常多于9次乘法的时间，所以这样能有效地减少运算时间。改进的快速算法：在上面的基础上进行推广，给出直接计算2sP，1<s<=m的公式，可以进一步减少计算量口先推导出2sp，1<s<=m的表达式，记2kp(xp,yp)，则：
这么做能够大幅地缩减加密时间，具有安全性高、速度快、密钥短、实现时所需占用资源少的特点，对网络加密的过程产生了较好的优化作用。
二、实验分析
为了验证本文方法的有效性，进行一次对比实验，实验模拟常规的网络加密过程，对在不同加密算法下的两个加密过程进行统计，查看算法下加密过程的效果和消耗的时间，算法中选用同一套硬件设备，消除硬件带来的延迟，算法的加密过程都以较大程度的176位运算为例，各自的时间如表1所示。
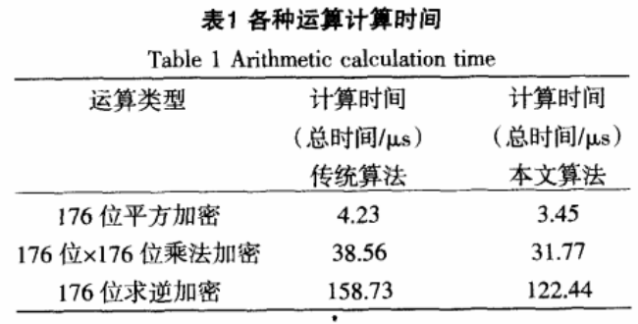
通过以上的统计结果能够看出，在改进后的椭圆曲线加密算法中，网络加密所消耗的时间大幅度的降低，很好地解决了传统方法中的加密耗时，资源开销大的问题。
小知识之椭圆曲线
椭圆曲线指的是由韦尔斯特拉斯（Weierstrass）方程 y2+a1xy+a3y=x3+a2x2+a4x+a6 所确定的平面曲线。若F是一个域，ai ∈F,i=1,2,…,6。满足式1的数偶(x,y)称为F域上的椭圆曲线E的点。F域可以式有理数域，还可以式有限域GF(Pr)。椭圆曲线通常用E表示。除了曲线E的所有点外，尚需加上一个叫做无穷远点的特殊O。
