空域彩色图像混沌加密算法

针对彩色图像的存储特性提出一种混沌加密算法——空域彩色图像混沌加密算法，该图像加密算法首先对Lorenz系统输出的实值混沌序列进行预处理，然后利用其构造置乱索引矩阵，进而实现空域彩色图像三基色置乱，它很好地克服了传统图像文件加密方法秘密不能全部寓于密钥之中的缺陷，被广泛运用。

一、Lorenz混沌序列的预处理

Lorenz系统的动力学方程为：

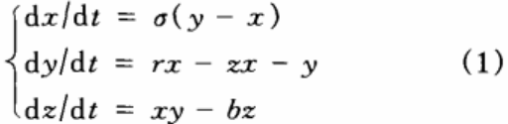
其中，系统参数σ，r，b的典型值分别为σ=10，r=28，b= 8/3。在σ和b保持不变，r>24.74时，系统进入混沌态。该系统输出的实值混沌序列的时域特性如图1 所示（仅以x实值混沌序列为例）。

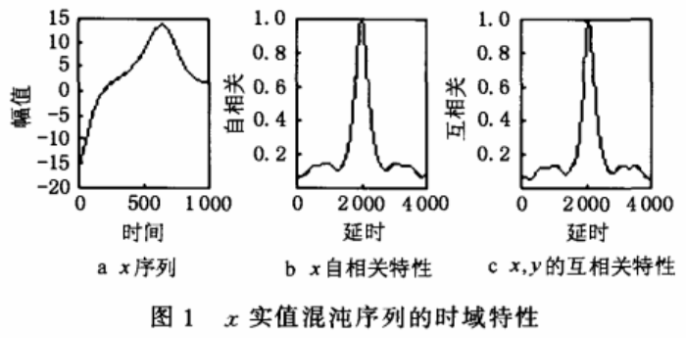
该系统输出的实值混沌序列固有一些缺陷：x，y，z的值域各不相同，不利于批处理；x，y，z局部取值呈现单调性，易受线性预测攻击；x，y，z自相关特性非理想的艿函数，互相关特性非理想的零特性，不仅难以保证不可预测性，而且系统多输出特性也不能得到充分利用，另外，由于系统混沌特性的成熟研究，使其容易被攻击，所以对Lorenz混沌序列的应用必须予以处理，以克服其自身缺陷、充分发挥其三输出的特性，并将其成熟特性加以演变。对于连续混沌系统，改善其混沌序列伪随机特性一个最简单的方法是加大积分步长。但是，随着所需序
列长度的增加，迭代时间也将随之增长，且积分步长的加大并未改变混沌序列的演化规律，通过大量的数据分析，本文构建了对Lorenz混沌序列预处理的数学模型。

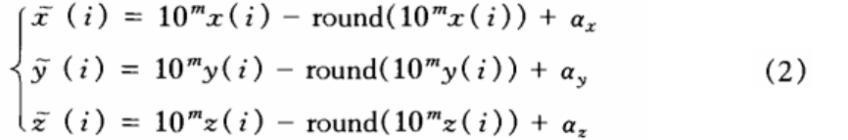
其中，x'，y'，z'为预处理后的实值混沌序列；m为移位控制参数，通过它可以提高序列取值的不规则性；round(．)为取最接近整数运算，对Lorenz系统混沌特性加以不可逆演变；a为转换因子，当a=0.5时，即得到(0.1)分布的实值混沌序列。

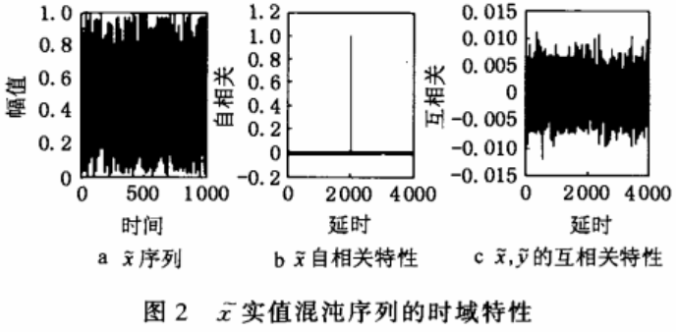
x'，y'，z'实值混沌序列的时域特性如图2所示（仅以x'实值混沌序列为例）。预处理结果为x'，y'，z'的值域均为(0，1)；取值不规则性大大提高；3个实值混沌序列均有较理想的δ函数自相关特性，近似为0的互相兼特性。同时预处理还不可逆地演变了Lorenz系统为人所熟知的混沌特性，进一步提高了算法的保密性。x'，y'，z'可独立使用，也可互相组合构成多个加密混沌序列，实现图像文件的多路并行加密。所有这些均说明预处理是正确、可行的。

二、空域彩色图像混沌加密算法／解密算法

从及iam算法的计算速度、置乱程度、抗攻击能力等因素综合考虑，本文提出以8×8块为单位的彩色图像三基色空域置乱算法，其基本原理如下：

1、 Lorenz系统3个参数和3个初值作为算法的密钥足（σ，r，b，xo，y0，z0）（还可以加入算法设计过程中的部分控制参数）。混沌系统对系统参数和初始状态极其敏感，因此加密算法理论密钥空间无穷大，有着近于“一次一密竹的安全性。

2、置乱算子——置乱索引矩阵，由混沌系统的密钥控制生成，不同的密钥生成不同的置乱算子，其秘密全部寓于密钥之中。因此加密算法符合Kerckhoffs准则，满足现代加密体制的要求。

置乱索引矩阵的构造．由x'，y'，z'实值混沌序列生成索引序列lx，ly，lz，用其构造置乱索引矩阵Px，Py，Pz。索引序列指定置乱索引矩阵中各元素的几何位置，各元素按索引序列的顺序赋以0，…，l的自然数，则置乱索引矩阵的任一元素Pi∈[1，2，…，n]，且Pij=Pkl，当且仅当i=j，k=l。

3、将待加密彩色图像的R，G，B3个分量按8×8大小分块，以块为单位分别用置乱索引矩阵Px，Py，Pz进行空域置乱。JPEG压缩过程的二维DCT、系数量化以及熵编码都是以8×8块为基本单位进行的，图像像素几何位置被置乱，破坏了DCT系数的分布概率；而Huffman编码表无法按最优方式使用，导致压缩后解密效果变坏。按8×8块置乱大大地减小了对DCT系数分布的破坏，使加密图像对JPEG压缩具有一定的抵抗能力；同时其既不失全局置乱的优势（尤其对大尺寸图像），又能降低计算强度和空间需求。

加密算法

Step1、输入待加密彩色图像文件。分离彩色图像的R，G，B三基色分量。

Step2、Lorenz混沌序列预处理．输入密钥是(σ，r，b，xo，y0，z0）。生成x，y，z实值混沌序列，应用式(2)对x，y，z混沌序列进行预处理，得到x，y，z实值混沌序列。

Step3、构造置乱索引矩阵．按需要长度l=(M×N)/(8×8)随机截取x'，y'，z'，升序排列[a，lx]=sort(i)，[b，ly]= sort(歹)，[clz]=sort（y'）；用生成的索引序列lx，ly，lz按行或列转换成二维矩阵，即得置乱索引矩阵Px，Py，Pz。

Step4、空域置乱．按置乱索引矩阵Px，Py，Pz规则重排三基色分量8×8块的几何位置，实现块式空域置乱。

Step5、输出置乱彩色图像文件。合成R，G，B三基色图，即得置乱彩色图像文件。

解密算法是加密算法的逆过程。

三、仿真实验

1、密钥空间的保证

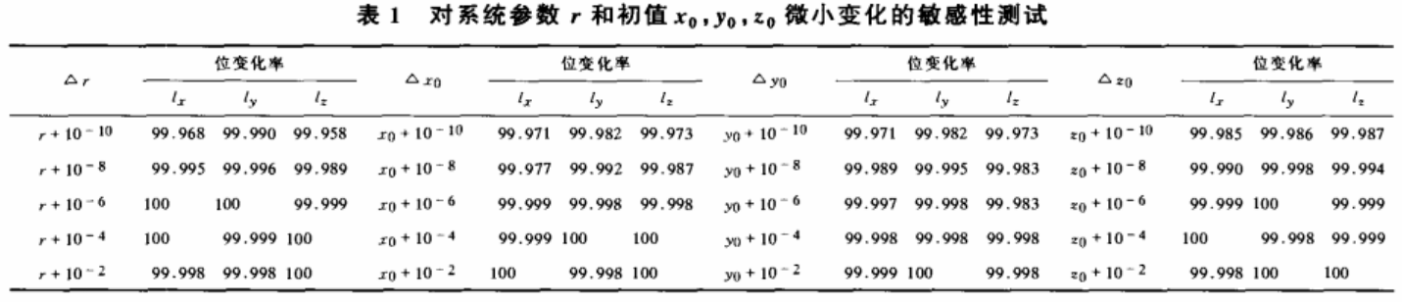
测试条件如下：系统参数σ=10，r=28，b=8/3；初始值xo=0.1826059374，yo=0.3627091485，zo=0.2519407368；迭代次数以=1×105（除去了序列的初始段）。系统参数r和初值x0，yo，z0分别发生微小变化。测试结果如表1所示，其中的位变化率指索引序列的位变化率，当系统参数和初值发生微小变化时，索引序列的位变化率超过99%。这表明预处理后的混沌序列仍对系统参数和初值极其敏感，既保证了算法的密钥空间，同时说明若采用有微小错误的密钥尝试解密是不可能的，且算法能够抵抗对密钥的穷举攻击。

2、保密性测试

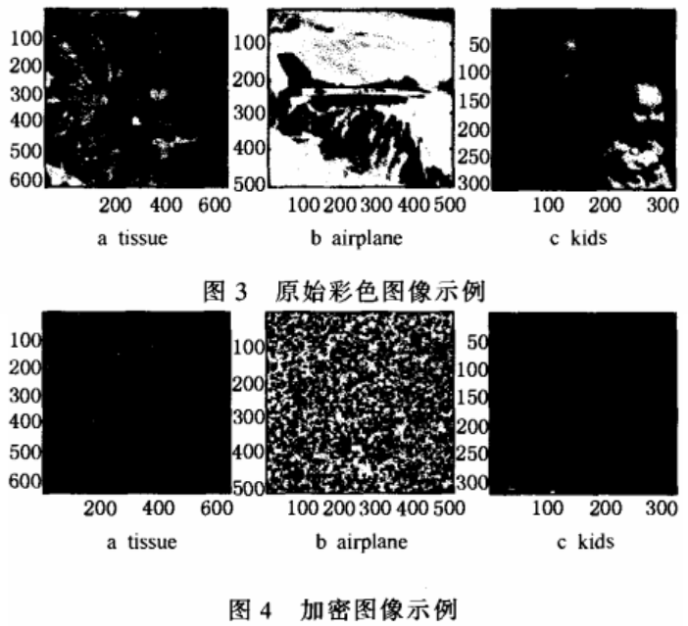
如图3所示，选择640×640tissue，512×512 airplane，320×320 kids 3幅具有不同纹理特征的标准图像；图4所示为置乱图像。从密码学角度，为了加强算法的扩散过程，三基色分量
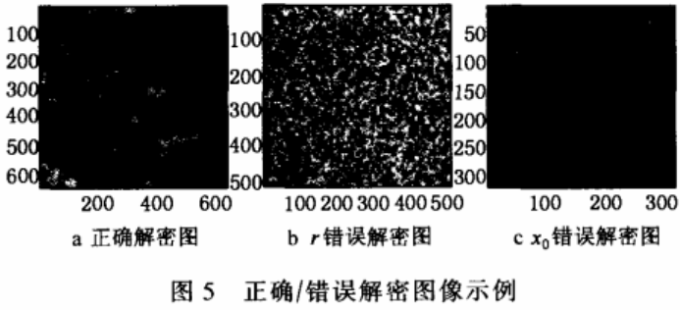
分别用Px，Py，Pz置乱。若采取唯密文攻击，则解密工作量高达3×(M×N)!，迸一步加大了破译难度，另外，三基色分量分别置乱，混淆了彩色图像文件每一像素的R，G，B三元素，使加密图像文件在视觉上发生了色彩变化，图像更难读懂。图5所示为正确解密和错误解密示例，其中图5a所示为以tissue为例的正确解密图像，图5b所示为以airplane为例，参数r的偏差为10 -10时的错误解密图像，图5c所示为以kids为例，初值x0的偏差为有10 -10时的错误解密错误解密示例，其中图5a所示为以tissue为例的正确解密图像，图5b所示为以airplane为例，参数r的偏差为10-10时的错误解密图像，图5c所示为以kids为例，初值zo的偏差为有10 -10时的错误解密图像，由于x，y，z实值混沌序列对系统参数和初值极其敏感，即使密钥有微小变化也会得到完全不同的置乱索引矩阵，从而导致错误的解密结果。

3、置乱度分析

常用于图像失真度量的峰值信噪比和归一化互相关度不能很好地刻画图像的置乱度，怎样对置乱效果进行量化，以客观地反映置乱算法的有效性。给出了图像置乱程度的3个定义，但其不便于计算，张华熊等利用概率论中的均值和方差定义以阶置乱度的计算公式，计算较为复杂，本文引入了一种以最简单、最常用的Arnold置乱作为基底的置乱度量，可以用来衡量对混沌置乱的置信度，其计算式构造为：

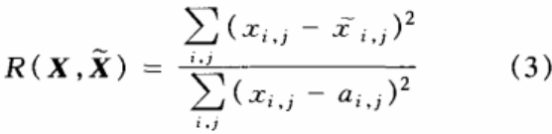
其中，X={xi,j }N表示原始图像，X'={x'i,j }N表示混沌置乱图像，A={xi,j }N是Arnold置乱图像。二维Arnold变换为：

其中x，y∈(0，1，2，…，N-1)为某一像素点的原坐标，x’，y'∈(0，1，2，…，N-1)为变换后的坐标，N是原始图像矩阵的阶数。Arnold变换具有周期性，对应给定的自然数N≥2，Arnold变换的周期是使得：

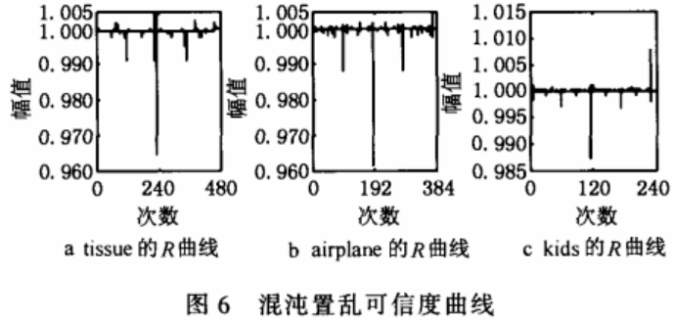
成立的最小自然数n，则对应640×640图像文件，n=480；对应512×5 12图像，n=384；对应320×320图像，n= 240。

图6所示为对图3中的3幅图像进行置乱并应用式(3)计算出的对应Arnold变换一个周期的置乱度曲线。可见，本文的混沌置乱与Arnold变换相比不低于96%，具有一定的可靠性。

4、抗攻击测试

图7所示为加密图像受到压缩处理、噪声污染及几何失真后的解密效果，图7a所示为以tissue为例的图像文件加密经约20%不规则剪切后的解密图像，其与原始图像的相似度为86.2396；图7b所示为以airplane为例的加密图像经75%的JPEG压缩后的解密图像，其与原始图像的相似度为92. 6496；图7c所示为以kids为例的加密图像受到10%强度的高斯噪声污染后的解密图像，其与原始图像的相似度为84.53%。

admin普通用户

海报分享