将混沌映射应用于加密和解密,产生的加密算法比现有的加密算法实现方便,加密和解密速度快,安全性高,使得近年来混沌加密的研究成为加密研究领域的一个热点。那么,我今天就给大家介绍一种基于一维离散混沌映射的图像加密算法。
一、基于一维离散混沌映射的图像加密算法
该加密算珐的结构类似于Feistel网络结构中的SP网络结构,分为替代变换和置换变换两部分,用于给图像文件加密,图像为N×N的矩阵,I(i,j)为图像(i,j)点的像素值,L为图像的灰度级数。先对像素值I(i,j)进行替代变换,再对位置点(i,j)进行置换变换,迭代r轮后进行加解密。
其中替代变换算法如下:

加密过程,首先由混沌映射式(2)产生一个伪随机序列Xn,经过式(4)处理为一致分布的混沌序列,再经过式(5)转化为整数赋值给K(i,j),最后由式(1)将像素值替代。其中,η>1且不大,密钥为(x0,η)。
置换变换算法如下:

置换变换将像素从位置点(i,j)移位到(S1,S2),r为迭代的轮数,密钥为(ki,o,k2,0,a,b)。算法流程如图1所示。
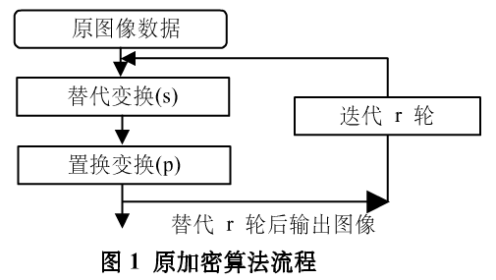
二、对基于一维离散混沌映射的图像加密算法的分析
首先,分析该算法的置换变换,将置换变换中的式(8)和式(9)分别代入式(6)和式(7),得
![]()
由此可见,每一轮后,新位置点的一维顺序mi都可以表不成i,j和k i,j的固定函数:
![]()
其中p,p'为只含i,j变量的表达式且modN的函数,q,q’为只含kn1、n2变量且modN的函数。
由式(14)可知迭代r轮后,新位置点的位置由q(kn1、n2)与q’(kn1、n2)确定,q(kn1、n2)与q’(kn1、n2)所有的不同值只有N×N个,即新位置点的不同种类也只有N×N个,而不是随机变换应有(N×N)!个。N×N是很小的一个数,使用穷举方法,几分钟就可找到正确的新位置点的位置。该加密算法的置换变换所提供的密钥空间太小,不能保证数据的安全性。
再分析替代变换算法,在加密算法中,该文作者使用了称之为“完全不可预测”的离散混沌映射式(2),该文认为该序列的下一个值不能由序列的以前值预测,并举例:
η= 3/2,xn,xn+1可表示为:
![]()
-1<t<1,若想从Xn计算Xn+1则有两种可能:
![]()
因此从当前值不能预测下一个值。但该例只能证明当密码攻击者掌握的序列值不够多时,无法预测序列值。而当密码攻击者掌握的序列值足够多时完全可以求得式(2)中的θ与η。比如该例中,若密码攻击者知道从第n项开始的若干个序列值,则由式(2)知:
![]()
由于θπηn为一有限值,则式(18)的解集的个数有限,再由式(17)知对式(18)的解集,xn+1有两种可能,则加入xn+1的方程,解集的个数成倍减小,继续加入序列值,可以求出唯一的θ与η值(见表1)。
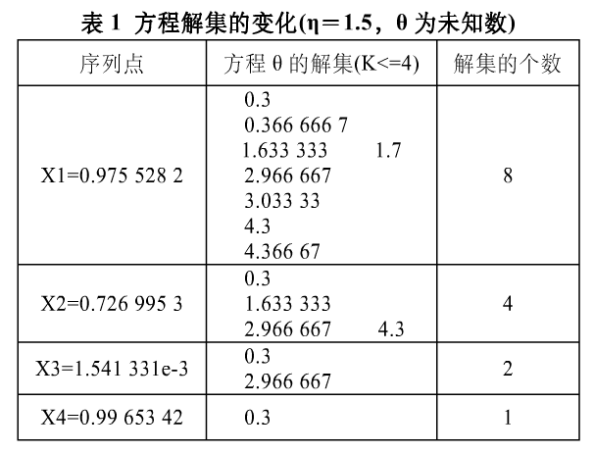
更糟糕的是,当密码攻击者掌握了序列的前3个点时,由于θ值<1/2,η不大,则仅3个点就可求出θ与η(由于图像文件的格式标志处于文件头,这部分的明文容易猜出)。可见使用该一维离散混沌映射的替代算法也不安全。
又由式(1)知,由明密文对可推知k(i,j),再由式(5)知,yn约等于k(i,j)/(L-1)(当L很大时,比如对于L=232+1,并且数据使用单精度,则二者没有误差;而当L比较小时,可求密钥的前若干数位的值),又由式(4)可求得xn。由此可知由明密文对可推算出该一维离散混沌映射值(见式(1 9))。
![]()
将式(2)和式(4)代入式(19)得:
![]()
其中mi为该点在i轮时的顺序。式(20)可化简为式(21)。
![]()
int()为求整函数。将式(14)展开:
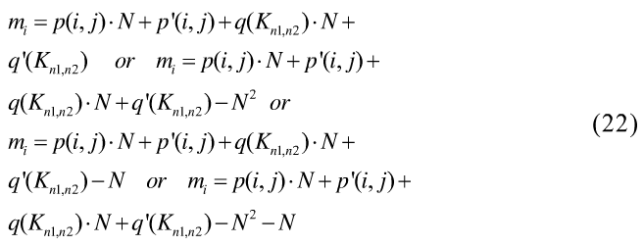
设q(kni,n2)×N+q’(kni,n2)为T i,则每一轮的顺序可由一个变量决定点的位置。
综合以上分析,对该加密算法可提出完整的已知明文攻击方法:
(1)对已知明文穷举N×N种密文位置,获得明密文对。
(2)每一个明密文对,推算出式(20)的右边的值(设为ai)。
(3)每一个明密文对,对应一个方程,由所有的明密文对列出如式(21)的方程组。该方程组有r+1个未知数,则需要有r+1个明密文对,由于式(10)和式(11)的关系,未知数的个数不会随r的变化而增加,理想的情况下仅需6个方程就可求出任意r轮的密钥。
(4)使用牛顿迭代法或其它方法解此非线性方程组,求出Ti和θ,η。
(5)用解得的密钥解密图像,直到得到正确图像为止(见图2)。
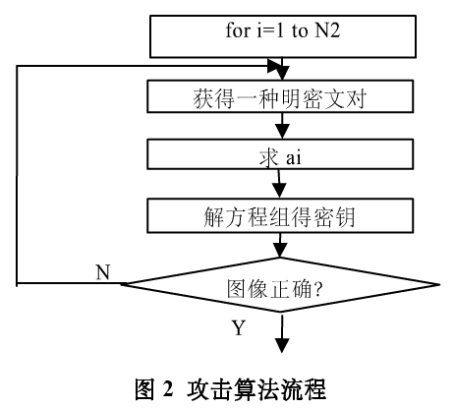
三、基于一维离散混沌映射的图像加密算法攻击实例
设r=2, 0=0.223 456 7,η=1.ooi 432, ti=1(k1,i=0,k2. 1=1),N=256,L=232+1,并且数据使用单精度,将图像pepper加密,如图3(a)所示。已知图像点(0,0),点(0,1),点(1,0)的像素值,穷举65 536种密文位置后,由其中一种正确的明密文对推算出ai=1.107 688 8,a2=1.548 374 6,a3=1.978 115 1(ai,a2,a3还可能等于0.107 688 8,0.548 374 6,0.978 115 1但获得的解不能解密图像)。列出的方程组如下:
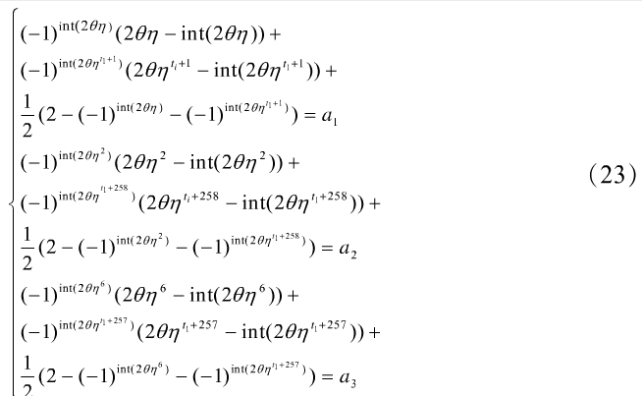
使用牛顿迭代法,θ初值为0.22,η初值为1.001,t1初值为0,int(x)的导数为0。求得结果为θ=0.223 456 7,r1= 1.025432,t1=1,破译的结果如图3(b)所示。结果完全正确,说明该加密算法分析的攻击方法有效。

四、基于一维离散混沌映射的图像加密算法建议改进方案
基于一维离散混沌映射的图像加密算法的存在以下安全漏洞:
(1)替代算法的混沌加密不能抵御已知明文攻击;
(2)替换算法的混沌替换只提供了很小的密钥空间,不能抵抗穷举攻击。
本文建议修改其替代变换算法和置换变换算法,首先使用分段线性映射式(24)经过多次迭代前馈的一维离散混沌算法来代替式(2)的算法。
![]()
使用式(24)时,采用多次迭代进行前馈,即Xn+i=Fm(xn),迭代的次数m如果大于数据的实现精度,则可抵御已知明文攻击。事实上,即使攻击者知道多个经过m次迭代的混沌序列值,由于Xn+1与Xn之间可能的分段种类有4m种,比穷举密钥的次数还多,又任意Xn+l与Xn之间的分段都不同,lyapunov指数也求不出来,因此已知明文攻击无效。其次本文建议将置换算法进行如下修改:每轮迭代替换之前,由式(11)产生一个不同的混沌序列数,将其作为式(10)的初始值,由式(10)产生N2个混沌序列数,将这N2个不相等的混沌序列数由小到大排序,序列的原顺序与排序后顺序形成的一对一映射作为置换变换。新的置换变换的种类有(N2)!个,穷举攻击完全无效。经过如上修改,该加密算法的安全性得到很大提高。
小知识之Lyapunov指数
Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。对于系统是否存在动力学混沌, 可以从最大Lyapunov指数是否大于零非常直观的判断出来: 一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。










