基于高维广义猫映射的图像加密算法就是将三维广义猫映射扩展至四维广义猫映射,通过将图像的像素坐标和灰度值作为广义猫映射的初始值,映射参数和迭代次数作为密钥实现图像文件加密。与常见的低维混沌猫映射加密算法相比,该加密算法具有更大的密钥空间及更高的加密速度,可作为加密系统的一个子模块用于常规网络或中高速无线传感器网络图像、数据块和视频的加密传榆。
一、从二维猫映射比较密码变换与混沌映射的关系
猫映射(Cat map)最早是由Arnold引入的,因为经常用一张猫脸的图进行演示而得名,其方程如下:
![]()
式中,xn,yn都是实数且满足0<xn,yn<1(n=0,1,2,…)。(xn,yn)的相空间被限制在单位正方形[0,1]×[0,1]内,猫映射在此正方形内不断地进行线性的拉伸(乘以矩阵使xn,yn都变大),然后折叠(通过取模使xn,yn又折回单位正方形内),具有Shannon在其经典论文《保密通信理论》中指出的一个好的混合变换应具有的“在有限区域内进行反复折叠、拉伸变换的特性”。
将原始的猫映射定义(1)式数字化,即xn,yn(n=0,1,2,…)均取正整数而非任意实数,得到如下二维广义猫映射:
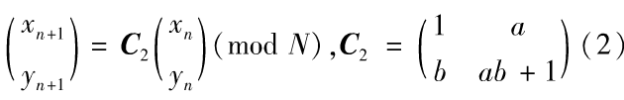
式中a,b,N为正整数。可以证明(2)的参数a,b以N为周期,故要求a,b∈N。若初始值x0,yo为正整数,则xn,yn(n =O,1,2,…)也均为正整数,数字化后的猫映射(2)仍然具有猫映射的拉伸和折叠的性质,故可通过将图像的像素坐标及灰度值作为(2)的初始值进行迭代来实现图像的加密。对于图像内原来相邻的两点如(xn,yn)和(xn,yn+1),其像素坐标经广义猫映射迭代几次后不再相邻;具有均匀概率分布的猫映射还可以保证经过一定次数的灰度值迭代后,原加密图的灰度直方图由具有特定的统计规律改变为呈均匀分布,从而达到图像保密的目的。
二、从二维广义猫映射到高维广义猫映射的扩展
本节给出三维广义猫映射的定义并将其扩展至四维广义猫映射。基于三维到四维的扩展模式可以将广义猫映射扩展至更高维如八维,但由于篇幅限制及基于表述简介的原则,下面以四维广义猫映射为例说明如何将低维猫映射扩展至高维广义猫映射。
1、三维广义猫映射
将二维广义猫映射(2)扩展为三维广义猫映射:

其中N为正整数,ai,bi(i=x,y,z)∈N且为正整数。
2、四维广义猫映射
通过以下4个映射子变换可以实现从三维广义猫映射(3)到四维广义猫映射的扩展。在(x,y,z)三维空间进行三维广义猫映射,同时令,γn+1=γn由(3)可得:

在(x,y,γ)三维空间进行三维广义猫映射,同时令zn+1=zn,由(3)可得:
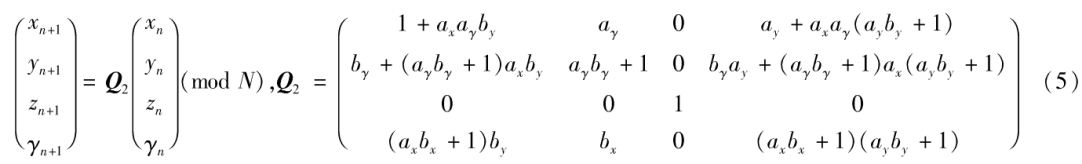
在(x,z,γ)三维空间进行三维广义猫映射,同时令yn+1=yn由(3)可得:

在(y,z,γ)三维空间进行三维广义猫映射,同时令xn+1=xn由(3)可得:
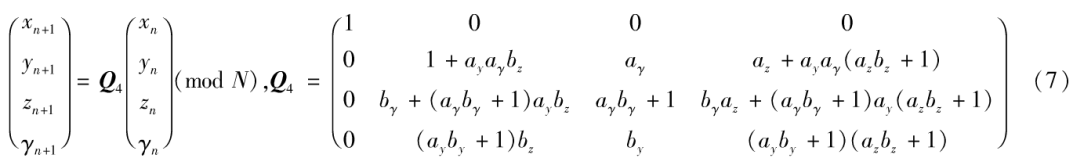
联合(4)~(7)可得四维广义猫映射为:
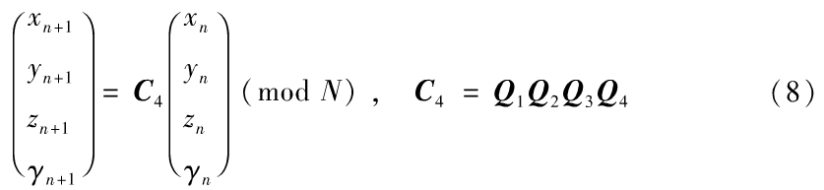
为计算及表述简洁起见,可令各基本参数ax=ay=az=aγ=bx=by=bz=bγ=1,有:

上述各维广义猫映射均为保面积的,即满足:
![]()
3、三类广义猫映射的基本动力学特征
选择一个合适的基本混沌映射系统,可以减少加密复杂度及提高加密速度且不失去良好的安全加密性能。
根据混沌动力学理论,从刻画动力系统对初始条件敏感性强弱程度的Lyapunov指数和混沌映射分布的均匀性两个方面出发,指出一个合适的混沌映射系统应该具有以下特征:
(1)大的Lyapunov指数
具有较大Lyapunov指数的混沌映射对初始值更敏感,也就越适合用于加密系统。
(2)均匀的概率分布
由于混沌映射的拓扑传递性,一个离散混沌映射的迭代轨迹会落在相空间的每一点的小邻域,但其分布并非一定均匀。具有均匀概率分布的混沌映射可以保证明文经过一定次数的迭代后获得均匀分布的密文,具有较强的抗统计攻击性能。
例如针对Logistic映射的分布在区域(0,1)两端呈现奇异性,基于概率原理的变换方法,实现把Logistic映射产生的非均匀分布随机变量转化为均匀分布的随机变量,进而满足图像置乱需要。与Logistic映射相比,即使是二维猫映射也能保证明文只通过一轮的扩散变换就可获得较均匀分布的密文,这是由混沌系统自身的特性所决定。
由三类广义猫映射的定义式(2)、(3)及(8)可以计算出当各基本参数均取1时,各类猫映射的特征值及最大Lyapunov指数,如表1所示。由表1可以得到,四维广义猫映射的最大Lyapunov指数远大于二维或三维猫映射的最大Lyapunov指数,因此从动态系统对初始条件敏感性强弱程度而言,四维广义猫映射较低维的猫映射更适合加密系统。

三、基于四维广义猫映射的图像加密算法
置换和替代是加密技术的两个基本构造模块。由于对图像像素坐标进行的像素置乱不会改变图像的统计直方图,为了避免统计攻击,通常图像加密算法会引人图像像素值的扩散变换使密文的直方图变得比较均匀,并通过置乱变换与扩散变换的组合进行多轮的变换,以获得更好的图像文件加密效果。
1、图像扩散
欲将四维猫映射应用于图像扩散,可将原始图像分解成2x2的小方块,对每个方块中的四个像素值f(i,j),f(i+1,j),f(i+1,1)及f(i+1,j+1)运用如下变换:
![]()
式中X=[f(i,j)f(i,j+1)f(i+1,j)f(i +1,j+1)]T为小方块中四个像素值组成的向量,X'=[f’(i,j) f'(i,j+1) f'(i+,j) f’(i+1,j+1)]T为经扩散变换后的像素值向量。
2、加密算法
1)设置加密密钥:加密轮数五,猫映射的参数ai,bi(i=x,y,z,γ)∈N;
2)利用二维猫映射式(2)对图像像素的位置进行置乱变换;
3)在每一次的置乱变换后根据式(10)进行基于四维猫映射的像素值扩散变换;
4)转到步骤2),将加密算法中的2)、3)步循环做k轮。
3、解密算法
解密算法是加密算法的逆过程,具体过程如下:
1)设置解密密钥:即解密轮数为忌,猫映射的参数ai,bi(i=x,y,z,γ)∈N与加密时完全相同;
2)进行一次像素值反扩散变换,即运用反扩散的公式:
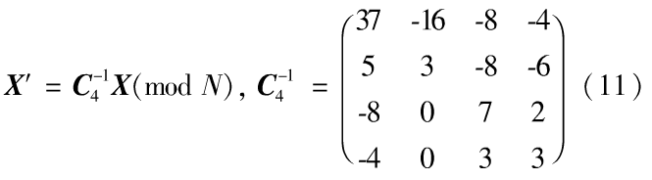
3)在一次反扩散变换后进行像素位置反置乱变换,即运用反置乱变换公式:
![]()
4)转到步骤2),将解密算法中的2)、3)步循环做K轮。
图1给出了对一幅256×256像素经典Lena图像的基于上述加解密算法的加密、解密仿真计算结果(k=3)。

图2给出了原始图像及加密后图像的灰度直方图。

由图2可知,经三轮加密后的直方图(b)呈均匀分布,它掩盖了原始图像灰度直方图(a)的分布规律,用此方法加密后的密文对密钥的贡献很小。
4、加密算法速度与安全性分析
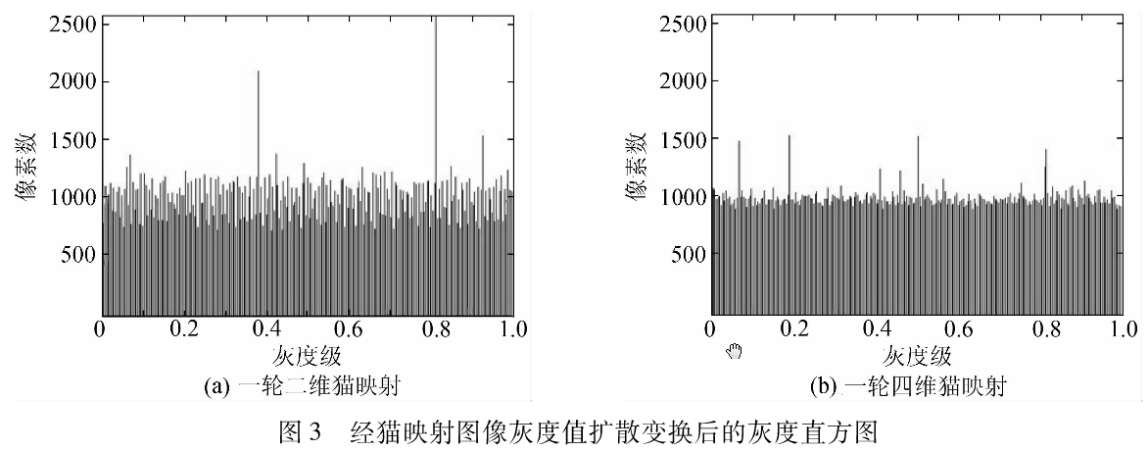
仅考虑单轮计算量时,基于低维和高维的广义猫映射图像加密算法速度无实质区别,两者所需计算时间均取决于原始图像像素的大小,但高维广义猫映射具有更大的Lyapunov指数,这使得基于高维广义猫映射的图像加密算法只需较少的加密轮数即可获得均匀分布的密文,进而可获得更高的加密速度。图3给出了原始图像经过一轮由(2)式描述的二维广义猫映射(a,b均取1)及一轮由(9)式描述的四维猫映射扩散变换后获得的图像灰度直方图。
从图3可以看到,在相同加密轮数时四维猫映射加密算法较二维猫映射加密算法获得了更为均匀分布的密文,表明基于高维广义猫映射的图像加密算法只需较少的加密轮数即可获得均匀分布的密文。
Shannon曾指出理论上不可破译的密码系统是“一次一密钥”系统,主要阐述了在加密过程中每一个密钥仅使用一次的设想。尽管这种“一次一密钥”系统只是一种理想的极限情况,在实际应用中很难实现,但在密码学领域依然是密码算法设计者应遵从的一个指导思想。常见的基于单参数的混沌信号加密,其参数一般固定不变,不符合Shannon提出“一次一密钥”加密系统的设计理念,也是安全性能得不到保证的原因之一。通过分析该图像加密算法的有效密钥量达不到预期的目标,在已知图像攻击下是不安全的。
如果将混沌系统中的某一组便于调节的参数视为密钥,每加密一次就改变这组参数一次,则符合“一次一密钥”的设计思想。本文提出的高维广义猫映射图像加密算法在单独应用时虽然较低维猫映射具有更大的密钥空间,其安全性能并无实质性改善,但可以作为加密系统的一个子模块用于对多帧图像分时并随机地共用某一组切换参数来实现图像或视频的加密。虽然由于不受限的图像帧数将远大于有限的可选切换参数的数量而不能真正实现对每一帧图像的“一次一密钥”加密,但与固定参数的混沌视频图像文件加密相比,其安全性能将得到很大的提高。
小知识之Lyapunov指数
Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。对于系统是否存在动力学混沌,可以从最大Lyapunov指数是否大于零非常直观的判断出来: 一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。











