由于混沌密码分析的不断进步,且已存在的混沌加密算法都或多或少的存在着安全方面的隐患,为此我们需进一步提出新的混沌加密算法,使其可以避免在已有算法中存在的弱点,并且可以抵抗可能性的攻击。基于混沌动态搜索的数字图像加密算法应运而生,这种加密算法将两个Logistic映射与动态查找表相结合,安全性高,加密速度更快。
一、Logistic混沌映射
本文选用Logistic映射产生伪随机序列,其原因在于它对初值的敏感性,以及经过若干次的迭代之后,它产生的数值序列变得毫不相关,并且不可预测。
Logistic映射为:
![]()
当3.5699456....≤u≤4,Logistic映射进入混沌态。即由初始值xo在Logistic映射的迭代下所产生的序列{xi}是非周期的,不收敛的并对初始值也非常敏感。当u=4时,由式(1)所产生
的混沌序列其统计特性与白噪声有许多相似之处,是理想的密码流序列。由于单一的Logistic映射,在被盖化处理之后,周期比较短。因此本文选取2个Logistic映射,一个作为加密序列,另一个作为干扰源,达到扰动,扩大其周期,同时将上一个密文作为反馈放到密码系统中去,以及不断的调整查找表,有效的克服各种攻击。
二、动态查找表
Baptista提出的查找表算法,主要的缺点就是密文分布不均匀,其中很重要的一个原因就是查找表是静态的。本文提出了利用动态查找表的方法有效的克服上述缺点。所谓动态的查找表就是在加密过程中不断的动态的改变表中项的内容,具体形式如图1所示。
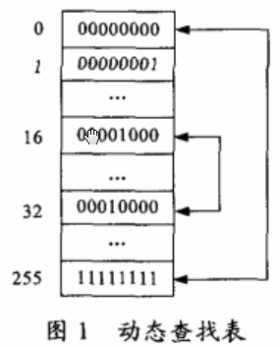
例如,混沌系统输出一个数值为16(经过量化之后),序号16所对应的表项为table[16],按照一个规则将表项中的ASCII码值和另外一个表项交换。具体的交换规则如下:
Table [16]表项值为00001000,将表项值反向输出为00010000,十进制值为32,将table[16]和table[32]中的值进行交换,同时将相邻的4个表项table[14],table[15],table[17]和table[18]按照如上的规则进行交换。若交换的时候发现交换项是本身,例如255(111111111),则反向输出也是其本身,就将起各项取反,即00000000,也就是将table[255]和table[0]交换。
三、基于混沌动态搜索的数字图像加密算法描述
图2给出了本加密算法的加密流程,其具体步骤描述如下:
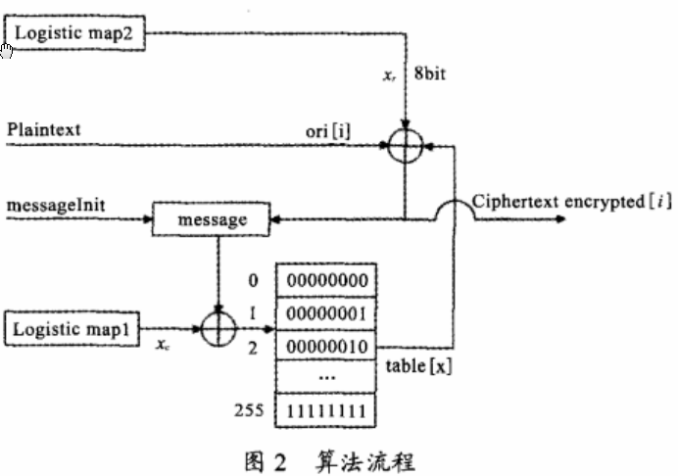
(1)确定Logistic混沌映射1和2的控制参数u1和u2,以及系统初值x1和x2:取u1、u2∈[3.9999997,4],x1、x2∈(0,1),这样映射1和2产生两个混沌序列Xi1,Xi2。
(2)设定message的初值messagelnit,message作为反馈来使用,设置message的一个初值,以后就用密文来代替。
(3)加密时,首先将logistic映射1产生的序列值,按如下规则:
![]()
转化到0-255之间;然后将xi与message相异或得到xe,找到对应的动态表项table[xc]。
(4)将logistic映射2产生的序列值,按如下规则:
![]()
转化到0-255之间;将明文字节org[i]、而xr、table[xc]相互异或得到密文encrypted[i]。特别当Xn>0.5时,按照上述方法进行查找表的动态交换;Xi1≤0.5时,查找表不变化,这样有利于加快加密的速度。
(5)重复步骤(3)、(4),直到穷尽所有明文。
四、基于混沌动态搜索的数字图像加密算法安全性分析
试验环境为:CPU: PentiumIV l.4G;内存:512M;操作系统:Windows XP下,用CH编写代码。选取两混沌映射初值分别为x1=0.245243和x2=0.9345242,系统控制参数分别为u1=4.0和u2=3.992923,messageinit值为50,对应的二进制数为00110010。图3给出了对Lena图像文件加密的效果,其中图3(a)为Lena原图,图3(b)为对应的密文图像。

1、密钥分析
(1)密钥空间分析
两个Logistic映射的初值可取0-1之间的任意实值,两个系统的参数在3.999997-4之间,同时messageinit都可以作为该加密系统的密钥,可见本加密算法的密钥空间较大,不容易破解。
(2)敏感性测试
改变本算法中第2个Logistic映射的初值,如将其增加0.000000001,再对Lena原图文件加密,结果如图3(c)所示。计算图3(b)和3(c)的像素变化率(NPCR)......,其
值为0.46%,这表明密文图像3(b)和3(c)的相似度是非常小的。
2、统计分析
(1)直方图分析
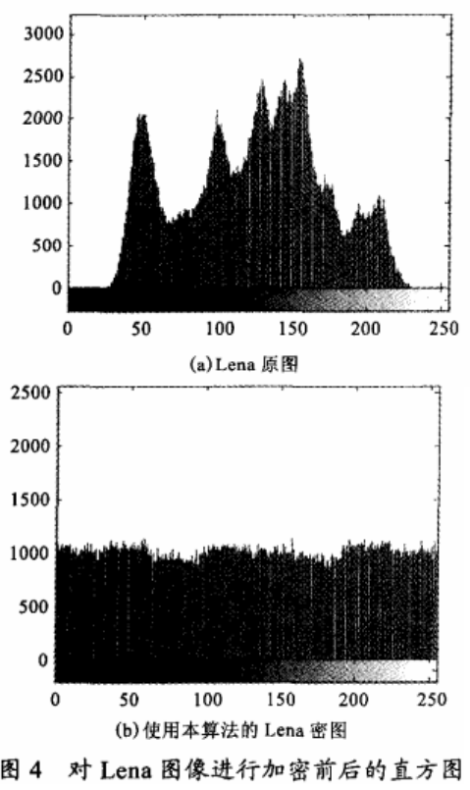
图4为对Lena图像文件加密前后的直方图。图4(a)和图4(b)比较,可见使用本加密算法所得的Lena密图的直方图呈分布很均匀,完全掩盖了变换前的分布规律,才能破译难度进一步增加。
(2)相邻像素的相关性
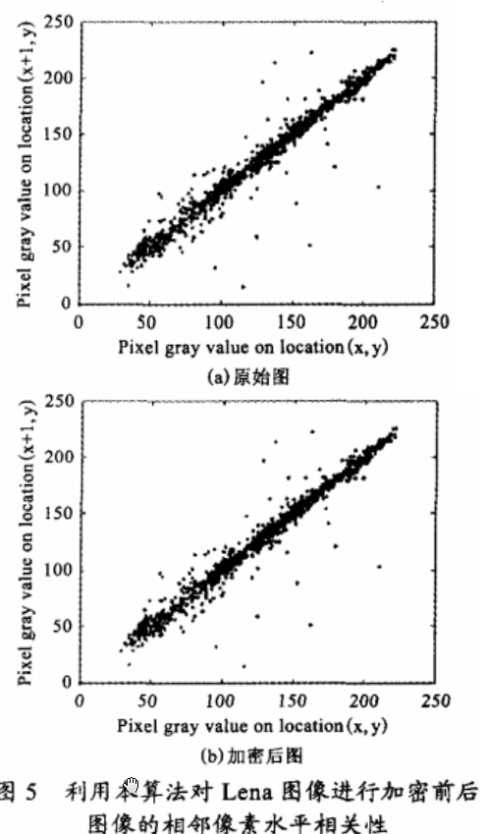
加密前图像中相邻像素的相关性是明显很大,降低相邻两个像素的相关性才能破坏统计攻击.所以在原始图像和加密图像中各随机选1000对像素对,测试其相关性(垂直方向、水平方向),并进行相关系数计算。其中x,y表示像素灰度(两个相邻)。在测试中,使用如下3个离散化公式:
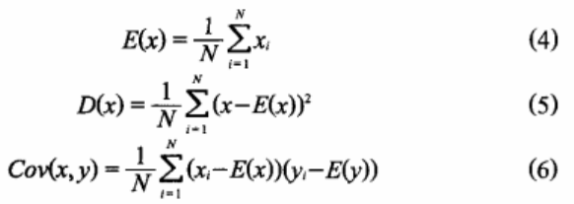
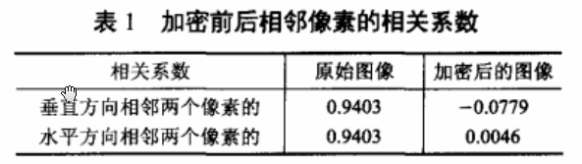
图5给出了利用本加密算法对Lena图像文件加密前后图像的相邻像素水平相关性。表1列出了图像加密前后相关系数(水平,垂直方向)。由表1和图5可见,加密后图像相邻像素间的相关性要远小于Lena原图像的,这表明本算法具有较强的抗统计分析能力。
(3)差分攻击
攻击者通过图像中很小的一点(例如一个像素)来观察加密后图像的变化,来破解加密图像。这里作者以原始图像一个像素的改变对加密图像的影响为例测试了差分攻击。先定义了两个量:归一化平均变化强度(UACD和像素变化率(NPCR)。令加密图像(两幅)分别为C1和C2,这些图像只有一个像素的改变。像素在位置(i,j)的灰度值为C1(i,j)和C2(i,j)。定义一个二值矩阵D,它和C1与C2有相同的尺寸。若C1(i,j)=C2(i,j),则D(i,j)=1;否则D(i,j)=0。
NPCR定义为:
![]()
UICI定义为:
![]()
经过计算可以得到NPCR=0.423%,UACI= 26.34%,由此可见本加密算法不仅仅对密钥是敏感的,对要加密的图像文件也是非常敏感的,可见可以有效的抵抗差分攻击。
通过以上实验结果表明本加密算法对密钥具有敏感的依赖性、抗攻击能力强,加密速度更快等优势。
小知识之差分攻击
差分攻击是一种选择明文攻击,其基本思想是:通过分析特定明文差分对相对应密文差分影响来获得尽可能大的密钥。它可以用来攻击任何由迭代一个固定的轮函数的结构的密码以及很多分组密码(包括DES),它是由Biham和Shamir于1991年提出的选择明文攻击。











