为提高图像文件加密效果,可结合混沌理论、位平面分解理论以及灰度置乱理论,获得一种加密新方法,即先对置乱后的图像进行位平面分解,再针对不同位平面使用不同的混沌加密密钥进行加密。
一、混沌系统
1、混沌系统简介
混沌现象是自然界中比较常见的一种动力状态,其科学定义是:有确定规则生成的、对初始条件具有敏感依赖性的恢复性非周期运动。可以看出,混沌系统具有以下特性:
(1)确定性
(2)有界性
(3)非周期性
(4)对初始条件具有极端敏感性
正是由于上述4种性质,混沌系统具有保密通信的极佳性能。混沌由确定性系统产生和具有有界性,意味着混沌系统是可以控制的,也是可以观测的;具有非周期性,说明它具有宽的频带和类噪声特点,将信号隐藏在噪声中,很难提取。对于初值敏感性说明混沌信号具有长期不可预测性,所以说混沌系统是一个良好的加密系统。
2、Logistic混沌系统
logistic映射是由生物学家R. May于1976年提出来的,它是一个非常简单的一维非线性迭代方程,其定义描述为:
![]()
其中0<xn<1,分形参数1≤μ≤4。它虽然简单但是有着极其复杂的动力学行为,它的演化过程与M有密切的关系,当3. 569999…≤M≤4时,系统工作于混沌状态。Logistic映射序列大部分分布在0和1附近,关于0.5对称分布,序列均值为0.5。人们对logistic映射进行了改进,提出了均值为0的满log istic映射(μ=2)。
![]()
对应的概率分布密度函数为:
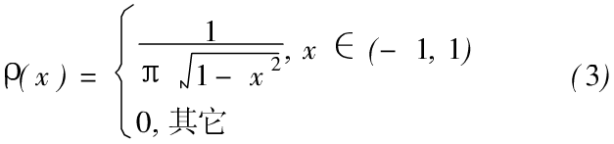
3、Chebyshev混沌系统
W阶chebyshev映射的定义为:
![]()
式中- 1< x<1,当ω≥2时,它是混沌和遍历的,而且具有正交性,这时不同的初始值无论多么接近,多次迭代出来的序列都互不相关。
4、位平面分解
对于一幅数字图像,总可以分解为多个位平面,不同的位平面代表了图像不同的信息,高位位平面代表了图像的轮廓信息,低位位平面代表了图像的细节信息,中间的位平面代表了图像的背景信息。对于不同位平面的处理相当于对图像不同信息位置的处理。例如对于一个副灰度值在0。255之间的灰度图像每一个像素点都可以表示为一个八位二进制数,所有点的相同位置上的数组合起来就形成了不同位平面。
5、Arnold置乱
Arnold变换是V.J.Amold在遍历理论研究中提出的一种变换,俗称猫脸变换,在Arnold变换种,对于一个N*N的数字图像,如果象素的坐标x,y∈( o,1,2,,,,,n-1),那么Arnold变换为:
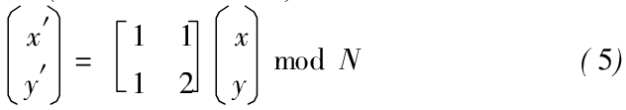
其中x,y为原图像中象素的坐标石x',y'为变换后图像象素点坐标。
可以看出经典的Arnold变换是针对图像行列一样的变换,对于经典的Arnold变换进行改进使之可以对于任意大小的图像都可以进行变换,改进后的Arnold变换为:

相当于:
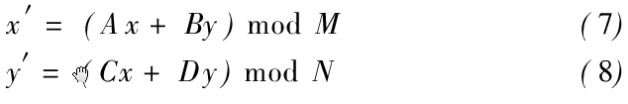
M为图像的行点数,N为图像列点数,A、B、C、D为变换矩阵。
二、基于图像位平面分解混沌加密方法
1、加密方法及步骤
通过将混沌加密理论应用于图像的位平面分解中,形成了一种有效的加密方法。
加密步骤如下:
(1)读取图像,对图像进行预处理。
(2)将图像进行位平面分解。
(3)混沌系统产生混沌加密密钥序列key。
(4)根据加密密钥判断采用哪种加密系统,提取加密密钥key中的8个值作为加密系统的初始值,从而产生8组加密序列。对不同的位平面用不同的加密序列加密。其中加密系统一采用上文提到的Chebyshev混沌系统,加密系统二采用改进后均值为零的logistic混沌系统。设明文为c,密文为m,加密序列为k,则加密方法表示为m=c xor k。
2、加密效果及分析
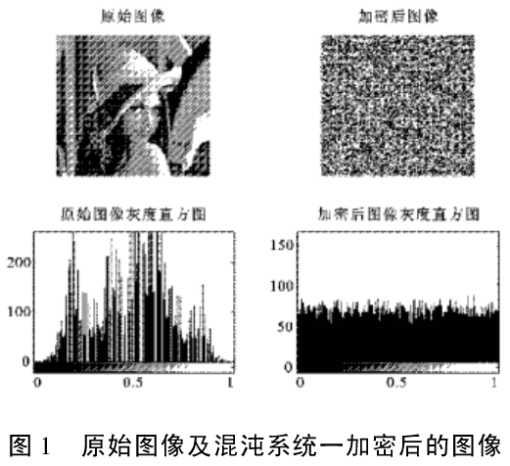
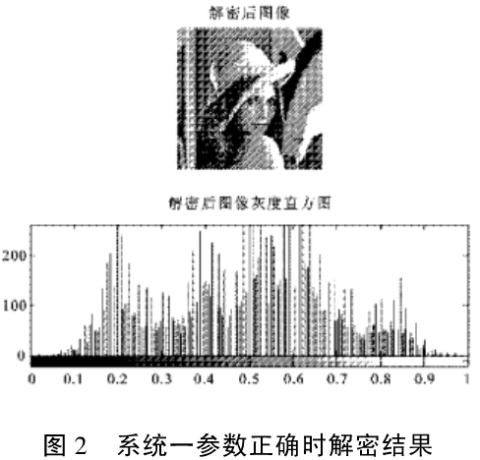
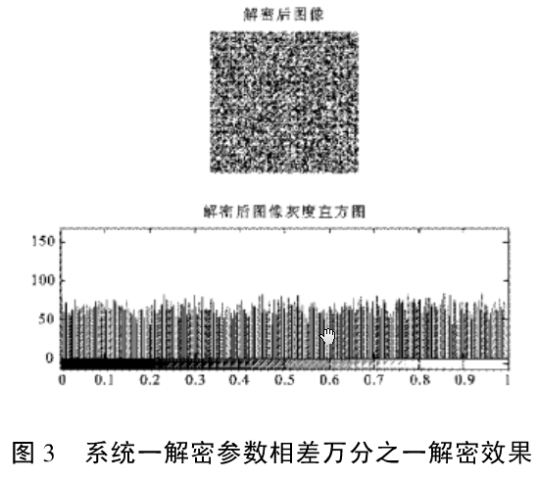
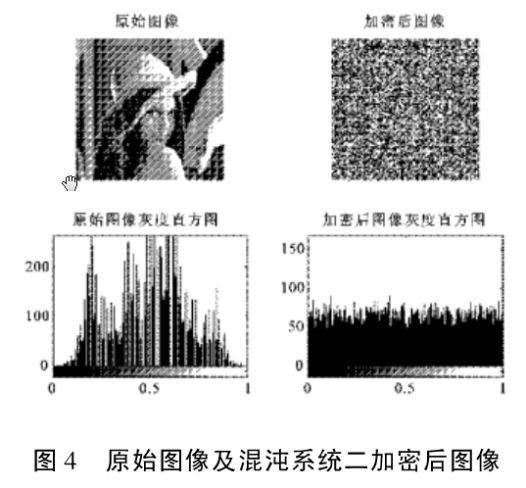
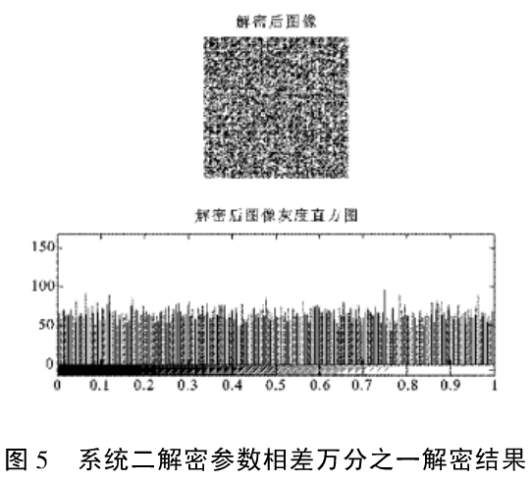
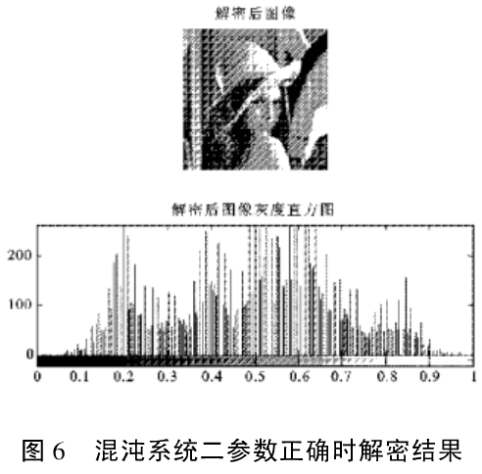
对于大小为131x 131的lina jpg图像根据文中提出的加密方法进行加密,效果如图1到图6所示,图1,图2,图3是用混沌系统一加密、正确参数解密,错误参数解密效果,可以看出加密后图像变得完全不可识别,只有解密参数正确时才能恢复原始图像,参数相差万分之一时解密后得到的图像是一个不可识别的图像。图4,图5,图6是用混沌系统二加密解密效果,可以看出与系统一有同样的效果,只有参数完全正确才能得到正确的图像。
3、结果分析
(1)直方图分析
通过观测加密后和加密前后图像的直方图,可以清楚的看到加密后直方图变得更加均匀,接近于噪声分布,说明加密后的图像给攻击者提供了比原始图像更少的信息,有利于信息的保密传输。
(2)信源熵分析
![]()
其中p (si)表示信号Si的概率日为信源熵。
一幅图像的信源熵能够显示出各个灰度值的分布情况。灰度值分布的越均匀,图像的信息量就越大,反之亦然。一般来说,一幅图像的灰度值分布不会很均匀,所以信源熵就很小。因此,如果加密后的图像信源熵变得越大,则图像的灰度值分布就越均匀,这就使得攻击者不能通过对信源熵的分析来获得图像信息。
通过计算,原始图像的信源熵是6. 9584,通过加密系统一加密后信源熵为7. 9910,系统二加密后信源熵为7. 89792,可以加密后信源熵接近于最大熵8,可以看出信息的遗漏是负值,所以从信源熵攻击的角度讲,此加密算法是安全的。
(3)密钥空间分析
密钥空间足够大才能抵御各种各样的强力量攻击。实验结果显示,本加密算法对密钥有很强的依赖性,只要解密密钥稍有变化,解密的图像就和原始图像有很大的差别,解密参数相差万分之一时都不能正确解密。此加密算法中使用了三个不同的混沌系统,每一个混沌系统都有一个初始密钥和控制参数,灰度置乱采用Arnold置乱方法,置乱矩阵可以变化,一共需要7个参数共同配合才能完成加密解密,密钥空间很大。
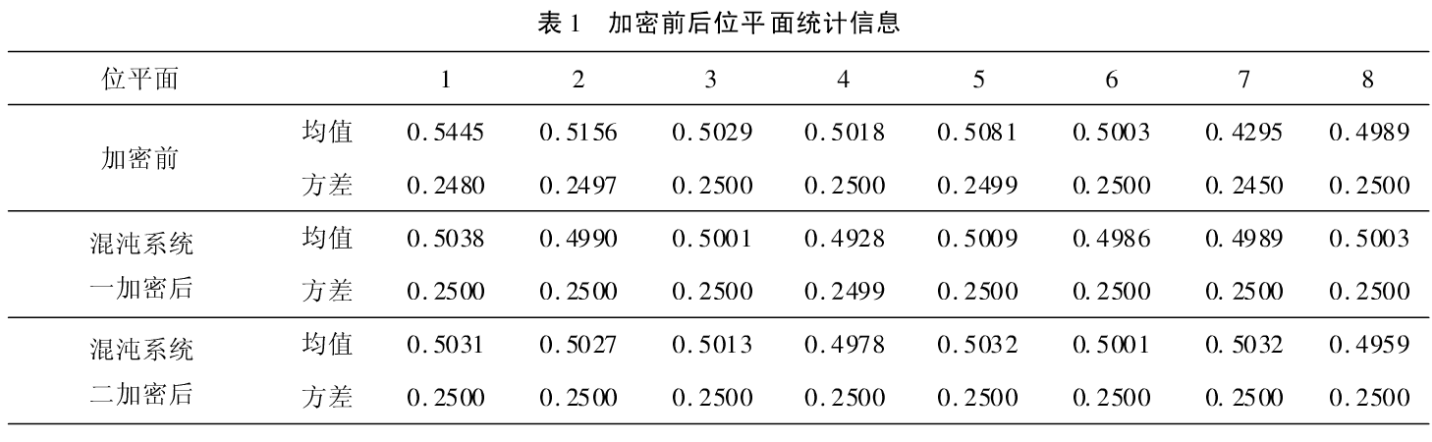
(4)位平面信息分析
经过仿真计算得出加密前后位平面统计信息如表1所示,可以看出经过加密处理后图像位平面信息有所变化,多数位平面均值变得更接近于0.5,说明0和1的概率分布更加均匀,对于通过位平面分解来获得图像信息的攻击有很好的抵抗作用。
小知识之信源熵
信源各个离散消息的自信息量的数学期望(即概率加权的统计平均值)信源熵的单位是 Bit/sign。











