鉴于一维分段线性映射的参数只有一个,很难保证加密算法的安全性,因此,我们提出了一种将一维分段线性映射推广至二维平面,得到平面上的二维分段线性映射,并且证明了二维分段线性映射具有混沌特性,作为一个应用,将其与图像相结合,利用二维分段线性映射生成的两个序列对图像文件加密,可以更加有效的解决一维分段线性映射由于生成序列过长而导致的周期退化问题,从而保证了加密算法具有一定的安全性。
一、二维分段线性映射及其性质
有资料给出了一种具有良好随机统计特性的一维分段线性映射的具体形式,定义如下:
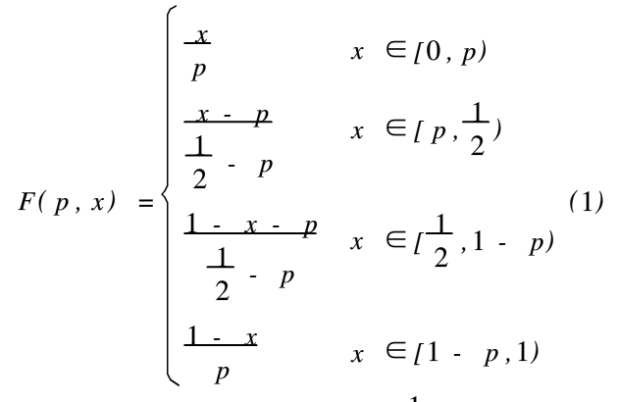
其中,控制参数p的范围为p∈(o,1/2),在初值x和控制参数p给定后,经过循环迭代得到[0,1]上的随机序列,式(1)生成的随机序列具有以下良好的统计特性:
(1)其Lyapunov指数大于零,系统是混沌的,输出信号满足遍历各态性、混和性和确定性;
(2)具有一致的不变分布密度函数,f(x)=1;
(3)输出轨道近似自相关函数_τ(n)=σ(n);
由于一维分段线性映射的生成序列具有良好的统计特性,文中将其进行推广得到平面上的二维分段线性映射,定义如下:
![]()
其中,F( p,x)的定义为公式(1),F(t,y)的定义为:

二维分段线性映射具有两个控制参数p,f,其范围分别为p∈(o,1/2),t∈(o,1/2)。下面证明二维分段线性系统Fx,y(p,f,x,y)=(F( p,x)F(t,y))是混沌的。
系统中是否存在混沌运动主要是通过判断系统最大的Lyapunov指数是否大于0决定的,因此只需要验证二维分段线性映射最大的Lyap unov指数与0的关系即可得知系统是否是混沌的。
二维分段映射可以改写为:
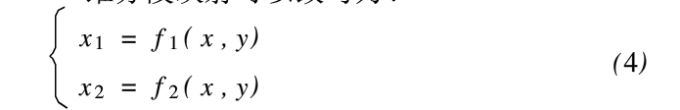
考虑到映射生成序列之间存在一定的关系,式(4)给出了点(x,y)与其后继点(x1,y1)之间的关系,其中f1与f2表示它们之间的抽象关系,若初始点x0和y0的偏差分别为σxo和σy0,从初始点( xo,yo)出发,由式(2)得到依次迭代的点为( x1,y1),( x2,y2),...,(xn,yn),前(n-1)个J accobi矩阵为:
![]()
且有:
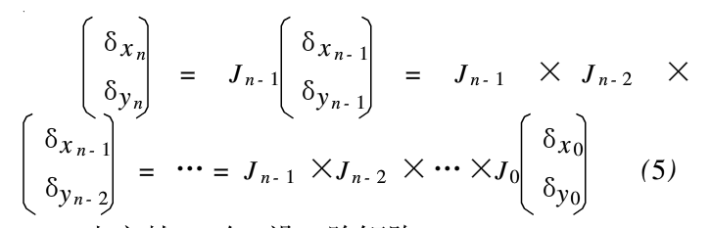
设二阶矩阵J=Jn-1×Jn-2×…XJ0,它的两个特征值分别记为A1和A2,则二维分段纷性映射的两个Lyapunov指数为:
![]()
为了判定系统最大的Lyapunov指数与0的关系,考虑到系统的Lyapunov指数与特征值之间存在的关系,转而考虑系统的Jaccobi矩阵的行列式与1的关系,当行列式大于1时,表明至少有一个特征值大于1,保证了至少真厂个Lyap unov指数大于o,从而可知系统是混沌的.
二维分段线性映射的Jacobin矩阵为:
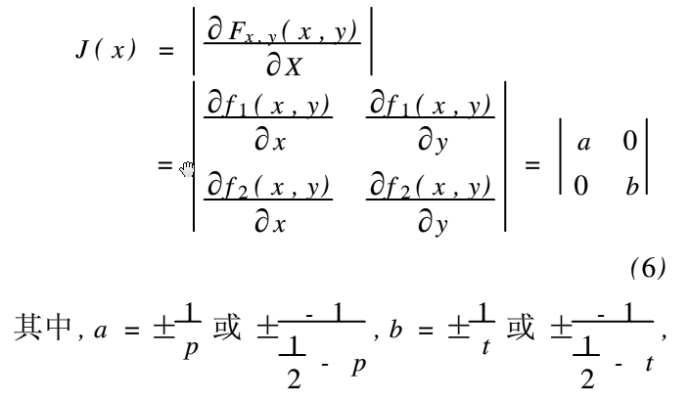
系统参数p,t∈(o,1/2)。则有|J(x)|=|ab|>1,因此二维分段线性映射是混沌的。
二、迭代序列比较分析
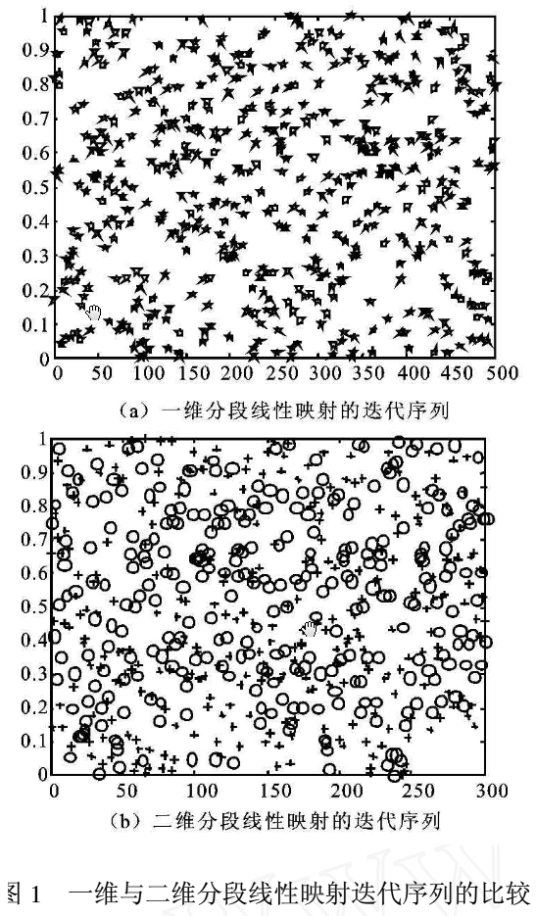
将一维分段线性映射推广至平面生成二维分段线性映射,以下通过实验仿真得到一维与二维分段线性映射生成的序列整观察可知,二者的生成序列具有类似的随机性,从图(1)的(a)中可以直观的看出,对于随机给定的初值与参数,一维分段线性映射的生成序列具有随机性,并且可以遍历整个值域,图(b)表示二维分段线性映射的两个生成序列,其中“+”表示一个序列,“0”表示另一个序列,可以直观的看出两个生成序列可以遍历整个值域,反映了二维分段线性映射的生成序列与一维分段线性映射的生成序列具有相似的随机性质。
三、二维分段线性映射在图像加密中的应用
传统的图像加密算法主要分为基于像素点位置的变化和基于像素点灰度值的变化两种,基于像素点位置的变化是指通过一定的排列算子对像素点的位置进行置乱,使图像看似变得杂乱无章,对于排列算子已知的算法,由于加密算法与密钥无关,所以容易受差分密码分析的攻击,并且变换前后图像的直方图并不改变,增大了被破译的可能性,为了更好的保护图像中的信息,通常是将两种方式结合使用,既改变图像像素点的位置又改变像素点的灰度值,使得攻击者无法利用差分密码分析攻击加密结果图像,文中利用二维分段线性映射得到两个序列,分别用于像素点的灰度值与位置变化,以达到更好的加密效果。
设原始图像AM×N为M行N列,对像素点灰度值的变化采用异或运算,从二维分段线性映射生成的两个序列中选取一个序列,依次取长为M×N的—段,进行扩大取整,由于灰度图像灰度值的范围为O~255,所以取整倍数定为255,将其转化为与图像大小相同的矩阵形式,称为随机矩阵,与图像相结合,对两个矩阵每一个对应位置处的像素灰度值与随机矩阵侑进行异或运算,得到灰度值改变后的结果图像。
对像素点位置的变换采用循环移位运算,从生成的另一个序列中依次取长为( M+N)的一段,进行扩大取整,扩大倍数可以随机选取,得到的整数序列称为随机序列,其中前M个随机整数分别与图像的M行相对应,用于行循环右移操作,循环右移的位数为与该行对应的随机整数,后N个随机整数分别与图像的N列相对应,用于列循环下移操作,循环下移的位数为与该列对应的随机整数,这样就可以实现图像的加密操作。
(1)加密步骤
Step1:随机生成所需的初始参数,利用二维分段线性映射得到两个随机序列,分别进行扩大取整,生成随机矩阵与随机序列。
Step2:将待加密的图像矩阵与随机矩阵相结合,将两个矩阵对应位置处像素点的灰度值分别进行异或运算,得到灰度值改变后的结果图像。
Step3:将灰度值改变后的结果图像与随机序列相结合,取随机序列的前M个随机整数用于M行的循环右移,后N个随机整数用于N列的循环下移,得到加密后的结果图像。
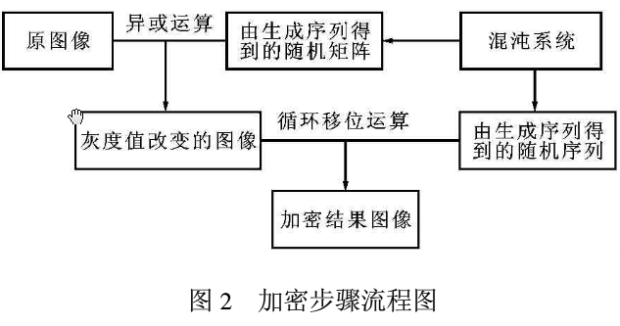
具体的加密流程如图2所示。
(2)解密步骤
Step1:接收方根据接收到的初值重构出用于加密图像的两个混沌序列,分别转化为随机矩阵与随机序列。
Step2:首先进行循环移位加密的解密,行的循环右移对应于行的循环左移,列的循环下移对应于列的循环上移,利用重构的随机序列得到循环移位解密后的结果图像。
Step3:进行异或运算加密的解密,由于异或运算具有的特殊性质,可以将经过循环移位解密后的图像与得到的随机矩阵进行异或运算,得到解密后的结果图像。
四、实验结果
对256 ×256的Lena图像文件加密、解密操作,图3给出了用文中加密算法对图像文件加密的结果图像及其对应的灰度直方图,以及当解密时初值有微小变化得到的错误解密结果图像。
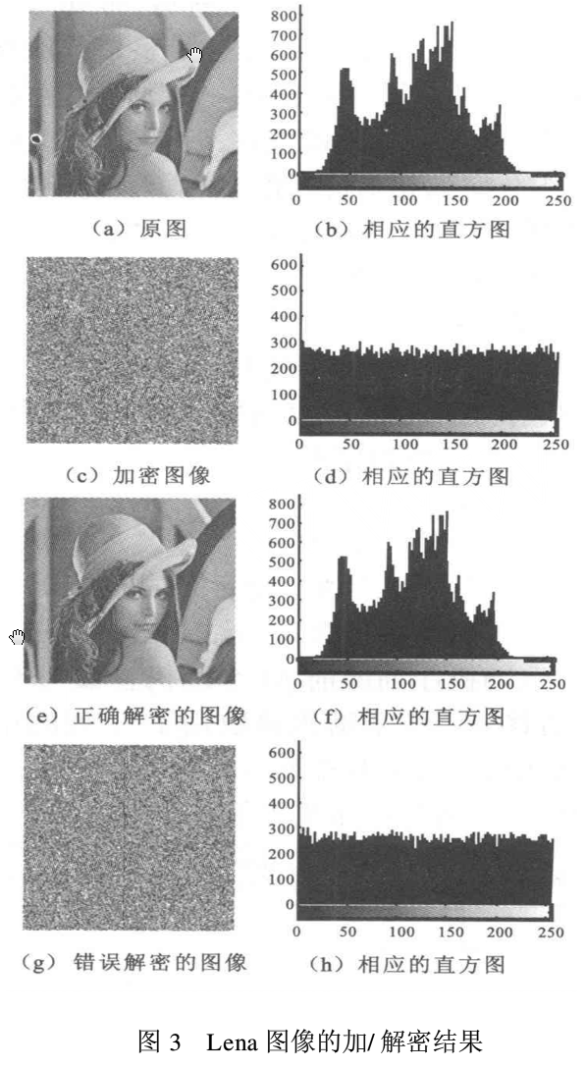
在本实验中,初值均为随机选取的,加密图像所用参数的值分别为:分段线性映射的初值为x=0. 6068,y=0.4860,控制参数,p=0.4751,t=0. 1156。当一个控制参数有0.000001的变化时便不能正确解密文件加密结果图像。
从图3的实验结果可知:首先,本加密算法对图像的直方图做了极大的改变,使得图像文件加密结果是图像的直方图较原图像的直方图而言看似更加平滑,降低了被攻击的可能性,其次,算法的密钥包括:混沌系统的初值,参数以及取整倍数,因此,加密算法具有足够大的密钥空间,并且算法对系统初值具有高度的敏感性,可以有效的抵御攻击者的统计分析攻击。
实验结果表明,利用二维分段线性映射给图像文件加密时可以得到较好的加密效果。
小知识之分段线性映射
分段线性映射指两个单纯形间的映射,它限制一个点(不是顶点)附近是线性的。









