基于小波变换的数字图像加密算法

小波变换是傅里叶变换发展史上里程碑式的进展，小波变换在时域和频域上同时具有良好的局部化性质，并对各种信号特征进行多分辨率分析有极大的适应性，已广泛用于信号与图像处理、语言识别与合成等科技领域。那么今天我将给大家介绍一种基于小波变换的数字图像加密算法。

一、二维离散小波变换

为表示一维信号而发展起来的一维离散小波变换可以很容易地推广到二维的情况。与图像变换一样，我们考虑二维尺度函数是可分离的情况，也就是：

式中：φ(x)是一个一维尺度函数，若Ψ(x)是相应的小波，那么下列3个二维基本小波Ψ1(x，y)=φ(x)Ψ(y)，Ψ2(x，y)=Ψ(x)φ(y)，Ψ3(x，y)=Ψ(x)Ψ(y)。

就建立了二维小波变换的基础.注意这里使用的上标只是索引而不是指数。具体说来，函数集{Ψlj，m，n(x，y)}={2jΨl(x-2jm，y-2jn)}，j≥0_l=1，2，3。

式中：j，l，m，n为整数，是L2(R2)下的正交归一基。

1、正变换

从一幅N×N的图像f1(x，y)开始，其中上标指示尺度并且N是2的幂。对于j=0，尺度为2j=20=1，也就是原图像的尺度。j值的每一次增大都使尺度加倍，而是分辨率减半。

在这里用j表示分辨率的索引，而不是尺度。

在这种情况中j≤0，而且在下面的等式中符号也要反过来。

图像可以依据二维小波按如下方式扩展。在变换的每一层次，图像都被分解为4个四分之一大小的图像，如图1所示，这4个图像中的每一个都是由原图与一个小波图像的内积后，在经过x和y方向都进行2倍的间隔抽样而生成的。

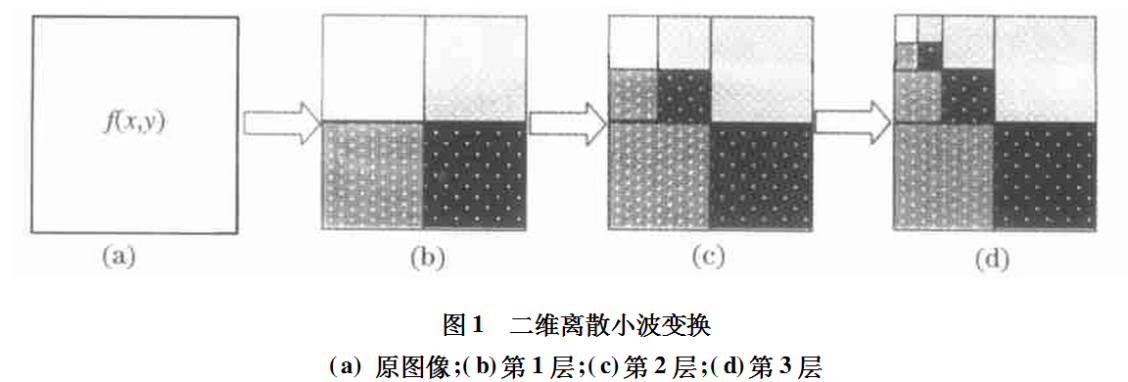
对于第1个层次(j=1)，可以写成：

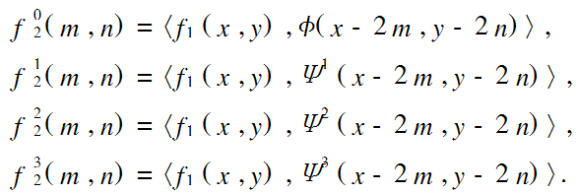
而对于后续的层次(j>0)，f02j(x，y)，都以完全相同的方式分解而构成4个在尺度2j+1上的更小的图像[图1(c)]。最终的结果是一个类似于Haar变换的配置，如图1(d)所示。将内积写成卷积形式，可有：

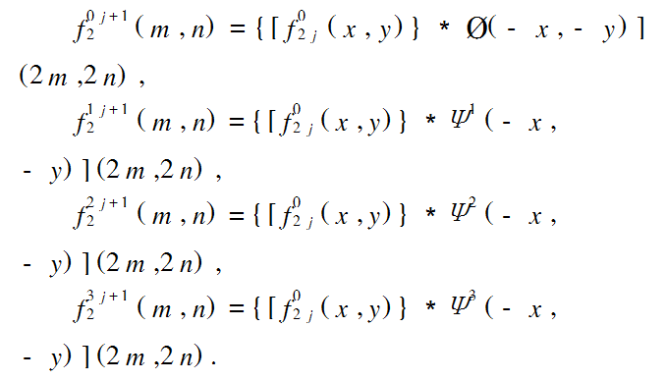
并且在每一层次进行4个相同的间隔抽样滤波操作。因为尺度函数和小波函数都是可分离的，所以每个卷积都可分解成在f02j(x，y)的行和列上的一维卷积。图2显示了这一过程。

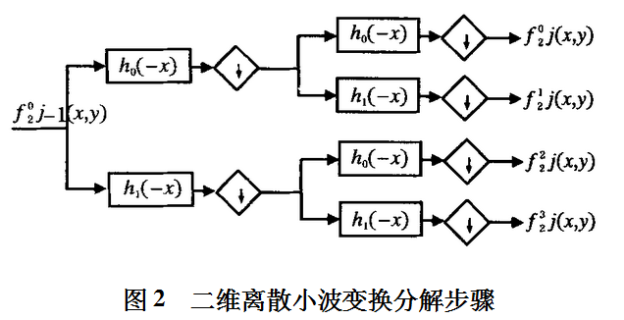
这样一来，二维可分离小波变换可以快速计算.变换过程能执行到层，对于N×N像素的图像，整数J≤log2N。如果变换系数能计算到浮点精度，那么用逆变换重建的图像就只有微小的失真。

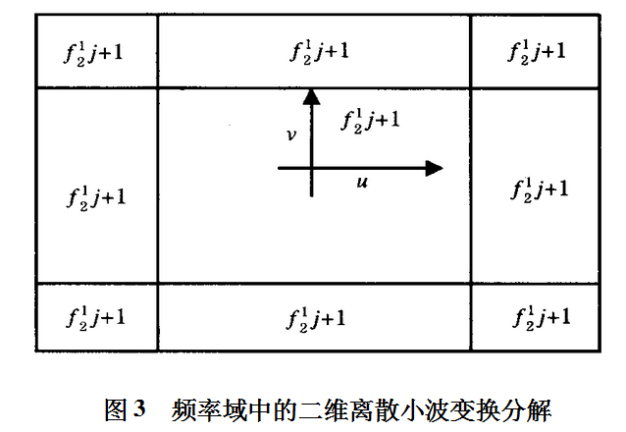
图3显示了下一尺度4幅图像中的每一幅在频域平面中的位置，如果使用的是sinc小波(也就是理想的半带低通和高通滤波器)。在每一尺度下，f02j(x，y)包含前一阶段的低频信息，而f12j(x，y)，f22j(x，y)和f32j(x，y)，和分别包含横向、纵向和对角方向的边缘信息。

2、逆变换

逆变换是通过与刚才所述类似的过程来实现的。这一过程可图解为图4。在每一层(例如最后一层)，都通过在每一列的左边插入一列零来增频采样前一层的4个阵列；接着像图中那样，用h0(x)或h1(x)来卷积各行，再成对地把这几个NΠ2×N的阵列加起来;然后通过在每行的上面插入一行零，将刚才所得两个阵列的大小增频采样为N×N；再用h0(x)和h1(x)与这两个阵列的每列卷积，如图4所示。而这两个阵列的和就是这一层次重建的结果。

二、基于小波变换的数字图像加密

1、数字图像水印信息

在这里将文件加密作为数字水印信息。图5和图6(a)分别显示了DWT图像分解和原始图像，从中可以看到，其对角方向矩阵主要是对角信息的变化情况，它的值一般为小数，并且数值很小，对显示的图像影响较小，因此比较有利于信息的隐藏。

图6(b)显示了将数字水印信息加入对角方向信息后DWT图像重建图，从中可以看到，在将信息经过灰度处理后，DWT重建图像与原始图像图基本没有差别，基本无法分辨图像是否失真。

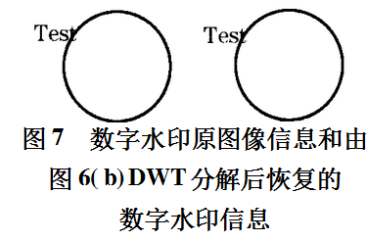
图7显示了数字水印原图像信息和由图6(b)DWT分解后恢复的数字水印信息，从中可以看到数字水印的信息被很好的恢复回来。

2、声音信息

在这里采用了MATLAB提供的声音文件，其中声音数据以小数[-1，+1]的形式出现，通过下式处理原始声音信息。

x(m)=[y(m)+1]×127

式中：x(m)为处理后的声音信息，y(m)为原始声音信息。

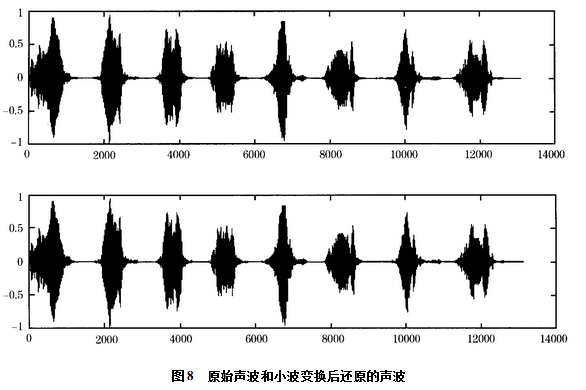
通过实验可以听到声音没有产生失真，通过图8的声音波形可以看到失真现象非常小，并且效果比较理想。

admin普通用户

海报分享