基于变参数的复合混沌系统,我们结合一维Logistic映射和三维混沌系统( Chen System),提出了一种基于变参数混沌的图像加密算法,通过构造一种非线性耦合函数来对明文像素点同时进行置乱和像素灰度变换,并根据由明文信息产生的密钥来对每轮置乱后的像素点采用不同方式进行图像文件加密。
一、_基于复合混沌系统变参数图像加密算法原理
1、 Logistic混沌映射
Logistic混沌映射是一种非线性混沌系统,其定义如下:
![]()
式中:μ为系统参数;w0∈(0,1).当3.569 94....≤μ≤4时,系统处于混沌状态。
2、三维混沌系统
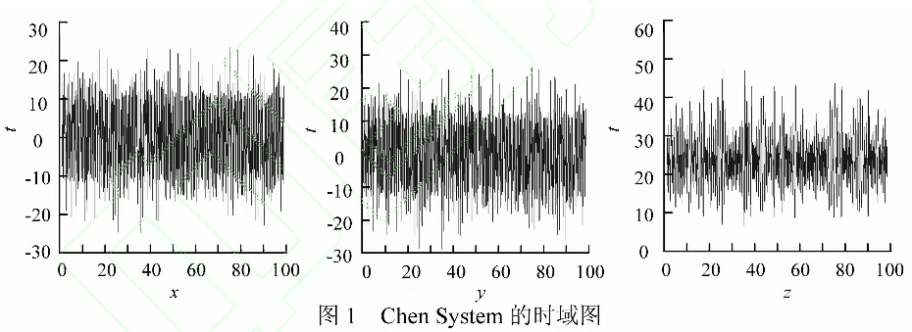
当a=35,b=3,C∈ [20,28.4]时,式(2)存在混沌吸引子,系统可以处于混沌状态,本文取系统初值x0,yo,zo为密钥,积分步长t=0.001,生成序列{ Xk,yk,zk}。其时域图如图1所示。
二、基于复合混沌系统变参数图像加密算法思想
首先利用Logistic映射迭代选出其加密所需的系统参数值,然后结合三维混沌系统构造一种非线性耦合函数并对明文同时进行像素置乱和灰度变换,设明文图像的大小为M×N。
1、_基于复合混沌系统变参数图像加密算法设计
首先,给定两个参数μ1,μ2,迭代式(1)([(wo ×(M+N))+100])次,定义参数选择函数,即:
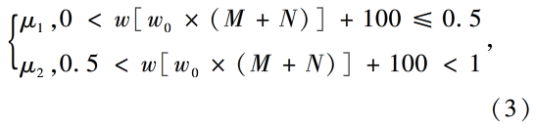
可得到其中之一为所选参数,令其为置乱步骤中所用式(1)的参数,则另一个为灰度变换步骤中所用式(1)的参数。设图像的像素点坐标为(i,j),对应的像素值为I(i,j),设计图像特征密钥![]() ,并构造耦合函数如下:
,并构造耦合函数如下:
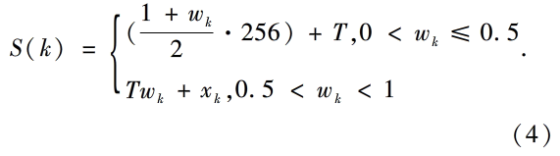
由函数S(k)可设计置乱变换为:
![]()
其中,加密时以先行后列的顺序遍历图像的每个像素点,在上述置乱系统中,(i,j)为原像素点位置坐标,(i',j’)为置乱后的该点的位置坐标。
对每一次置乱后的明文像素点,采取下述的方式进行灰度值变换处理,即:
![]()
这里C(i,j)和C(i ',j')为像素点置乱后的灰度替代值。
2、基于复合混沌系统变参数图像加密算法步骤
步骤1 根据Logistic混沌映射选取置乱和灰度变换过程中的系统参数。
步骤2 遍历明文,设计加密算法所需密钥T。
步骤3 根据Logistic混沌映射和三维混沌产生的多维混沌序列构造一个非线性耦合函数。
步骤4根据设计的耦合函数以及式(5)对明文像素点进行置乱。
步骤5 对每一次置乱后的像素点根据(6)式进行灰度值替代。
步骤6 重复步骤4和5直至遍历整个明文图像。
步骤7 完成一轮加密操作,并根据实际需要进行多轮加密。
解密算法即为加密的逆过程,计算密钥并构造出耦合函数S(k),并根据式(5)和(6)对密文反解即可进行正确解密,得到明文图像。
三、仿真实验及安全性分析
一个安全的算法可以有效抵御各种攻击,如穷举攻击、统计攻击等,本文以MATLAB 7.1为平台,对该加密算法进行仿真实验,其中,以大小为256像素×256像素的Lena标准灰度图像作为明文图像,设初始密钥wo =0. 498 76,xo=13. 188,yo=11. 223,zo =0.1。
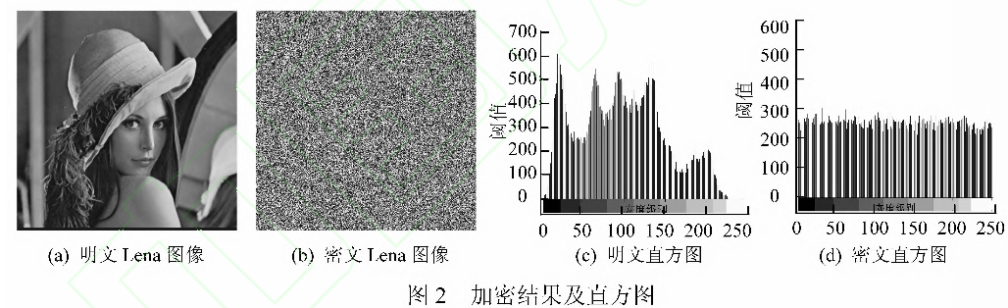
图2(a)为Lena原图像,图2(b)为加密后的Lena图像,图2(c)和图2(d)分别为明文和密文所对应的直方图,仿真实验表明,加密前后的图像与直方图有着很大差别,密文已经隐藏了原图像的人物轮廓,没有透露出明文图像的任何信息,这表明本文所采用的混沌序列具有良好的伪随机性和复杂性,从而保证了密文直方图分布均匀,可抵抗相应的统计攻击。
1、 密钥空间分析
一个好的加密方案应该具有足够大的密钥空间,从而使得穷举攻击变得不可行,本文算法密钥由wo,xo,yo,zo构成,设每个混沌系统的初值均有16位有效数字,则密钥空间为1016 ×4= 1064。此外,明文信息密钥丁亦作为密钥保管,因此,算法具有足够大的密钥空间,使得穷举攻击变得不可能。
2、 密钥敏感性分析
为了测试该算法的密钥敏感性,现将其中的一个密钥进行微小的改动( 10 -16),如令wo=0. 498 700 000 000 001,其余密钥保持不变,并对密文进行解密,加密解密图如图3所示。

由实验可知,当对密钥初值进行微小扰动后,便无法正确解密出明文图像,而解密出的图像也与原始明文有着很大差别,这说明该算法具有较高的密钥敏感性。因此,该算法可以有效地抵御敏感性攻击,并具有很好的安全性和实用性。
3、 像素相关性分析
一幅图像由于需要显示出一定的信息,因此,其像素之间有很大的关联,而一个好的算法便会降低这些相关性,从而达到可以抵御统计攻击,为了测试明文图像经本文算法加密后的像素点的水平、垂直以及对角方向的相关性,从明文图像和密文图像中随机选取1 000对像素对,并根据式(7)进行计算像素相关性系数,即:
![]()
式中:![]() ;x,y分别表示相邻2个像素的灰度值,计算结果如表1所示。
;x,y分别表示相邻2个像素的灰度值,计算结果如表1所示。
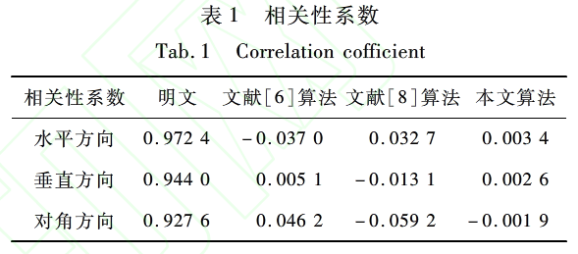
图4显示了明文与密文水平方向相关性,通过对比图4(a)和图4(b),明显可见,密文中相邻像素间的相关性呈随机对应关系,对比表1可知,加密后的图像的相关系数都趋近于0,相关性远小于原始明文图像,明文信息已很好地扩散到密文之中,这说明本文复合混沌系统所产生的伪随机序列具有较好的伪随机性。因此,该算法具有较强的抗统计分析能力。

4、差分攻击分析
密码攻击者经常利用差分攻击寻找明文和密文之间的关系,通过改变明文的一个像素点来观察密文的变化,进而进行破解密文,设位置为(i,j)的像素点的灰度值为C1(i,j)和C2(i,j)。定义一个二值矩阵D,见式(8)。
![]()
它和C1与C2,有相同的大小,若C1(i,j)=C2(i,j),则D(i,j)=0;否则D(i,j)=1.为了测试本文算法是否可以有效地抵御差分攻击,分别根据式(9)和式(10)测试NPCR(像素变化率)和UACI(归一化平均变化强度)2个值,差分攻击分析结果如表2所示。
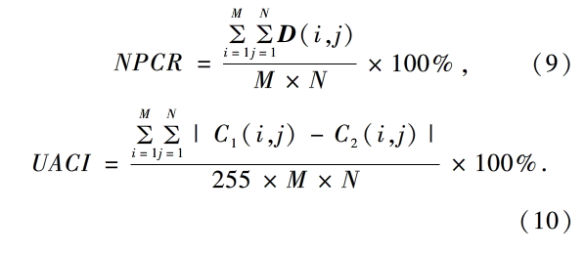

通过对本文算法差分攻击结果可知,本文加密算法仅需一轮加密即可达到理想值(NPCR >0. 996,UACI>0.334)。这说明,本文算法对明文信息更敏感,算法安全性与明文相关程度
更高,因而可以有效地抵御差分攻击,具有更高的安全性和实际应用价值。
5、 算法时间复杂度分析
为了测试所提算法的算法时间复杂度,本文以Matlab 7.1为实验平台,对加密算法进行仿真实验测试,实验结果如表3所示。
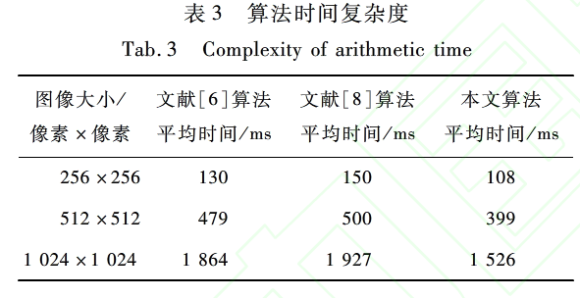
由表3可知,本文加密算法的加密时间更短,加密速度更快,效率更高;因此,本文加密算法具有更广的应用前景以及更高的实际应用价值。
小知识之线性耦合
线性耦合是数据耦合的一种。数据耦合是一个模块访问另一个模块时,彼此之间是通过简单数据参数 (不是控制参数、公共数据结构或外部变量) 来交换输入、输出信息的。而线性耦合输入、输出信息的变量是成正比的非线性耦合输入、输出信息的变量不成正比。











