目前广泛应用于加密的混沌模型主要有Logistic映射,其有着形式简单、产生混沌时间序列短等优点。如果在混沌加密之前,对图像数据进行小波变换,变换后得到的小波系数中如果有一个发生改变,就会通过小波变换的逆运算体现在所有的象素点中,这样的加密效果会更好。为此,我们引入两种混沌映射,设计了出了一种对二维小波分解所得到全部频率系数进行Zigzag置乱和应用混沌序列改变象素值相结合的图像加密算法。
一、Zigzag变换
Zigzag置换是一种置乱方法,通过对一个矩阵中的元素从左上角开始按“之”字形依次扫描取数来达到对数据进行置换。首先将扫描到的元素先依次存放到一个一维数组中,然后再将此一维数组按一定的方式置换为二维矩阵,则上述的置换过程可看作是对矩阵中元素的置换,这样的过程就叫做Zigzag置换。Zigzag置换的特点是算法实现简单,时间复杂度低。其在数字图像处理中应用比较多,基于Zigzag置乱在视频加密方法及图像数据压缩等方面已有广泛的应用。
在算法分析领域有两个很重要的概念:时间复杂度和空间复杂度,二者往往是矛盾的。在信息安全领域,往往更追求的是算法的时间复杂度低而相对不在意空间复杂度。如在AES加密过程中,其S变换使用查表的方法得到的程序,加密效率远远高于其他加密算法。在本文所设计的变换过程中也使用查表的方法完成Zigzag排列。下图给出一组8_8的Zigzag排列的系数的行列变换表及其逆变换表。
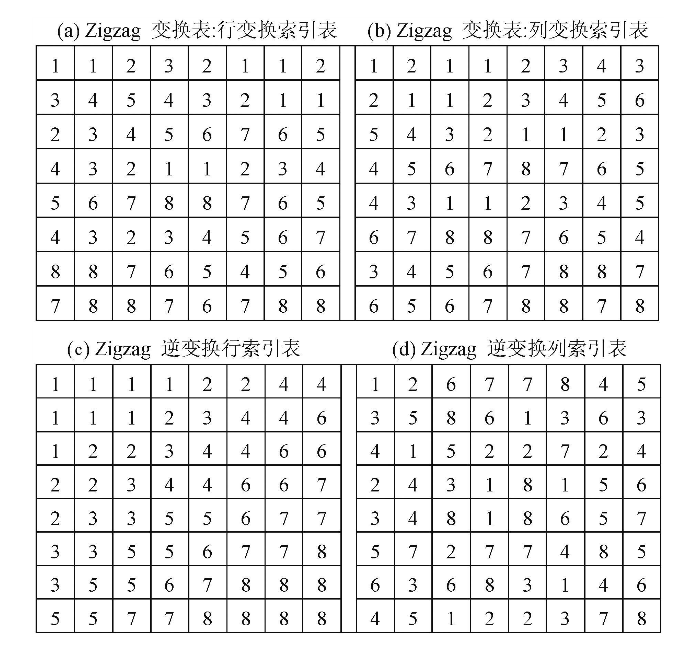
按照变换表就可以对一个8_8的矩阵I进行Zigzag置乱,具体置乱过程可由下式表示:
![]()
其中:z(i,j)表示置乱后矩阵i,j处的元素,r(i,j),c(i,j)分别为行、列变换索引表i,j处的元素。由相应的逆变换表可以得到原始矩阵。
二、混沌序列模型
混沌现象是在非线性动力系统中出现的确定性的、类似随机的过程,这种过程既非周期又不收敛,并且对初始值极其敏感,正是由于此性质,在信息安全中得到了广泛的应用。
1、Henon映射
Henon映射定义为:
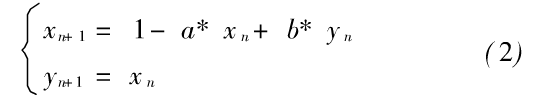
其中:a,b均为任意常数,b=1时为保面积映射,b<1时为耗散映射。参数取值为a=1.4,b=0.3,此时系统处于混沌状态。
2、正弦平方映射
正弦平方映射方程为:
![]()
上式中x0#R,且0<x0<1,当b>1时,其Lyapunov指数大于零,且Lyapunov指数λ=ln(b),系统工作在混沌状态。
3、初值敏感性测试
本文在这里设计了一种测试混沌序列初值敏感性的方法,以正弦平方映射为例来说明实现方法。设有两个初值,仅相差10-5,由这两个初值分别得到两组序列值,再计算出他们对应值的差值,进而可以绘制出初值敏感性图,部分代码如下。下图(a)、(b)画出了henon映射100步内的误差图,由图可知差异有时可达最大值,下图(c)给出了正弦平方映射50步内的误差图,差异有时甚至接近1。
x(1,:)=[0.4,0.400001];
fori=2:50
x(i,:)=sin(a*asin(sqrt(x(i-1,:)))).^2;
endy=x(:,1)-x(:,2);
figure,plot(y)

三、基于Zigzag变换及混沌序列的图像加解密算法
1、加解密过程
(1)基于Zigzag变换的置乱
考虑一幅大小为M_N具有N级灰度的图像,对其采用适当的小波基进行二维小波分解得到其全部频率系数,可以采用自己设计的一个随机置乱表代替Zigzag变换表和式(1),把所得到的频率系数转换成矩阵,然后对其进行8_8分块使用Zigzag变换表进行扫描。经扫描后得到一组置乱了的频率系数,再利用其进行二维小波重构,这样便得到了置乱后的图像。为了能使置乱效果更好,可以多次对频率系数进行变换。要想得到正确的图像,必须要用变换时使用的变换表得到其相应逆变换表和变换的次数n。因此,可以把所设计的变换表和变换次数n作为密钥,从而实现图像加密。
(2)混沌密钥模板序列生成及象素值变换
本文所设计的加密算法就是利用Henen映射、正弦平方映射对初值敏感的性质生成混沌序列作为密钥模板进而与象素值进行运算来得到一幅杂乱无章的图像。由于图像的灰度级为N级,其值从0~N-1,Henen映射、正弦平方映射产生的混沌序列值不在此范围之内。为了将以上映射产生的混沌序列与图像象素值运算,需做一些适当的修正,把所生成的值映射到集合{0,1,2_,N,N-1}。
a、混沌密钥模板序列值的修正
设Henen映射,正弦平方映射所生成的混沌序列分别为r1,r2,r3。为了方便后边的运算,使用Matlab中的reshape函数将r1,r2,r3转换成矩阵的形式,称为密钥模板矩阵。可用式(4)进行修正。
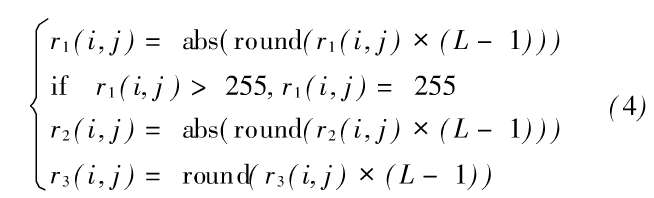
其中,round()函数为取整,abs()表示求绝对值。
b、象素值变换
设I(i,j)为图像(i,j)坐标处的象素值,其中1_i_M,1_j_N,I(i,j)为(i,j)坐标处变换后图像的象素值,本文采用r1,r2,r3设计象素值变换映射,可由式(4)表示:
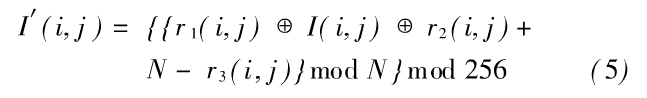
N是图像的颜色深度(对于256级的灰度图像,N=256),⊕代表按位异或运算,mod代表求模运算。为了增加密文图像的安全性,可以多次进行上述过程。这部分所用密钥为:key1=(x01,y01,x02,b,n),x01,y01为式(2)的初值,x02,b为式(3)的初值和参数,n为迭代次数。为了提高图像加密过程的效率,对于待加密的原图像可以进行分块处理。解密是加密的逆,其逆运算式为:
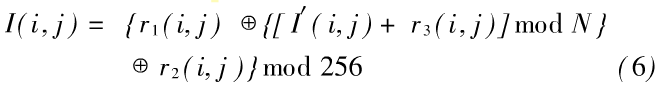
由此式就可完成象素变换的解密运算。
c、加密算法
对明文图像I进行小波分解得到分解的全部频率系数,对其进行Zigzag变换,然后用此结果进行二维小波重构得到一次加密结果I1。
应用混沌序列模板r1,r2,r3及式(5)对I1进行加密得到密文象素流I1(i,j),可重复步骤(1)、(2)两步多次。解密算法是加密过程的逆。
3、算法思想的扩展
在上节中主要描述了对一幅灰度图像的加密过程,本算法也可应用于彩色图像,具体过程是分别提取彩色图像的R,G,B颜色分量,分别对其进行3.1节所述的加密,然后对3个加密结果使用cat函数就可得到加密后的结果。同时在加密算法中,需要3个密钥模板,则还可以使用三个不同的混沌映射来得到,在加密彩色图像时,对每个分量加密时可以选取不同的初值和参数,这样可以大大增大密钥空间。
四、仿真试验及结果分析
在Matlab7.0编程环境下,本文首先按照上面所述的加密算法对大小为96_96的lenna灰度图像进行了加解密试验,然后又按上面所述思想实现了彩色图像的加解密。在试验中,对图像使用haar小波基进行二维小波分解,key1中的参数x01=0.2,y01=0.1,x02=0.5,b=3.9,n=1,试验结果如图所示:
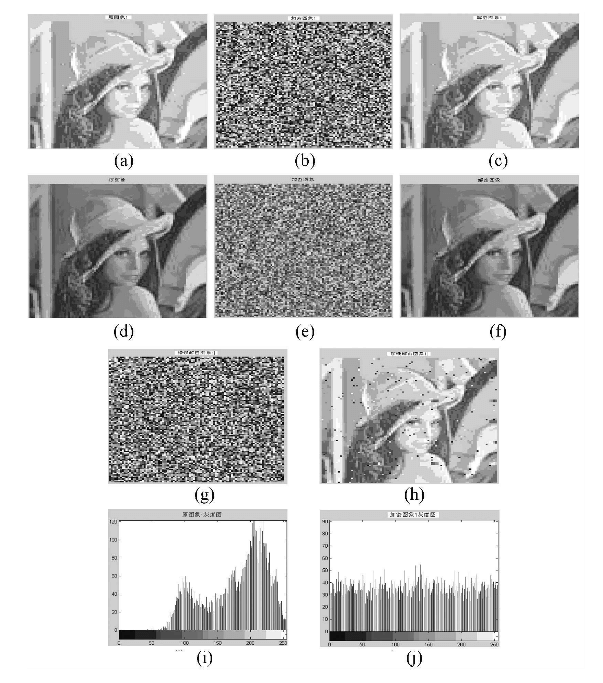
由上图(b)、(e)可看出加密后的图像已是一幅无纹理,杂乱无章的图像,从中不能得出原图像的任何信息,得到了理想的加密结果。
1、算法的安全性分析
在信息安全领域,Kerckhoffs准则认为:一个安全保护系统的安全性不是建立在他的算法对于对手是保密的,而是应该建立在他所选择的密钥对于对手来说是保密的。
2、密钥空间分析
由上文加密算法的描述过程可知,该加密系统使用了Zigzag变换表和两个不同的混沌系统。Zigzag变换表由两个8_8行、列索引表构成,其可以作为密钥,在混沌序列的产生过程中,需要3个不同的初始条件和1个参数以及加密次数,由此可见密钥空间是非常大的,可以有效地抵抗穷举攻击。
(1)密钥敏感性测试
上图(g)是当解密时只把x02的值做了微小的变化得到的解密结果,其中x02=0.500000001。结果表明,解密结果是一幅杂乱无章的图像,解密失败。体现了很好的密钥敏感性,同时也达到了密码学中混淆和扩散的目的。
(2)抗恶意攻击
当第三者截取到杂乱无章加密图像但无法获取解密密钥就不可能得到明文图像,则其就可能对密文图像进行加噪、剪切等恶意攻击来破坏图像。上图(h)是加密图像受加椒盐噪声攻击的解密结果,可看出解密结果虽然有一些噪声颗粒,但整个图像轮廓还是可见的。实验过程也做了其他攻击,结果都体现了算法的鲁棒性。图像中相邻象素间存在较大的相关性,利用这一固有性质可以进行统计分析攻击。上图(i)是原图像的灰度值统计直方图,上图(j)是文件加密图像的象素直方图。
可见,加密过程将原始图像灰度值的不均匀分布变成了灰度值的均匀分布,使密文灰度值在[0,255]整个空间范围内取值概率均等,使明密文的相关性大大降低,体现了算法抗统计分析攻击的能力。
对于彩色图像可得到相同结果。
本文给出了基于小波分解所得到的频率系数的Zigzag置乱和应用两个混沌系统生成相应的混沌序列经修正后转换成图像加密模板矩阵,进而应用这两个加密模板对象素值进行变换的加密算法,该算法易实现。
小知识之Kerckhoffs准则
密码学上的Kerckhoffs准则(也称为柯克霍夫假说、公理、或定律)系由奥古斯特·柯克霍夫(Auguste Kerckhoffs在19世纪提出:即使密码系统的任何细节已为人悉知,只要密匙(key,又称金钥或密钥)未泄漏,它也应是安全的。_信息论的发明者克劳德·艾尔伍德·香农(Claude Shannon)则改成说:“敌人了解系统”,这样的说法则称为香农箴言。 它和传统上使用隐密的设计、实作、或其他等等来提供加密的隐晦式安全(Security through obscurity)想法相对。











