目前常用的图像置乱方法有Arnold变换、幻方变换、Tangram算法、Conway游戏、Gray码变换等。Arnold变换算法简单且具有周期性,所以在图像信息隐藏方面得到了很好的应用。下面我就给大家介绍一种基于改进的Arnold变换和扩展的多维Arnold变换并且加入了Logistic混沌映射的图像加密算法。
一、关于Arnold变换
设有单位正方形上的点(x,y),将点(x,y)变到另一点(x′,y′)的变换为:
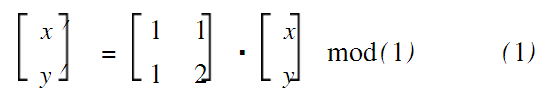
此变换称作二维Arnold变换,简称Arnold变换。可见Arnold变换实际上是一种点的位置移动。
对于正方形数字图像,我们可以把其表示成:
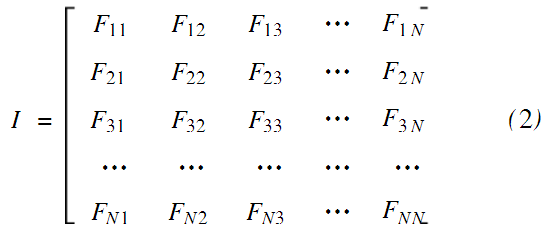
式中N是数字图像矩阵的阶数;Fxy表示坐标为(x,y)的像素点的灰度值。将Arnold变换应用在数字图像上,可以通过像素点坐标的改变而改变图像灰度值的布局,把数字图像看作一个矩阵,可由式(3)实现图像像素点的置乱。

式中(x,y)是原图像中像素点的位置坐标;(x′,y′)是变换后该像素点对应的位置坐标。
对于二维平面上的位置变换来说,可以由上述的Arnold变换推广出一类变换,满足“位置移动”的要求。有专家证明了对于如下2×2的变换矩阵:![]() ,当其元素满足ad-bc=1时,它对平面坐标的变换可作为一种置乱变换,所以可将Arnold变换推广为:
,当其元素满足ad-bc=1时,它对平面坐标的变换可作为一种置乱变换,所以可将Arnold变换推广为:
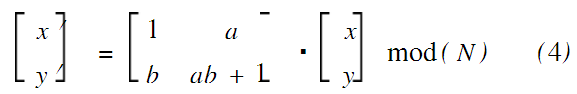
式中参数a,b是正整数;N是数字图像矩阵的阶数。
另外还有专家将Arnold变换推广到高维的情形,相应的变换矩阵为:
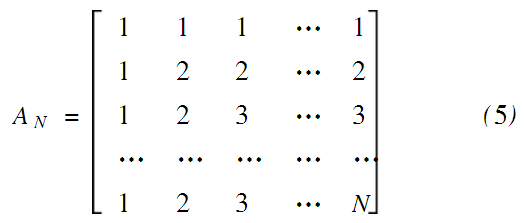
对于矢量(x0,x1,…,xN-1)T,做如下变换(x′0,x′1,…,x′N-1)T=AN(x0,x1,…,xN-1)T,这就给定了一种在N维空间上离散网格点的移动方式。
二、图像加密、解密算法
1、图像加密算法
(1)位置置乱
首先产生Arnold变换的参数a,b值的序列,利用简单的logistic混沌映射来实现。
Logistic映射的函数式如:
![]()
其中当μ=4时系统处于混沌状态,此时系统产生的序列具有随机性,遍历性,对初值的敏感性,其范围为(0,1)。以K1和K2为初值产生两个混沌序列,其中K1和K2的范围亦为(0,1)。对产生的两个混沌实值序列均从第一百个实值开始取用,组成实值序列X1和X2。
对于实值XK(i)=0b1b2b3b4b5…序列YK由式(7)得到:
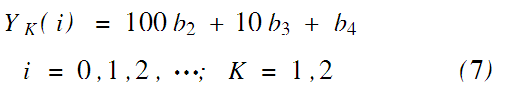
然后把Y1(i)和Y2(i)的值分别赋给参数ai和bi。
![]()
设方形图像Fxy的大小为N×N,即x∈[1,N],y∈[1,N],利用式(9)对整个图像做变换,变换迭代n1次所得图像记为F′xy:
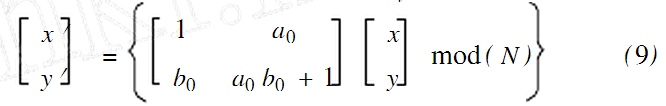
式中x和y分别表示原图像矩阵像素点的横纵坐标;x′和y′分别表示图像经Arnold变换后图像矩阵的像素点横纵坐标。
将图像F′xy分为B×B块,每块有N2/B2个点。将最终加密的密图F″xy分成N2/B2块,每块有B×B个点,使N2/B2μB2。图像F′xy和位置置乱后图像F″xy的分块矩阵分别记为Block1和Block2,Block1可表示为:
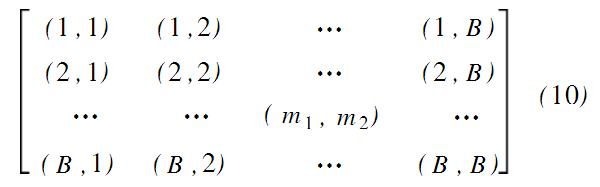
其中(m1,m2)为图像F′xy分块矩阵的块位置坐标,取出F′xy的每个分块,对其进行n2次Arnold变换,每块做变换所取的a,b值都是不同的,如式(11)所示。
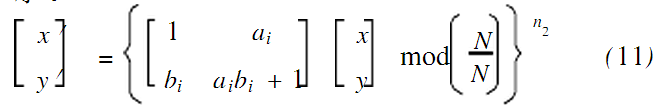
式中x=1,2,…,N;y=1,2,…,N;x′=1,2,…,N/B;y′=1,2,…,N/B。然后将Block1中变换后的第一块的像素点分布在Block2中每一块的第一个位置上,将Block1中变换后的第二块的像素点分布在Block2中每一块的第二个位置上,依此类推,直到Block1最后一块的所有像素点分布在Block2中每块的最后一个位置上,该过程由式(12)实现。
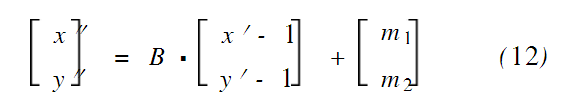
式中(m1,m2)为图像F′xy分块矩阵的块位置坐标;x″,y″为加密后图像F″xy的像素点的横纵坐标。至此完成了对图像的位置置乱。
(2)灰度置乱
首先取出位置置乱后的图像F″xy第一列像素点的灰度值,对其进行N维Arnold变换,即
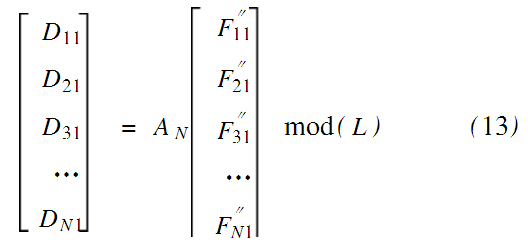
其中L是图像的灰度级,将变换后的列向量放入到密图D的最后一列上,然后取出图像的第二列像素点的灰度值如上做N维的Arnold变换,将结果放入密图的倒数第二列,依此类推,直到将图像的最后一列变换后结果放入到密图的第一列,至此完成了对图像灰度值的一次列置乱。灰度值的行置乱方法与此类似,首先取出列置乱后图像D的第一行像素点的灰度值,对其转置向量做如上Arnold变换,即:

然后将变换结果放入到密图D′的最后一行,依此类推,直到将图像的最后一行像素点的灰度值置乱变换后的结果放入到密图D′的第一行,至此完成对图像灰度值的一次行置乱。可以通过多次行和列的置乱迭代得到较好的加密图像。对于扩展的N维空间Arnold变换其周期计算要复杂得多,而且由于图像不同行不同列可能的灰度值有不同的组合排列,这导致要恢复原始图像需要完成的变换次数很大,而且难以确定,给破译造成了困难。
(3)密钥设计
本算法有3个密钥,将产生混沌序列的初始值K1和K2作为密钥,K1和K2的取值范围为(0,1)。设K3是一个12位的十进制数,如K3=12305678912表示n1=123,n2=056,n3=789,n4=123,即图像位置置乱时整体变换迭代次数为123次,各分块变换迭代次数为56次,图像灰度置乱中行变换迭代次数为789次,列迭代次数为123次。
2、加密算法的步骤
设Fxy是一个N阶的正方形图像,其中x=1,2,3,…,N,y=1,2,3,…,N,则利用该算法对图像Fxy进行文件加密的具体步骤如下:
(1)利用logistic混沌映射产生Arnold变换矩阵的参数a,b的序列,对整个图像做矩阵参数a=a0,b=b0的Arnold变换,并迭代n1次产生图像F′xy;
(2)将图像F′xy分成B×B块,将位置置乱后的密图F″xy分成N2/B2块,每块有B×B个点,取出图像F′xy第一块中的各像素点对应放入矩阵partimage中,对图像块partimage做参数=a1,b=b1的Arnold变换,迭代n2次产生图像块lastpart,并将lastpart中的点依次放入密图F″xy中每个图像块的第一个像素点的位置;
(3)取出图像F′xy第二块中的各像素点对应放入矩阵partimage中,对partimage做矩阵参数a=a2,b=b2的Arnold变换,迭代n2次产生图像块lastpart,并将lastpart中的点依次放入密图F″xy中每个图像块的第二个像素点的位置;
(4)重复步骤3的操作,直到将F′xy中最后一块的所有像素点分布在F″xy中每块的最后一个位置上,至此完成了图像位置置乱过程,得到位置置乱密图F″xy。
(5)对位置置乱后图像F″xy做灰度值的列置乱迭代n3次,得到图像D。然后对列置乱后图像D做灰度值的行置乱迭代n4次。
解密算法与加密算法密钥相同,利用Arnold变换的周期性,以及矩阵除法可实现图像的解密。
小知识之Arnold变换
Arnold变换是一种常用的图像置乱技术。











