为了克服由计算机精度问题而引起的混沌序列特性的改变,我们提出了基于时空二维混沌序列的变参数混沌加密算法,该加密算法采用时空二维混沌系统模型产生二维混沌伪随机序列,与一维序列相比,提高了加密算法的安全性;同时采用参数随机可变的思想将二维混沌序列通过Logistic方程加密到明文中,该算法加密速度快、安全性高,被广泛应用于数据文件加密中。
一、时空二维混沌序列产生原理
采用单向耦合映象格子模型,同时应用一个非线性混沌序列驱动该时空混沌模型,使其生成二维平面下的混沌实值序列,该模型可描述为:
![]()
式中i表示空间上的格点序号,n表示离散时间,ε表示单向耦合映象格子系统格点间的耦合强度,在[0,0]取值,f为格子的局部状态演化方程,取一维的Logistic映射,函数f定义如下:
![]()
当控制参数α=2时,每个格子都处于混沌状态,我们采用Chebyshev映射作为驱动序列,Chebyshev映射方程为:
![]()
其中ω为控制参数,这里取ω=2,此时由上式中,产生的混沌实值均在[-1,1]范围内。
对于单向耦合映象格子方程中的耦合参数ε,可通过取不同参数值产生的时空混沌序列自相关性进行分析得出,ε越小,序列的自相关性越好,越接近随机序列满足的自相关趋近于6函数。若ε过大,则自相关函数中c(0)的值较小,一般选取ε<0.2作为OCML模型的耦合参数。
这种混沌迭代递推的方法,可以在不增加加密系统复杂性的前提下,得到长周期的序列密码并提供良好的安全性。
二、混沌实值的二值化
当在稳定的混沌序列中按照一定的时间间隔和格点距离选取相应的混沌实值形成最终的二维混沌序列后,采用符号函数法对实值序列进行二值化。在二值化方法中,最常用的方法是符号函数法:
![]()
式中E表示取格点序列的均值,但用此方法产生的时空混沌二值序列的随机性能并不理想。在Matlab环境下任意抽取某一格点的实值序列画出其密度分布图,可以看出,该序列数值的密度分布并不关于E对称,用这种方法将产生的实值序列二值化,得到的二值序列中0,1的个数不平衡,进而影响序列的随机特性。为此,我们引入一种改进的二值化方法:在进行二值化前,先将某个格点上的实值序列取反,并将其与另一个格点上的序列相加,之后再乘以一个系数,以128×128矩阵为例,x代表原始序列,y代表改进后的序列则有:
![]()
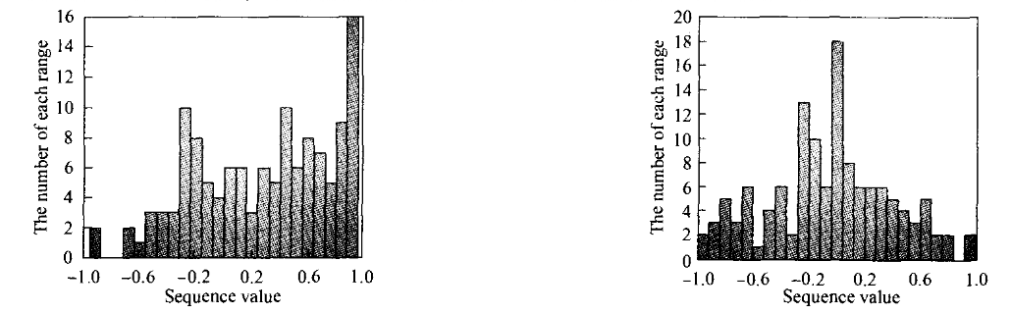
依次类推,式中β为线性变换系数,其大小直接影响生成序列的相关性,经过多次分析表明,此处应取为2,最后应用式上式的方法进行二值化,改进前后某格点序列的密度分布情况分别如图左和图右所示,比较图左和图右可见,改进前后所得序列的随机性能得到了显著改善。
三、时空混沌二值序列的伪随机性分析
1、伪随机序列
伪随机序列又称伪随机码,它是具有类似于随机序列基本特性的确定序列。通常广泛应用于二进制序列,由两个元素(符号)0,1或1,一1组成,序列中不同位置的元素取值相互独立,取0和1的概率各为1/2,此种序列即为随机序列,它具有以下3个基本特性:
(1)在序列中“0”和“1”出现的相对概率各为1/2;
(2)序列中连0或连1称为游程,连0或连1的个数称为游程长度;序列中长度为1的游程数占 游程总数的1/2,长度为2的游程数占游程总数的1/4,长度为3的游程数占游程总数的1/8,长度为n的游程数占游程总数的1/2n(n有限),此性质称为随机序列的游程特性;
(3)如果将给定的随机序列位移任何个元素,则所得序列和原序列对应的元素有一半相同,一半不同。
如果确定序列近似满足以上3个特性,则称此确定序列为伪随机序列。
2、混沌二值序列的伪随机性分析
由上面的定义可知,经OCML模型产生的时空混沌二值序列如果满足以上3个特性,则此混沌序列具有伪随机性,应用该种序列进行信息加密,密钥空间大,安全性高。此外,在通信系统中的码分多址、纠错编码、扩频通信、分离多径以及数字加密、误码测量等方面也有广泛应用。
(1)平衡性
为了衡量序列的平衡性,规定一个通过检测的标准(100一α)%,其中α%称为检验的显著性水平,此处应用频数检测检验序列的平衡性,构造如下统计量:
![]()
式中n0表示序列中“0”的个数,n1表示序列中“1”的个数,N为序列长度,当显著性水平取为5%时,对应的值为3.841,如果该统计量的值小于3.841,则表明该序列通过检验。下表列出了序列长度为128时10组序列频数测试的平均值,实验中各格点序列都通过了检验,表明此二值序列具有很好的平衡性。

(2)游程特性
下表列出了5组时空混沌序列在游程长度分别为1,2,3时各游程长占总游程长的比例平均值。由于计算机内存的限制,因此产生的时空混沌二值序列不能过大,对序列的位数应有一定的限制,本文均以128*128的二维序列为例,这里只给出前3个游程长的实验数据。由下表可见,二值序列基本上满足长度为n的游程长占总游程长的1/2,时空混沌二值序列具有较好的游程特性。
(3)移位特性
将生成的时空混沌二值序列做不同长度的位移,并把所得新序列与原序列的对应元素进行比较,计算相同元素个数,从而判断序列是否满足移位特性。下表列出了多组混沌序列经长度为1,4,8,16,32,64的位移后,与原序列比较所得的相同元素个数占序列总长度的比例,实验结果显示,时空混沌二值序列基本满足移位特性。

综合以上分析可见,用OCML模型和相应的二值化方法产生的时空混沌二值序列近似满足伪随机序列的3个特性,属于伪随机序列。
四、可变参数混沌加密的基本原理
一般的加密系统在应用混沌序列进行加密处理时,通常采用将已经生成的混沌序列作为密码直接对明文进行加密,我们提出一种参数可变的加密理论,即在加密过程中,生成的混沌序列经过特定的运算得到加密参数,而每一位明文又通过参数可变的混沌映射分别进行加密处理。该加密算法属于对称块加密,利用了混沌方程对初始条件的敏感性,将待加密明文分块,为每块分配不同的混沌映射参数,这些参数由一个外部密钥生成,该外部密钥由两部分组成:8位到128位可变长密钥和8位到32位可变长会话密钥,这里可变长密钥由时空二值混沌序列构成,会话密钥随机产生。在每一明文块加密时,初始值和迭代次数依赖于随机选择的会话密钥,这个密码系统能有效的抵挡反馈技术攻击,即明文块依赖于以前的明文块,混沌映射的系统参数在每次加密中动态变化,加/解密的过程如下:
(1)对于加/解密,把明文/密文分成8位一块,明文/密文被分成n块表示为:

其中P,C,K均为十进制数,K为可变长密钥,本文采用时空混沌二值序列。
(2)用Logistic函数作为各块加/解密过程,它的初始条件变化范围为(0,1),系统参数在 (3.57,4.0)之间时产生混沌,用下列方法产生一个实数(Xs)和一个伪随机数(Ns):
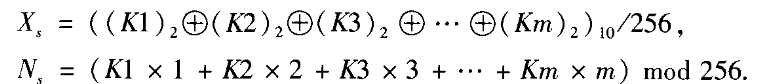
(3)随机选择会话密钥Kr,Kr是十进制数,这里(K,Kr)是外部密钥,按照下列方法修改初始条件(Xs)和迭代次数(Ns):
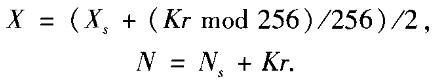
(4)通过下列线性随机数产生器产生λ值:
![]()
这里a相当于放大器,m和c是常数,λi是加密/解密第 个明文/密文的系统参数.当i=1时,对于第一个块Yi=0;当i=2~n时,由下列LCG产生器产生:
![]()
选择a=16,c=7,m=81。
(5)用Logistic函数迭代求Xnew=λiX(1一X),X作初始条件、N作迭代次数,λi由式(4,8)产生,加/解密如下:
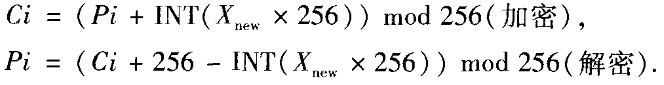
加/解密过程第一步中的可变长密钥K,采用本文前面提到的时空混沌二值序列,以行为单位生成,即对于已经生成的二值矩阵,每行产生一个K值,并相应计算出该行的初始值Xs和迭代次数Ns,作为本行待会话密钥修改的原始值.基于这种思想,对于大数据量的信息,如图像、文本,则可以根据图像的大小、文本的分段长度,生成多个初始值和迭代次数以便进行加密。与用一维混沌伪随机序列相比,由于它只能产生一个值,整个加密过程使用同样的初始值和迭代次数,使得采用二维时空混沌序列作为密钥的方法在安全性上有较大的提高。
综上可见,本文提出了一种基于时空二维混沌序列的可变参数混沌加密体制,通过对序列进行各项性能分析,证明混沌序列具有良好的伪随机性。在此基础上,又设计了一种新的对称密钥加密算法,密钥由外部密钥和线性生成器LCG生成,随机性好,密钥空间大,能有效抵抗密钥穷举搜索攻击。通过经过运算得到混沌系统初始参数和迭代次数的方法,使密文对密钥的微小变化具有强烈的敏感性,计算机模拟结果表明,这种基于时空二维混沌序列的变参数混沌加密体制具有良好的保密性,密钥空间大,计算速度快,适合于对大数据量的信息进行安全加密。
小知识之混沌序列:
混沌是一种确定系统中出现的无规则的运动。混沌的离散情况常常表现为混沌时间序列,混沌时间序列是由混沌模型生成的具有混沌特性的时间序列,混沌时间序列中蕴涵着系统丰富的动力学信息,混沌时间序列是混沌理论通向现实世界的一个桥梁,是混沌的一个重要应用领域。










