数字签名用于鉴定签名人的身份以及对一项电子数据内容的认可。它还能验证出文件的原文在传输过程中有无变动,确保传输电子文件的完整性、真实性和不可抵赖性。下面我将给大家介绍一种基于椭圆曲线加密算法的数字签名技术。
基于椭圆曲线加密算法的数字签名
1、基于椭圆曲线加密算法数字签名的原理
(1)生成密钥对
首先,需要确定加密算法的公钥与私钥。选择一条椭圆曲线E(a,b,p值给定),在E上选取一个周期很大的点P=(Xp,Yp),它的周期为一个很大的素数n。在椭圆曲线密码体制中,具体的曲线E及点P和它的周期n都是公开信息。给定参数(p,E,P,n)以后,选择d∈R[1,n-1]。计算Q=dP,返回(Q,d),其中,Q为公钥,d为私钥。
(2)加密算法
确定了椭圆曲线加密算法的公钥与私钥以后,就可以进行加密了。加密算法如下:
首先,确定参数组(p,E,P,n),公钥Q,明文m;然后,将明文m表示为椭圆曲线E上的点M;选择k∈R[1,n-1],计算C1=kP,C2=M+kQ。(C1,C2)就是明文文件加密后的密文。
(3)解密算法
收到密文文件以后,可以对密文进行解密,解密算法如下:
首先,确定参数组(p,E,P,n),私钥d,密文(C1,C2);然后,计算M=C2-dC1,并从点M中取出明文m。
2、基于椭圆曲线加密算法数字签名过程
(1)签名过程
假如现在A想给签署一份文件,为确认这份文件确实是A签署的,可以先对这份文件进行数字签名。用椭圆曲线加密算法的数字签名过程如下:
a、对明文使用HASH加密算法,得到明文的数据摘要。(大多时候,明文的信息都比较长,如果直接用椭圆曲线加密算法加密,加密的速度会比较慢,而且耗费系统资源。这时候,可使用HASH函数,使用MD5或者SHA算法生成数据摘要。这样做的优点是:输出较短,一般是128位;抗逆向攻击;抗碰撞攻击);
b、对数据摘要进行加密,使用A的私钥进行椭圆曲线算法加密,得到数据摘要的密文;
c、将明文和加密后的摘要同时进行DES加密,将密文送给B。数字签名过程,如图所示:

(2)验证过程
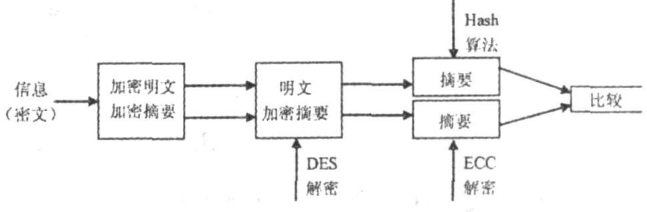
B收到A发来的密文后,为了验证密文确实是A发送的,可以对密文进行验证,验证过程如下:
a、对密文进行DES解密,得到明文和A用椭圆曲线算法机密后的摘要;
b、对明文使用HASH算法,得到明文的数据摘要;
c、使用A的公钥对A加密的数据摘要进行解密,得到数据摘要;
d、将b和c得到的数据摘要进行比较,如果相同,则说明该密文确实是A发送的,如不同,,则说明该密文不是A发送的。
小知识之椭圆曲线加密算法
椭圆曲线加密算法是一种公钥加密算法,与主流的RSA算法相比,椭圆曲线加密算法可以使用较短的密钥达到相同的安全程度。











