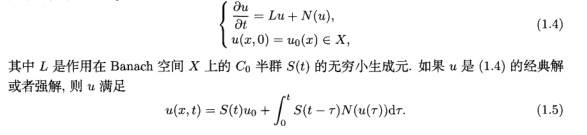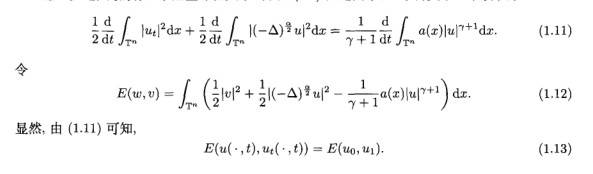1987 年,B lakley 和 R undell[3] 提出把分析数学应用到密码学,即基于偏微分方程及其反问题的理论构造热流密码体制 (heat flow cryptosystem ).他们利用关于时间不可逆的整数阶热传导方程构造一类正向计算容易但反向求逆困难的函数 (称为单向散列函数),并进一步利用伪抛物型方程的两个初边值问题构造对称密码算法.其基本思想是利用伪抛物型方程在定解条件下正、反问题的适定性实现加密、解密的操作;保密性则 由方程系数未知的条件下伪抛物型方程反问题的不适定性来保证.目前,热流密码体制所取得的成果主要集中在两个方面:基于不的偏微分方程模型构造对称密码算法;探讨各种数值方法的稳定性、效率和精度,为热流密码体制建立稳定、高效的计算格式.
1 非线性分数阶双曲型方程
我们首先考虑线性方程
定义 1.1
作用在 B anach 空间上的有界线性算子半群 s (£),0t < ∞,被称为强连续算子半群,如果 lim _+0 (t)“= 'it对任意 ∈X 都成立.作用在上的强连续有界线性算子半群也 叫做半群
接着我们给出关于一般抽象 C auchy 问题的解的存在性及爆破解的定理.设 乱= u(x ,t) 满足下列抽象 C auchy 问题:
定义 1.2
若 U0 ∈X 且 N ∈L (0, ; ).由 (1.5) 给出的函数 U ∈c ([0, ;X ) 是初值问题 (1.4) 在 [0,T 1上的温和解.
定理 1.1[ 】 设 Ⅳ 是从到的局部 Lipschitz 的非线性算子,且满足(i) llⅣ(札)lixCbd(ii~llx ),Vu ∈X ,(ii) lIN (u1)一N (u2)IIx CLip(1l~lll,ll 2l1)lI,“1一U2llx ,其中d 和ip 是关于各 自变量的非减函数.那么对于 P > 0,存在(p) > 0,使得对于任意满足 Iluo(x)P 的 uo(x)∈X ,问题 (1.4)存在唯一的温和解 ( ,t)∈c ([0,Tm 】, ).进一步地,则
定理 1.2 设 7 满足 (1.10)且 = ( )∈X ,问题 (0.1)和 (0.2)存在唯一温和解 ( )∈c ([0,T】;).进一步地,我们有以下能量守恒关系.方程 (0.1) 两边同乘以 t 再关于 X 积分,得:
利用类似于 (1.11) 的估计,我们发现方程 (0.2) 的温和解是可以全局存在的,对方程 (0,1),我们有以下关于爆破解的结果.
定理 1.3若 Eo = E (u0(.),钆1(.))0,或者 E o = 0 且uou]dx > 0,则定理 1.2 中方程 (0.1) 的解会在有限时间内爆破,并且
注 1.1若> 0,对 0,1再附加条件,类似于文献 [7]中的讨论,同样可以得到关于爆破解的结论.注意到 (1.15) 弱于我们得到爆破解结论所依赖的条件,即 li m Ilu( )llLz( 。)∞·(1.18)
们没有找到 (1.18)成立的条件,但是我们在下面的定理中给出了 llu(t)ll~。的导数爆破条件.
注 2.1
加密系统最重要的性质在于保证 J[)(E (M ))= M ,即保证明文加密后再解密仍然是原来的明文.而我们的加密方案的生成密文是通过数值方法得到的 u (x,to),若以此 u(x,to) 求解方程 (2.1)来得出原来的初值 u( ,0),其误差取决于所使用的数值方法,有可能与真正的明文有较大的差别.为了减少这样的误差,实际的解密过程可以采用加密过程中求解方程 (0.2) 的差分格式,但迭代的方向和加密时相反,这样解密就是加密的逆过程,可以有效减少最终明文的误差,保证解密正确.
3 小结
本文分别讨论了方程 (0.2) 的解的全局存在性以及方程 (0.1) 的解的局部存在性,并给出两个关于爆破解的结论.我们指出利用方程 (0.2) 正、反问题的适定性,可以构造热流密码体制的加密算法.因为分数阶微分方程的数值算法还不成熟,特别是分数阶导数力学动力系统的计算稳定性至今还缺乏系统的分析研究,所以如何控制误差传播、构造实用的加密算法 尚有待进一步研究