针对单一混沌映射密钥空间小、易受攻击且在有限精度的系统下受限等问题及高维混沌系统计算量大的缺陷,我们提出了一种基于Logistic映射与Chebyshev映射的遥感影像加密算法。
一、基于复合混沌映射的加密算法基本原理
1、基于Logistic映射和Chebyshev映射的混沌系统
Logistic映射是一种可产生混沌的非线性系统,其模型为:
其中:0<μ≤4——分支参数,xi∈(O,1),i=O,1,2,3,…。混沌动力系统的研究工作指出,当分支系数3. 5699456<μ≤4时,则Logistic映射工作于混沌状态,也就是说,在Logistic映射的作用下由初始值xo所产生的序列{xi,i=O,1,2,3.…}是非周期、不收敛的,并对初始值非常敏感。
Chebyshev映射定义为:
式中:k-表征系统非线性强度的系数,当k≥2时,映射处于混沌状态。在方程的初值k给定情况下,方程通过迭代将生成一组混沌序列{xn,n=l,2,…)。
2、加密算法基本原理描述
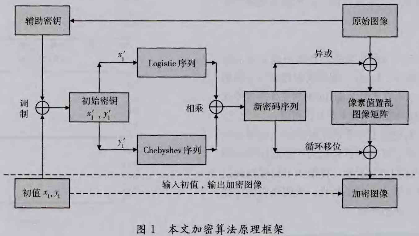
本文算法加密的基本原理为:先借助原始遥感影像产生一个辅助密钥,将辅助密钥分别与两个初始值调制产生两个初始密钥,由此初始密钥生成Logistic映射序列和基于Chebyshev映射的混沌序列,将这两个混沌序列相乘而得到新的混沌序列,并将其转化为[O,255]之间的整数密码序列。最后利用该密码序列对原始遥感影像进行像素值的异或,每生成一个密钥便可与图像像素进行异或操作,直至密钥全部产生。异或操作也进行完毕。最后随机选取一段密码序列对异或后的影像矩阵进行行列循环移位,最终得到加密图像。整个加密过程没有等待,实时性好。其原理框架如图1所示。
辅助密钥的引入使得系统的初始密钥对明文有很强的依赖性,整个算法对明文比较敏感,明文图像的任何一部分微小的变化都会引起辅助密钥的变化,进而导致初始密钥的变化,这样使得攻击者很难通过已知明文的攻击方式破泽加密图像,辅助密钥的引入还可以增大主密钥空间。
低维混沌序列很容易受到混沌模型重构方法的攻击,本文算法使用基于Logistic映射的混沌序列和基于Cheby-shev映射的混沌序列复合而得到的新混沌序列掩盖了混沌子序列的分布特性,改变了原混沌系统的动力学行为,可以有效抵制模型重构攻击算法,保密性优于通常的低维混沌序列且计算量小于高维混沌序列。
此外,常见的混沌图像加密都是单一使用像素位置或像素值置乱。本文算法结合像素值异或和像素位置循环移位置乱加密,进一步提高了算法的安全性。
二、加密与解密过程具有实现步骤
设待加密图像I为M×N×8的灰度图像,加密过程如下:
(1)初值及参数的选定。选定Logistic映射分支参数μ及初值X1和Chebyshev映射系统参数k及初值yl。
(2)生成辅助密钥。将原始图像I的所有像素值相加得到像素和Sum,并通过运算mod(SUm,256)/256得到辅助密钥Key。辅助密钥与原始图像相关t即当原始图像发生变化时,辅助密钥也会相应改变。
(3)混沌系统初始密钥的生成。将辅助密钥Key分别与初值x1、y1相乘(Key作为调制因子),得到新的系统初值x1'、y1'。
(4)基于Logistic映射与基于Chebyshev映射的混沌序列产生。设基于Logistic映射的混沌序列为L,基于Chebyshev映射的混沌序列为Hi设常数S-1000,在得到初值x1‘及给定系统参数μ的情况下,由式(1)迭代(MX
N-I+S)次得到序列(X71’X72,…,xm*n+S)。最后舍弃前S个点并将其得到的实值序列记为(ri,r2,…,rmn)。依据同样的方法可以得到基于Chebyshev映射的实值混沌序列,记为(p1,p2,…,pm*N)。
(5)新复合混沌序列的构造矿将实值序列(r1,r2,...,rMXN)和(pl,p2,…,pNWN)逐位相乘得到新的实值混沌序列,并将其转化为[o,255]之间的整数密码序列,记为(Z1,z2,…,Zm*n)。
(6)像素值异或置乱。将整数密码序列(Z1,z2,…,Zm*n)与原始图像Am*n逐行进行异或得到加密图像矩阵Bm*n。
(7)像素位置循环移位置乱。随机选取整数密码序列(Z1,z2,…,Zm*n)中的一段长为M+N的整数密码序列(Z1’,z2',…,Zm*n'),将前M个值作为行移位值,后N个值作为列移位值对矩阵Bm*n分别进行向右和向下的行列移位。
图像解密过程为加密过程的逆过程。
三、仿真实验及讨论
—个好的加密算法,应该具有密钥敏感性、明文敏感性和低的密文相邻像素相关性等特性:下面分别进行实验验证。
1、加密实验
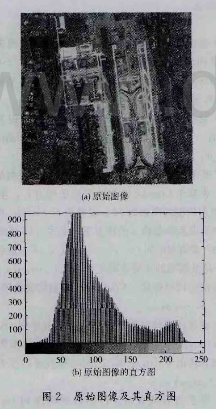
实验采用256X256×8的机场遥感灰度图像为待加密的原始图像,如图2所示。
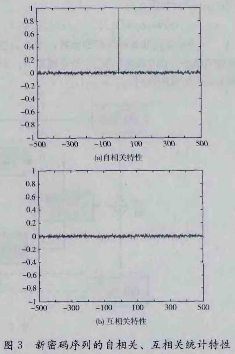
Logistic混沌映射选用分支系数μ= 3.8,初值x1=0.5,此时Logistic映射工作于混沌状态,Chebyshev混沌映射选用参数k=6,初值yi≥0.2,此时系统进入混沌。利用以上两个混沌映射产生的新密码序列,并随机抽取一段子序列将其转化为二进制序列得到其自相关、互相关特性如图3所示。由图3可以看出此二进制序列有很好的自相关和互相关特性。表明该密码序列满足平均分布,可作为加密密钥。
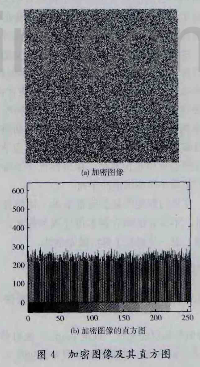
利用新密码序列对原始图像像素值和像素位置进行双重加密。加密图像及其直方图如图4所示。由图4可见,加密后图像类似白噪声,影像混乱,且其直方图均匀分布在[O,255]区间上对用置乱度衡最准则对其进行评价,置乱后置乱度可达20. 5535,质心坐标为(128. 44,128. 40),置乱后质心很接近其形心坐标(128,128),说明本文所提加密算法置乱效果很好。
2、密钥和对原始图像敏感性实验
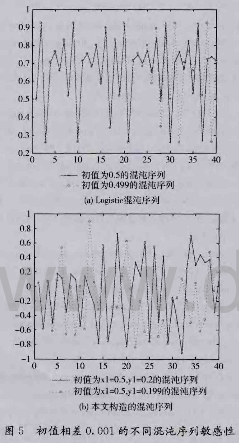
混沌序列对初值的敏感性保证了混沌加密算法对密钥的敏感性。在混沌系统中,参数和初始条件的微小变化都对混沌信号有很大影响。如图5 (a)所示,初始值x0仅相差0. 001的两个Logistic混沌序列在经过约20次迭代后迅速分离,成为两个不相关的序列,可见混沌序列对初值敏感,且易于大量产生,适合图像置乱加密。图5 (b)是本文算法构造的混沌序列的初始值仅相差0. 001时的迭代情况。
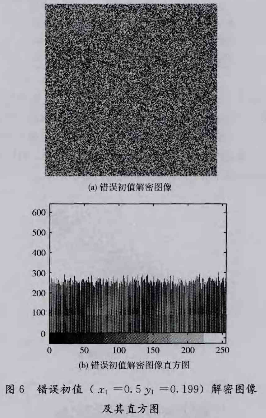
由图可见,新密码序列迭代3次后就出现明显分岔,表明本文所构造的复合混沌序列对初始值十分敏感。采用错误的密钥初值乱x1=0.5,Y1=O.199对置乱后的遥感影像进行混沌解密,得到的遥感影像及其直方图如图6所示,解密图像杂乱不堪,直方图分布均匀,可见本文所提加密算法对初值非常敏感。
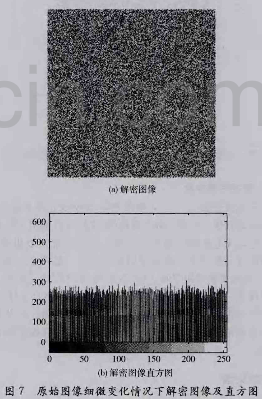
用相同密钥对相差1像素不同的两个原始图像加密,并在不改变密钥的情况下解密,结果如图7所示。由图7可知,加密图像对原始图像非常敏感,说明该算法具有很好的抵抗差分攻击的能力。
3、相邻像素相关性
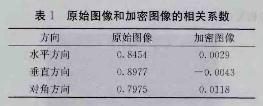
为了验证加密图像相邻像素之间的相关性,分别从水平、垂直和对角方向随机选取1000对相邻像素计算相邻像素的相关系数:如表1所示。
由表1可知,原始图像相邻像素的相关系数是高度相关的,相关系数接近于1。而加密图像相邻像素的相关系数接近于O,相邻像素已经基本没有了相关性,也就是说原始图像的统计特征被扩散到了随机的加密图像中,原始图像和加密图像水平方向像素的相关性如图8所示。
4、密钥空间分析
将系统初值x1,yl,辅助密钥Key及系统参数μ,k作为最初密钥,采用小数点精确到15位(当密钥变化小于10-15时,认为密钥没有发生变化,可以正常恢复出图像)的双精度实数表示,则密钥空间为1075。是单个一维Lo-gistic混沌系统密钥空间1015×1015)的1045倍。此外,在对图像进行循环移位置乱时还可以选择(MX N) /(M+N)个不同的密码子序列,这也可以作为一个密钥。所以该加密算法密钥空间大,安全性很好,可以有效抵抗密钥的穷举攻击。
小知识之遥感
遥感是指非接触的,远距离的探测技术。