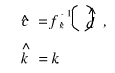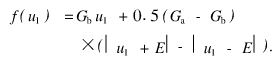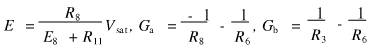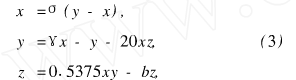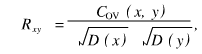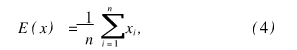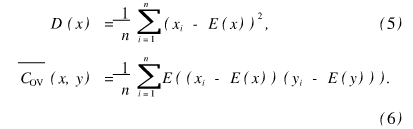随着实时快捷的信息交流与信息安全之间矛盾的日益突出,混沌通信和混沌加密技术成为国际电子通信领域的一个热门课题,并在密码学领域内日益显示出一定的优越性和潜在的生命力。为此,我们提出了一种物理混沌图像加密系统。
一、物理混沌和算法混沌的基本概念
由一个混沌系统产生的混沌吸引子可分为算法混沌和物理混沌两类,利用没有随机扰动的数值计算装置(如计算机)所产生的混沌吸引子属于算法混沌,而利用具有随机扰动的物理实现装置(如模拟电路)所产生的混沌吸引子属于物理混沌。由于随机扰动的存在而初始条件随时改变,物理混沌吸引子是不可预测的。对于算法混沌,由于没有随机扰动,其轨道完全取决于初值,因而是可预测的。因此,基于物理混沌的保密通信系统是理想的具有高安全性的通信系统.而算法混沌由于具有可复制、类噪声的优点广泛应用于混沌研究中;但将其用于保密通信则系统安全性相对较差,这是后者明显的不足。
值得指出的是,对于物理混沌,实际波形的测量值有一定的误差,但混沌波形的近似仍然是混沌的。这种有限精度徽应与产生伪混沌序列的数字仿真系统具有实质性的不同。前者没有改变原有的初值复杂性,其影响相应于连续频谱的局部改变,而后者则因丧失初值复杂性必然是可预测的。
二、混合加密方案原理
初值敏感性、类随机性和不可预测性是混沌系统的主要特征,也是其被应用于密码学的最根本原因,混沌加密系统的主要优点是可以利用混沌信号的不可预测性,主要缺点是没有解决密钥空间的设计问题:常规加密系统的主要优点在于具有成熟的密钥空间设计技术,而且其安全性较容易评估;而主要缺点是明文密文对的唯一对应而有可能被破译。因此由混沌加密器与常规加密器相结合构成的混合加密系统,使两种加密器的优点可以互补,整个系统的抗攻击能力明显高于其中的任一加密器。
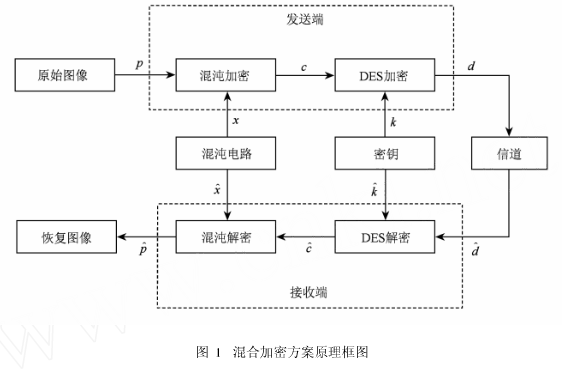
基于物理混沌的混合加密方案原理如图l所示。
DES是一种较为典型的分组密码算法,使用一个56位的密钥以及附加的8位奇偶校验位,产生最大64位的密钥大小,使用Feistel技术,将加密的信息块分成各32位的两组,使用子密钥对其中一半应用循环功能,然后将其输出与另一半进行异或运算;接着交换这两半,这是一个迭代的分组密码,共进行16次循环。
混合加密算法的主要步骤如下:
1)混沌电路产生的连续信号经采样得到序列xi,xi经过一定变换得到xj,由xj构成的z对原始信息p加密,得到混沌加密密文C。
2)密文c经过常规加密技术DES在密钥k加密下得到加密密文d。
其中fk()表示经密钥七加密下密文c到d的映射。
3)将加密密文d经信道传送,接收端收到信号d。
4)接收端首先对d进行解密,在密钥k解密下得到解密密文c。
除了唯密文攻击之外,常规加密算法的所有已知攻击方法洳直接针对DES的差分分析和线性分析的基本条件是某些唯一对应的明文密文对,由于采用硬件实现的混沌系统,前级密钥信号x是不可预测的,因而其输出c是随机变化的,故不存在唯一对应的明文密文对。这是前级的优点。混合级联加密系统的后级佯规加密器J因其输入不可预测而不可能有唯一对应的明文密文对输入输出对j,其关键在于由物理混沌产生的x不能用算法描述,这样,上述的已知攻击方法在原理上不可能击破混合加密系统中的常规加密器。由此可见,前级优点弥补了后级的弱点,而显著增强了后级的安全性。在上述系统的后级不可击破的情况下,要获得其输入信号c是不可能的,而目前已知的利用频谱分析、系统识别等破译方法对于前级的攻击也就无能为力。因此,这一方案的安全性能容易评估,不存在比唯密文攻击更加有效的破译方法。
三、混沌信号的产生
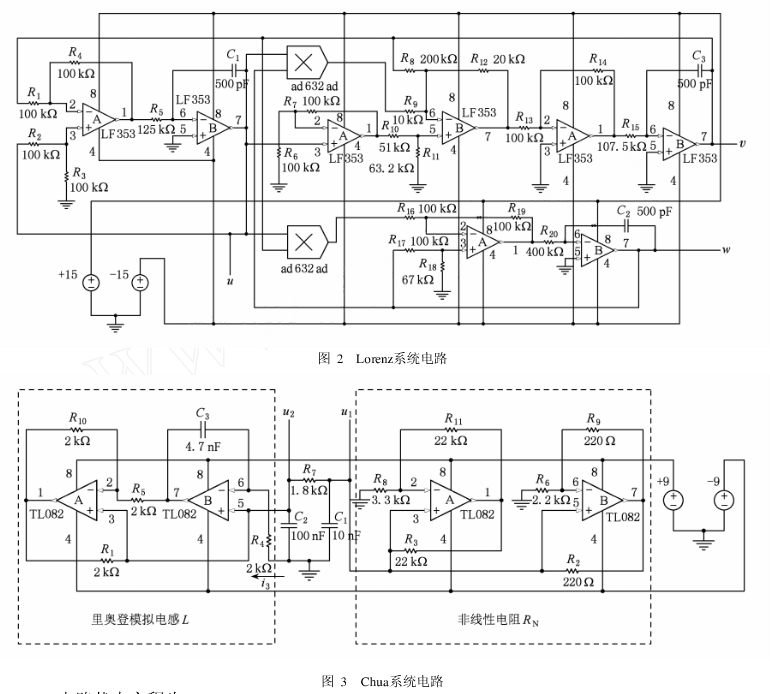
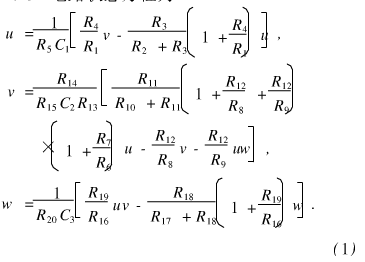
本实验应用的混沌信号分别为Loienz物理混沌、Chua物理混沌和Lorenz算法混沌。Lorenz和Chua电路分别如图2和图3所示,基波频率均设计为3 kHz参数选择已在图中标示。
Chua电路状态方程为:
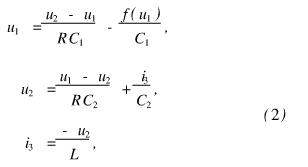
其中非线性电阻RN的特性可表示为:
分段线性转折点电压E及斜率Ga,Gb与元件参数关系可表示为:
其中,Vsat为运放的输出饱和电压。
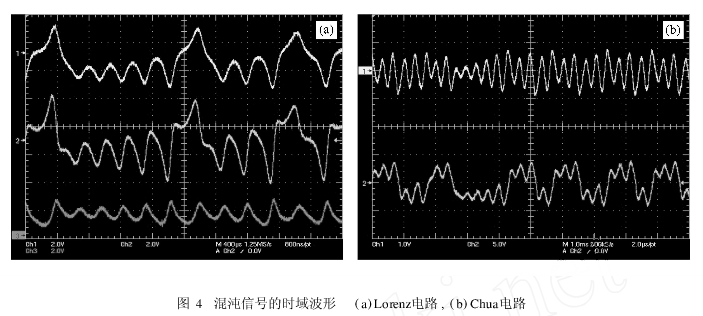
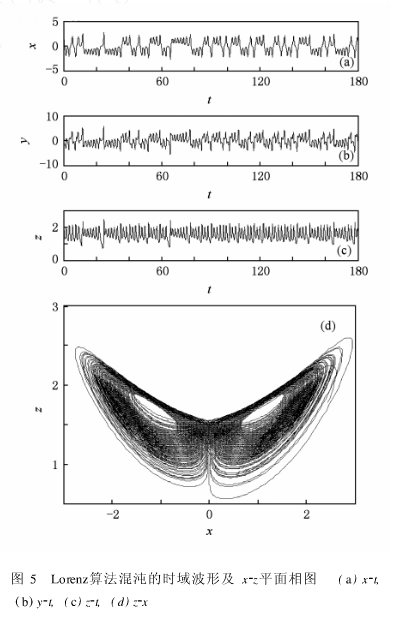
Lo renz电路和Chua电路输出电压的时域波形分别如图4(a)和(b)所示,采样频率均取500 kHz。
Lorenz算法混沌的状态方程由物理混沌电路方程归一化得到,
其中σ=1. 72,γ=34. 31,b=0. 4312,系统时域波形及x-z平面相图如图5所示。
四、算法仿真结果
先对涉及的多个不同加密系统予以说明。A和B级联的加密系统以“A书’标识,如Lo renz物理混沌和DES级联的加密系统以物理Lorenz-DES标识,算法Lo renz-D ES、物理Lorenz算法Lorenz和物理Chua-DES意义类同,单级加密系统分别以单级DES加密、单级物理Lorenz加密单级算法Lorenz加密标识,其中单级物理Lorenz加密和单级算法Lorenz加密,分别选用与物理Lorenz-DES’和算法Lorenz-DES中第一级相同的加密算法和参数。
仿真过程采用Matlab 7.5实现并选取160×160的Lena灰度图作为加密图像,如图6(a)所示。
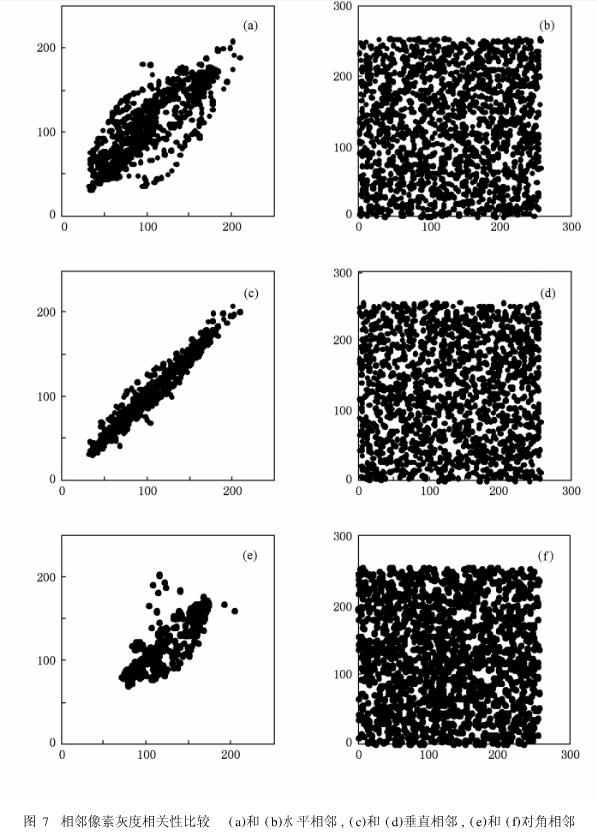
混沌序列由图2所示Lo renz混沌电路产生,各加密结果如图6 (b)和(c)所示。DES加密密钥为“样(.5+a/&”,正确解密结果如图6(d)所示。若解密密钥作微小变动为“#).5+a/&’讨,解密结果如图6(e)所示。即使解密密钥微小变动都不能得到正确的解密结果,说明该算法对密钥具有较高的敏感度,图6(f)为单级DES加密图像,随机选取1600个像素点,分别画出物理Lo renz-D ES加密方案中原始图像和加密图像的水平相邻、垂直相邻和对角相邻像素的灰度关系,如图7所示。从图7可以看出,加密前后图像的相邻像素相关性大大降低。
以上仿真结果一方面验证了算法的正确性,另一方面表明基于该方案的加密系统具有良好的扩散和混淆特性。
1、物理Lorenz-D ES和单级加密特性的比较
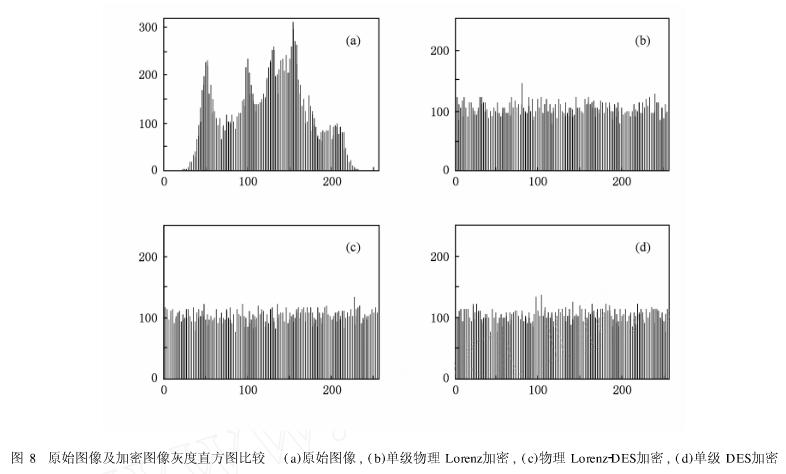
(1)灰度分布直方图
图8所示为原始图像和各加密图像的灰度直方图。
直观上,图(c)灰度均匀性略优于图8(b)和(d),说明两级级联的加密系统可以改善密文的灰度统计特性。
(2)相邻像素相关系数
选择部分像素进行相邻像素相关系数比较,仅能部分说明加密算法扩散和混淆的程度,为进行定量比较,本文选择计算整幅图像相关系。
COv (x,y)表示五),的协方差,定义为:
Rxy表示xy的相关系数,定义为:
式中E(x)表示工的数学期望,D (x)表示x的方差,在实际运算中,可通过下式进行:
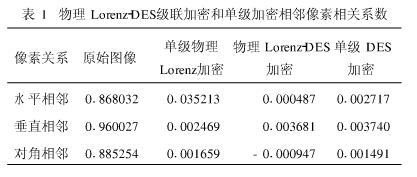
物理LorenzDES和单级加密的相邻像素相关系数见表1。
表1中数据说明:原始图像三个方向相关系数值从定量的角度反映了图7中相邻像素的相关程度,验证了算法的正确性.级联加密系统相邻像素相关性与单级加密相比总体上有明显改善。从相邻像素相关系数这一指标来看,单级DES加密和单级物理Lorenz混沌加密具有相似的特性,但加密速度却相差甚远.单级DES加密耗时约为2209 s,而单级物理Lorenz混沌加密却仅需约0.5 s级联加密时间即为两者之和。因此,当图像加密实时性要求不高时采取物理混沌-DES级联的加密方案是合适的,可以充分利用两种系统的优点,获得较高的安全性。若需要兼顾加解密速度,则宜考虑以算法混沌代替DES,即采取物理混沌算法混沌级联的加密系统,其中算法混沌系统主要任务在于形成一定的密钥空间。
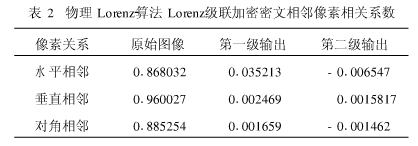
表2中列出了基于Lorenz系统的物理Lo renz-算法Lo renz级联加密各级密文的相关系数。由此可以看出,该级联加密系统同样可以改善密文相关性特性,但逊于物理Lo renz-D ES加密方案,而加密速度却获得了极大改善,物理Lo renz算法Lo renz级联加密系统耗时仅约1s后一种方案也因其实时性好而具有应用前景。
从以上分析可以得出,混沌加密和常规加密级联的主要原因在于两种不同加密体制的优势互补,密文特性总体也有明显改善。
2、不可预测性强弱不同的混沌信号对图像密文特性的影响
同一系统的物理混沌不可预测性强于算法混沌;Lorenz系统不可预测性强于Chua系统。为了研究不可预测性强弱不同的混沌信号对密文特性的影响,我们选择改变图1方案中的混沌系统,并用相邻像素相关系数作为指标来分析比较密文特性的不同。
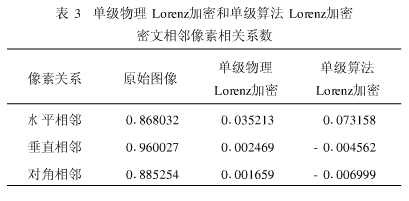
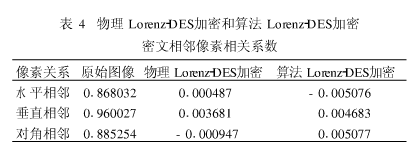
首先比较物理Lo renz-D ES加密和算法Lo renz-DES加密的密文特性。将物理Lorenz加密系统的混沌信号改为由Lo renz算法混沌产生,得到算法Lo renz加密系统。单级物理Lorenz加密和单级算法Lo renz加密密文的各相关系数比较见表3,物理Lo renz-D ES加密和算法Lo renz-D ES加密的密文相关系数比较见表4。
从表3和表4可以看出:经单级Lo renz算法混沌加密后的图像各方向相关系数均大于物理混沌加密的情形;级联DES后算法Lo renz-D ES加密系统密文各相关系数同样明显大于物理Lo renz-D ES的情形。重复进行不同基频的多组实验或者将系统换为Chua系统,也可得出与此一致的结论。
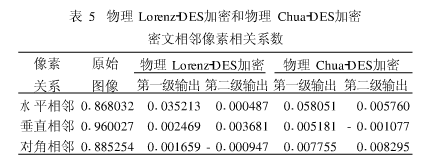
其次比较物理Lo renz-D ES加密和物理Chua-DES加密特性,加密方案和算法仿真的相关参数与物理Lo tenz-D ES相同。Chua混沌序列由图3所示的Chua电路产生。表5分别列出了两种加密系统各级密文相邻像素相关系数。
表5表明,单级物理LoIenz加密密文相关系数均小于单级Chua加密相关系统,且总体上物理Lo renz-D ES加密密文特性明显优于物理Chua-DES系统加密密文特性。
综合以上分析可知,不可预测性越强的混沌信号用于加密时其密文相关性越弱,反之亦然。
小知识之混沌现象
混沌现象是指发生在确定性系统中的貌似随机的不规则运动,一个确定性理论描述的系统,其行为却表现为不确定性一不可重复、不可预测,这就是混沌现象。