针时图像加密算法容易被破解、效率低等问题,提出了一种基于广义2D-Arnold映射和超混沌的图像文件加密算法。这种难过图像文件加密算法可以确保在安全可靠的前提下,明显提高效率。
一、图像的置乱过程
1、广义2D-Arnold映射
广义2D-Arnold映射是一个2维保面积的一一映射,单位矩阵的任一点唯一地变换到单位矩阵内的另一点,可逆映射,没有吸引子,非常适合图像置乱。实际上,Amold映射包括拉伸和折叠两个过程,乘以矩阵C,x,y变大,相当于拉伸,取模,使x,y又回到单位矩阵内,相当于折叠。如此循环往复,最终达到混叠的目的。映射方程为:
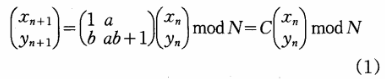
式中a,b,N为正整数,参数a,b以N为周期,要求a,b∈N。若初始值x0,yo为正整数,则xn,y为(x=O,1,2,…)也均为正整数。可通过将图像的像素坐标或灰度值作为初始值进行迭代来实现图像的置乱。对于图像内原来相邻的两点如(xn,yn)和(xn+1,yn+1),其像素坐标经广义猫映射迭代几次后不再相邻;具有均匀概率分布的猫映射还可以保证经过一定次数的灰度值迭代后,原图像的灰度直方图由具有特定的统计规律改变为呈均匀分布,从而达到图像保密的目的。
2、原始图像的置乱过程
假设原始明文图像大小为MxN。置乱过程的步骤如下:
(1)读入原始明文图像,如果M>N,将原始明文图像的第一列数据复制到N+1列,第二列数据复制到第N+2列,依此类推,直到满足M=N为止,得到正方形图像,反之一样。
(2)使用2D-Amold映射置乱像素点位置,通过式(2)对调整后的正方形图像进行置换。2D-Arnold映射参数a和b和置乱轮数优为密钥,2D-Arnold映射矩阵的各个数据分别为A11=1,A12=a,A12=b,A22=ab+1,从而保证2D-Arnold映射矩阵的行列式|C|=1。
![]()
二、图像的扩散过程
1、超混沌系统模型
超混沌系统的动力学方程如下:
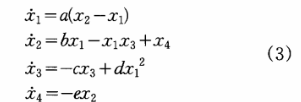
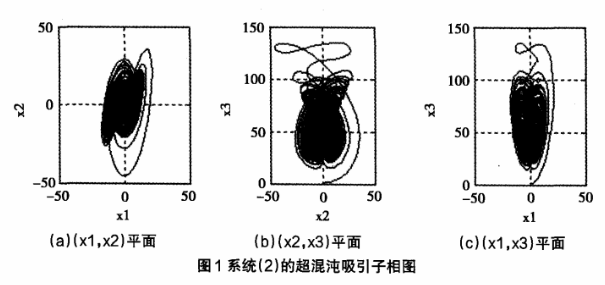
式中,a,b,c,d,e为系统参数,当a=10,b=45,c=2.5,d=4,e=5时,系统存在超混沌吸引子,表现为超混沌运动。在Matlab7.O的环境下对系统进行仿真,得到超混沌系统仿真结果,如图1所示。系统具有更复杂的相空间,表现出更加复杂的动力学性质,产生的混沌序列具有更好地随机性,用它设计密钥更加安全。
2、超混沌密钥序列的生成
使用超混沌方程式(2)生成超混沌序列的步骤如下:
(1)超混沌系统取四个初值x,y,z,w,预迭代N次,得到xo,Yo,z0,wo及迭代次数No,将其作为初始密钥。
(2)对超混沌系统以初始值xo,Yo,z0,wo迭代L/4次,得到四组超混沌序列{Xk,yk,Zk,wk},(l≤k<L,L =MAX(M,N)xMAX(M,N))。
(3)初始化—个空序列Aa设M=mod(X1,Yi,ZI,wl,2),若m=0,将(X1,Yi,Z1,WI)加入序列A,若m=1,将(yl,Xi,Z1,Wl)加入序列A,若m=2,将(Z1,Xl,Yi,W1)加入序列A。
(4)初始化—个空序列Bo设n=mod(xk+yk+Zk+wk,2),若n=0,将(W1,XI,Yi,Zl)加入序列B,若m=1,将(Z1,xi,yl,w1)加入序列B,若m=2,将(z1,wl,Yi,XI)加入序列B。
重复执行步骤(3)和(4),生成两个长度为L的原始混沌序列A和B。
按照变换式:

对混沌序列进行改造,得到混沌密钥序列k1,k2。k1i(i)∈[O,255],k2i∈[O,255]。
式中,floor(x)表示取不大于x的最大整数;mod(x,y)表示取x除以y所得的余数。
3、图像的扩散操作
图象扩散操作由以上两个混沌系统产生的密钥对图象进行两论扩散操作。在扩散过程中使用混沌系统产生的两种密钥交替加密,并引入密钥扩散机制,使明文、密文、密钥之间的关系更加复杂。把得到的超混沌序列按照置换的图像矩阵的大小变换成矩阵形式,称之为灰度矩阵H1和H20经过这样的变换,要扩散的图像矩阵就和灰度矩阵具有同样地大小,便于进一步处理。
第一轮扩散加密过程如下:

第二轮扩散加密过程如下:

其中,D表示置乱后图像矩阵,E表示加密后图像矩阵,Eo.o,EM.N为加密第一个明文像素时的初始密钥,E0.∈[O,255],EM.N∈[0,255],H1和H2为混沌灰度矩阵。
在以上的算法中,Eo.o为a和6进行二进制“位异或”运算;mod(a,b)为“盘除以b”得到的余数。
由上述的加密方法看到,图像的扩散过程由两个混沌灰度矩阵共同作用,扩散过程不仅与明文相关,也与密文相关,同时引进了非线性的“取模”操作,因此,攻击者想要破译出最终的密钥的可能性是非常小的。
三、图像的解密过程
解密过程是加密的逆过程,首先,利用初始密钥生成的超混沌密钥岛和k2,把得到的超混沌序列按照置换的图像矩阵的大小变换成灰度矩阵H1和H2,实现置乱图像的复原。
反置乱过程如下:
反置乱过程是置乱过程的逆运算,利用相同密钥的2D-Arnold映射的逆矩阵进行像素点位置的复原,逆矩阵如式(1O)所示。
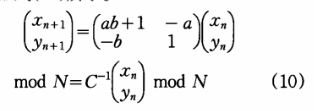
四、实验仿真
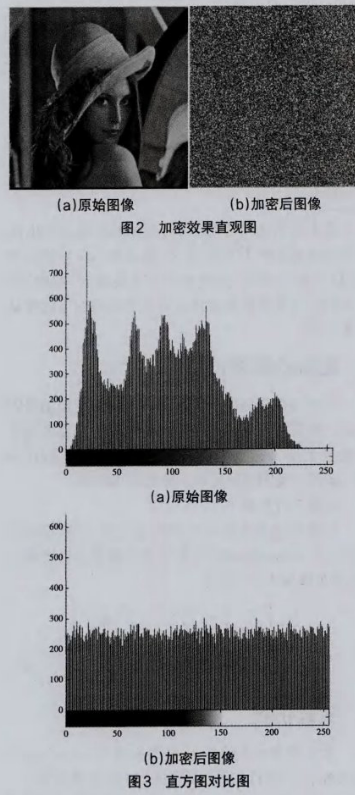
本文使用256位的经典测试图像lena.bmp在Matlab7.O下进行仿真,设定式(1)的系统参数a=M-2,b=M-4,m=16,保证ab都是小于M的正整数,而且密钥a,b与图像的大小相关。式(2)的系统参数a=10,b=45,c=2.5,d=4,e=5时,系统是超混沌的,超混沌系统初值取为(0.22,0.57,1.O,0.30),微分方程的求解的时间步长为0.001,预迭代次数No =1000,初始密钥Eo.o=102,EM.N=28.Lena原图像如图2(a)所示,加密后的图像如图2(b)所示。比较原始图像和加密图像后发现,二者存在巨大差别,加密图像已经完全隐藏了原始图像。原始图像的直方图和加密后的图像的直方图如图3所示,原始lena图像的像素值分布非常不均匀,加密后的直方图表明像素值在[0,255]内呈均匀分布。因此,该算法能够有效地防止统计分析的攻击。
五、安全性分析
1、像素的相关性分析
像素的相关性指相邻像素的相似的程度,相关性越大,灰度值的差别越小,图像信息的冗余度也越大。考察相关性,主要方法是考察水平、垂直、对角线相邻像素的相关性。图4显示了明文与密文水平方向的相关性,可见原始图像的相关性很大,本文算法加密后的密文图像的相邻像素的相关性呈现随机的对应关系。

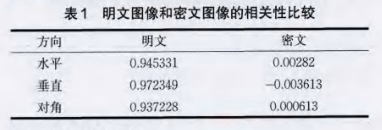
相关系数又称皮(尔生)氏积矩相关系数,能够说明两个现象之间相关关系密切程度的统计分析指标。从原始图像和加密后的图像的水平、垂直及对角方向取lOOO对像素对,根据式(11)进行相关系数计算。

式中,xi,yi分别表示图像中第i组相邻像素的像素值,N为像素对的组数,r为相邻两个像素的相关系数d如下表1所示,原始图像lena的像素存在高度的相关性,r接近于1,对应的密文图像的相关系数r接近于0,基本不存在相关性。表明本文的加密算法能够有效地掩盖原始图像的统计特征。
2、时间效率分析
本算法的仿真实验在Matlab 7.1的实验平台上进行,实验所使用的硬件环境为Intel酷睿i3 3220CPU,3.3GHz主频,2GB内存,120G硬盘口使用本文算法加密一幅256x256的灰度图像的平均时间为47ms,加密算法的速度比较高。
3、密钥的敏感性分析
本算法选取256x256的8位经典测试图像lena.bmp进行测试,2D-Arnold映射的参数a=M-2和b=M—4,置换轮数m=16,超混沌系统初值(x,y,z,w)=(0.22,0.57,1.O,0.30)作为密钥进行加密,然后对超混沌的初值进行微小的扰动(x,y,z,w)=(0.22+10也,0.57,1.0,0.30)生成的密钥进行解密。原始图像和密钥微小扰动之后的解密的图像如图5所示,解密后图像与原始图像存在巨大差别。均方误差MSE可以度量原始图像和解密图像之间的差别,其表达式为:
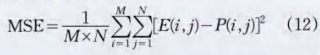
这里,P={P(i,j},E=e(i,j)),i=1,2,..,M,j=l,2,…,N 。 P表示原始图像,E表示解密图像。
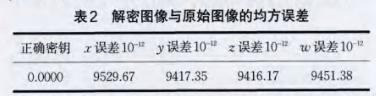
表2给出了本文算法的正确密钥及错误密钥所得的解密图像分别与原始图像之间的均方误差值,使用正确密钥解密,解密图像与原始图像的均方误差为O.OOOO,在其他解密钥保持不变,超混沌方程的4个初值x,y,z,w分别与正确值相差10-12,结果显示,正确密钥可以完全解密,而具有微小扰动的密钥的解密图像与原始图像差别巨大,表明本算法对解密密钥非常敏感。
小知识之映射
映射,或者射影,在数学及相关的领域经常等同于函数。 基于此,部分映射就相当于部分函数,而完全映射相当于完全函数。




