参数可变的离散混沌加密系统

近年来，混沌理论被不同的领域广泛研究，如物理学、数学、经济学和气象科学。混沌系统具有对初值和系统参数的敏感性以及轨道的不确定性，这些特性使得混沌系统对于构造密码系统是一个很好的选择，并且使离散混沌加密系统抵抗统计分析攻击具有鲁棒性。目前提出了很多基于离散混沌映射的加密系统，相应地也出现了大量分析混沌密码系统的方法。混沌密码系统得到大家的广泛研究，其中用得比较多的就是基于Logistic映射的混沌密码系统，一般属于分组加密算法范畴。

Logistic映射被公认为是能体现混沌特点的最简单的离散混沌系统映射。它来源于对人口增长模型的研究，可表示为：

其中：xn和μ分别表示迭代映射的初值和系统参数。图1是Logistic映射分岔图。

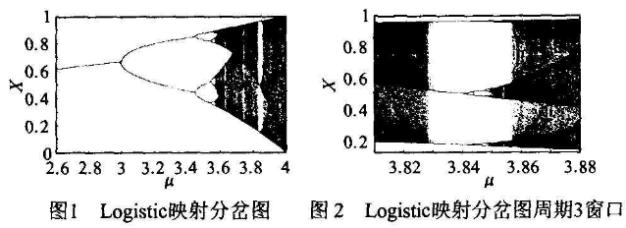
当参数μ超过3时，其解的轨迹出现分岔，而且一分再分，分岔点出现得越来越快，最后成为混沌的一片，出现混沌的系统参数μ=3. 569 945 672…。Logistic映射就是通过这种倍周期分岔过程达到混沌的。将Logistic映射用于密码系统在于它具有三个突出的特性：对初始条件的敏感依赖性、具有伸长和折叠性质、具有内在随机性。这些特性与密码系统的要求是相吻合的。混沌密码系统一般将Logistic映射的初值和系统参数以及迭代次数组合作为密钥。

Logistic映射用于密码系统也遇到一个周期窗口问题。当μ=1+／8=3. 828--到μ=3. 841 037-时，Logistic映射存在周期3解，紧邻接有周期6、周期12等窗口，也相当子一个倍周期化过程d周期3及其邻接的系列窗口如图2所示。关于n周期点的概念简述如下。所谓迭代解代数方程是指：

是否收敛于不动点。迭代解收敛于不动点指：

定义n周期点：

其中：1周期点f(x*）=x*；2周期点f2（x*)=ff(x*)=x*，f(x*）≠x*；3周期点f3(x*）=x*，f2(x*）≠x*，f(x*）≠x*。

当然，要得到n周期点对应的μ值还要加上稳定边界才能实现。

对于使用周期窗口加密一定要慎重，它有可能泄露用户的密钥。例如当μ=3.830和μ = 3. 835时，通过对X0进行多次迭代，最后X0都是(0. 504 666--，O.957 416…，0.156 149---)和(0. 494 514--，0.958634…，0.1520749...)，后面再进行迭代也只会出现这三个值，这是典型的短周期。特别是μ序列已知时更是危险。为了克服这个问题，本文提出了如下的一种基于参数动态变化的新离散混沌密码算法。

一、本文提出的算法

在本算法中，将最大128 bit的变长密钥分成以8 bit为单位的块：

明文／密文被分成多个以8 bit为单位的块：

变长密钥的每一块分别与π的小数部分异或，更新后的密钥变为固定的128 bit密钥，便于后面的计算：

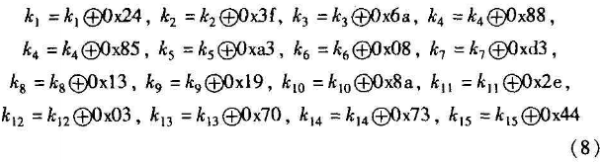
更新后的128 bit的密钥分成以8 bit为单位的块和32 bit为单位的块，分别称为会话密钥和子密钥：

其中kj≠0，j=1，…，16主要是为了避免弱密钥。下面是构造小数Xr，它是混沌映射初值的主要部分4为了充分置乱密钥，保证混沌映射初值有更大的取值空间，把它构造成由两部分组成，分别是Xb1和Xb2，这两者平均都有2的56次方个取值。模i是为了取得纯小数：

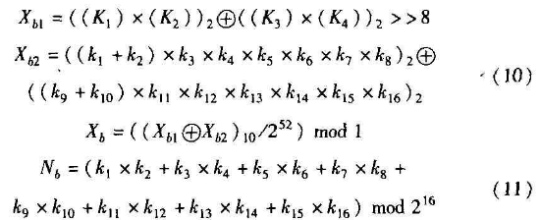
考虑到运算速度和取值空间的均衡，混沌映射迭代次数的主要部分Nb的取值空间构造成2的16次方。

式(9)、(10)中的（）2和（）10分别是数的二进制和十进制表示法。由随机数发生器来动态产生混沌映射系统参数μi、j：

混沌映射初值X和迭代次数N：

其中：kj是自由选择的子密钥；j决定了它在密钥中的顺序；yo =0。一个8 bit的明文／密文分组被加／解密，用初值X和系统一数μi使混沌映射迭代N次。迭代后的新值X( Xi)被用于构造明文／密文。加／解密过程如下所示：

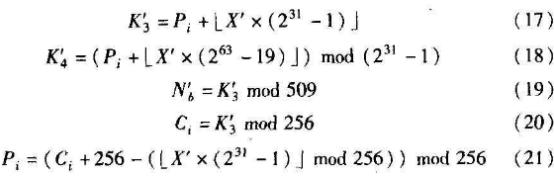
对于加／解密的下一块明文／密文，上一次的X'和Nb'分别代替式(15)(16)中的Xb和Nb，K'3和K'4分别更新式(14)中的随机发生器参数K3和K4。由于Logistic映射系统参数雎随着加／解密过程不断变化，即使系统参数地进入周期3窗口以及紧邻周期3窗口的所有周期窗口都不会出现前述的短周期问题。加／解密过程惟一不同的就是分别使用式(20)(21)得到相应密文／明文。

二、加密算法说明

式(12)(14)是用线性同余随机数发生器来产生Logistic混沌映射的系统参数d，已论证了随机数发生器中乘法器和模的取值问题，由于在式(12) C14)中乘法器是由密钥分离而来。可以不考虑它的取值问题。在式( 14)中模取231 -1，因为它是一个奇素数，产生的随机数具有比较大的周期。由于双精度占64位（其中第1位是符号位；依次是指数位，占11位；剩余的52位是尾数），本文取252作为式(12)的模是恰当的，充分保证了系统参数以的密钥取值空间，又不会引入小数的不确定位。

算法中的输出反馈是必不可少的，它动态地改变了混沌映射初值、迭代次数以及线性同余随机数发生器参数，明文中任意字符均会影响到其后字符对应的密文，加强了算法的安全性。

三、实验结果和安全性分析

采用以下实验环境：CPU是Intel Celeron处理器，主频450MHz；内存192 MB；操作系统Windows 2000；使用VC++编程实现本文的算法。

表1表示使用密钥“317879323365666761343536377 A7463”对明文“chaotic”进行加密的过程。整数类型用的是signed—int64，小数类型用的是long double。如果小数类型采用single将使密码空间降低约1倍。算法设计的目的是使Logistic映射的系统参数、初值和迭代后的值分别平均约有2的52个取值。

1、统计分析

图3表示加密过程使用的22 KB文本文件的明文分布。

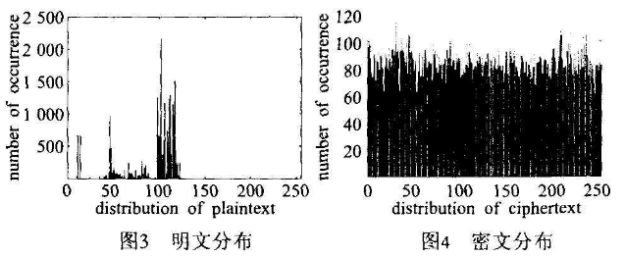
图4表示本算法加密后22k文件的密文分布，扩展密钥用的是”317879323365666761343536377 A7463”。很明显，明文是一些高频字符，经过加密后密文分布却是平坦的象Shannon曾说过，统计分析经常被用来进行密码分析和破译，好的密码系统不管明文是如何分布的但密文分布应该是均匀的。

从图4的密文分布完全能说明本文的算法能有效防止密码分析者利用统计分析的方法来击破整个加密系统。

2、敏感性测试

Shannon指出，一个好的加密系统，它的函数必须是复杂的，并且一个小的变化必然导致结果发生很大的变化。图6、7表示对图5明文用仅差一位的密钥加密后所得的结果，使用的密钥分别是“317879323365666761343536377A7463”和“117879323365666761343536377A7463”。从图中不难看出，虽然密钥仅仅相差一位，但加密后所得的密文却完全不同，这也说明本文所设计的密码系统对密钥具有敏感性。图8是用图5明文变化一个字符，将其最前面字符“A”变为“a”，密钥仍然使片“317879323365666761343536377 A7463”得到的密文比较图6、8的密义，可以看出两者完全不同，很明显对明文是敏感的。本文算法表现出的对密钥和明文的敏感性是与Shannon提倡的好密码系统相吻合的。

3、抵抗各种攻击分析

比较典型的穷举攻击方法有：

a）惟密文攻击( ciphertext only attack)。密码分析者仅知道一些密文，而对明文一无所知。这种攻击手段是所需信息最少的，也是难度最高的手段之一。

b）已知明文攻击( known plaintext attack)。密码分析者知道一些密文以及对应明文，但不知道密钥。在这种情况下，如果密文和明文具有比较确定的对应关系的话，密码分析者就很容易通过替换、查找、类推、猜测等手段破译密文。

c）选择明文攻击( choscn plaintext attack)。密码分析者能够临时访问加密机，因此能够任意选择一个明文字符串，并可构造相应的密文字符串，一个密码系统比较容易受到这类攻击。

d）选择密文攻击( chosen c:iphertext attack)。密码分析者能够临时访问解密机，因此能够任意选择一个密文字符串，并可构造相应的明文字符串，一个密码系统比较容易受到这类攻击弘很显然如果密文能够抵抗选择明文攻击，则足以抵抗其他各种攻击。根据著名的Kerchoffs准则，本文假定密码分析者知晓除密钥以外的所有事情矗在本文提出的算法中，通过输入反馈的方式，后面输入的密文都与前面加密的明文相关，密码分析者不可能得到与明文无关的密钥流。加上使用的Logistic映射的系统参数、初值和迭代后的值分别平均都约有252个取值，迭代次数取值空间平均约为2的9次方，因此每一步迭代的密钥空间约为2的9次方；密钥空间非常大奠在目前的计算条件下，密码分析者通过选择一些明文和相应密文来穷举子密钥是非常闲难的，而在算法中整个密钥空间为2的128次方，要想恢复出整个密钥更是难上加难。